正交试验设计的岩质路堑植被边坡稳定参数敏感性分析

王喜华，赵志明，吴 光

(1.西南石油大学资源与环境学院，四川成都 610500;2.西南交通大学地球科学与环境工程学院，四川成都 610031)

1 岩质路堑植被边坡的稳定性

近年来，随着我国西部大开发战略的实施，在大量铁路、公路等工程项目的施工中，不可避免地遇到大量岩质路堑边坡。对于这些工程边坡，除了采取必要的支挡措施保证边坡的稳定外，还应尽量对稳定的岩质路堑边坡绿色防护层的稳定性作进一步的研究，以有效快速地恢复破坏了的自然环境。

影响岩质路堑边坡表层土稳定性的因素很多，主要体现在表层土的抗剪强度指标、表层土的厚度、表层土的重度、岩质路堑边坡的坡度、地下水水位高度、降雨特征、地震作用以及人为因素等。但每种因素对表层土的影响程度各异，大小不一，这些影响因素有的是确定性的，但大部分具有随机性、模糊性、可变性等不确定特点。

本文结合渝怀(重庆至湖南怀化)铁路鱼嘴车站岩质路堑植被边坡的绿色防护工程，基于正交试验设计原理进行其稳定参数的敏感性分析。

2 正交试验设计方法

所谓正交试验设计，就是一种处理多因素试验的科学试验方法。它可利用一种规格化的正交表，合理安排试验，用这种方法只需较少次数的试验便可判断出较优的条件，对试验结果进行简单的统计分析，就可以做出正确的判断。正交试验设计方法能明确回答以下问题:①因素的主次，即各因素对所考察指标影响的大小顺序;②因素与指标的关系，即每个因素水平不同时，指标是如何变化的。该方法主要包括正交试验设计和正交试验结果分析两方面的内容。

通过建立的岩质路堑边坡表层土稳定计算的模型，计算其稳定安全系数Fs，稳定因素的影响表现为不同水平计算参数所获得的表层土的安全系数。

为了分析表层土稳定影响因素的敏感性，对以Fs为评价对象的单指标多因素进行显著性分析。

单指标多因素的显著性分析可采用线性模型如下

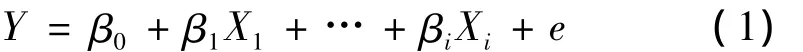
式中，β0为常数项;βi为自变量;Xi为回归系数;e为随机误差，服从标准正态分布。

如果在模型中令某些因素的主效应或交互效应为零，而其余效应的最小二乘估计不受影响，即与在不假定上述效应为零时所得的估计一致。这保证对每个效应的估计不受到其他效应的影响。则设计矩阵X必须满足如下条件

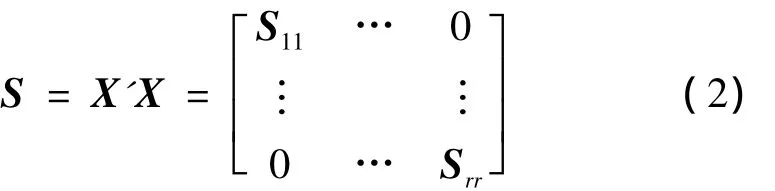
式中，S11，S22，…，Srr都是方阵，每一块相应于一组效应。

对于某个因素变量Xi对指标Y的显著性次序分析，不要求做定量结论，只要求辨明Xi对因变量Y的显著性影响次序。因此无须求解式(1)中的回归系数，只需按式(2)设计试验。

此时，正交试验可满足模型要求。设A，B，…表示不同的因素，r为各因素水平数，Ai表示因素A的第i水平(i=1，2，…，r)，Xij表示因素 j的第 i水平的值(i=1，2，…，r;j=A，B，… )。在 Xij下进行试验得到因素j第i水平的试验结果指标Yij，Yij是服从正态分布的随机变量。在Xij下做了n次试验得到n个试验结果，分别为 Yijk(k=1，2，…，n)，则计算参数如下

在这一话题的新闻语篇中，媒体闭口不谈巴黎协定给欧洲带来的经济效益，而把话题锁定在人类生存的角度，在语篇中出现频次最多的是人类架构，受众在阅读报道时能够反复激活与人类相关的架构，从而将保护环境和人类生存建立直观的联系；在报道中反复出现的战争架构(protect、defend)和犯罪架构(accuse)强化了 “保护环境需要人们积极抗争”等深层价值观，并将退出巴黎协定的行为置于受众的对立面，激活了“犯罪是不道德的”“威胁人类生存是不道德的”“与全人类为敌是不道德的”等心理架构，引起广泛的民意反对。

式中，Kij为第j因素在第i水平下的统计参数;n为第j因素在第i水平下的试验次数;Yijk为第j因素在第i水平下第k个试验结果指标值。

评价因素显著性的参数为极差Rj，计算公式为

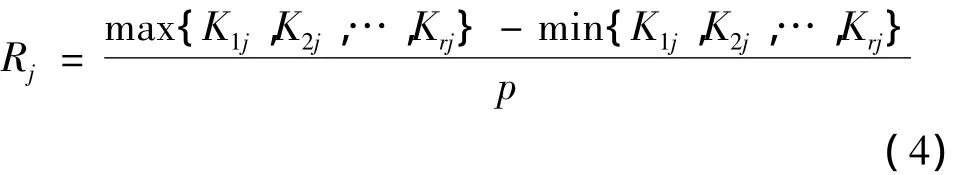
式中，p为参加试验因素的水平数。

极差分析法可得出各因素对试验指标影响的相对大小，极差越大说明该因素的水平改变对试验结果的影响也越大，极差最大的因素也就是最主要的因素，极差较小的因素为较次要的因素，依次类推。所以根据极差大小可判断因素的主次。

3 实例分析

3.1 渝怀铁路鱼嘴车站岩质边坡工程概况

渝怀铁路(重庆至湖南怀化)是我国西部大开发中基础设施建设的标志性工程之一，由重庆枢纽段和正线两部分组成。

鱼嘴车站处为丘陵沟槽地貌，自然坡度10°～30°，海拔 180～260m。覆盖层为第四系坡洪积()、坡残积)、下伏基岩侏罗系中统沙溪庙组(J2s)。线路位于DK51+602与广福寺向斜70°斜交，岩层以泥岩为主，节理不发育。地表水为水塘中水，由大气降雨补给，地下水不发育。测段无不良地质现象，地层岩性主要为软土。绿化效果见图1。

图1 鱼嘴车站喷射厚层基材植草护坡效果

3.2 岩质路堑边坡表层土稳定计算模型

现只讨论一坡到顶式边坡计算模型，则边坡表层土的受力如图2。

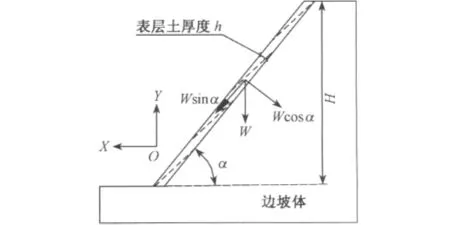
图2 一坡到顶式边坡计算模型

稳定系数可以用Fs表示，即

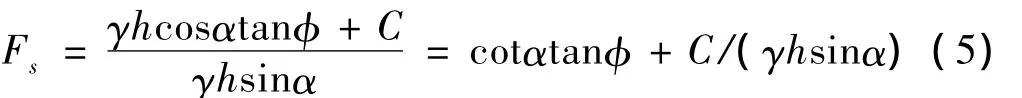
式中，C为表层土黏聚力(kPa/m);φ为表层土内摩擦角(°);γ为表层土重度(kN/m3);α为边坡坡度(°);h为表层土厚度(m)。式(5)对有根系边坡和无根系边坡都是适用的，由于根系对边坡的加筋作用，黏聚力C提高，φ也有所增大。

3.3 各影响因素的敏感性分析

影响边坡表层土稳定的因素很多，主要有坡度α，表层土厚度h，表层土的重度γ及其力学参数C，φ值。以下进行各影响因素的敏感性分析。

参数取值范围按照地勘等资料确定，并将其概化为高、中、低三个因素水平。为了减少由于水平次序引起的系统误差。各因素水平的次序应随机排列。参数取值范围及因素水平次序如表1所示。

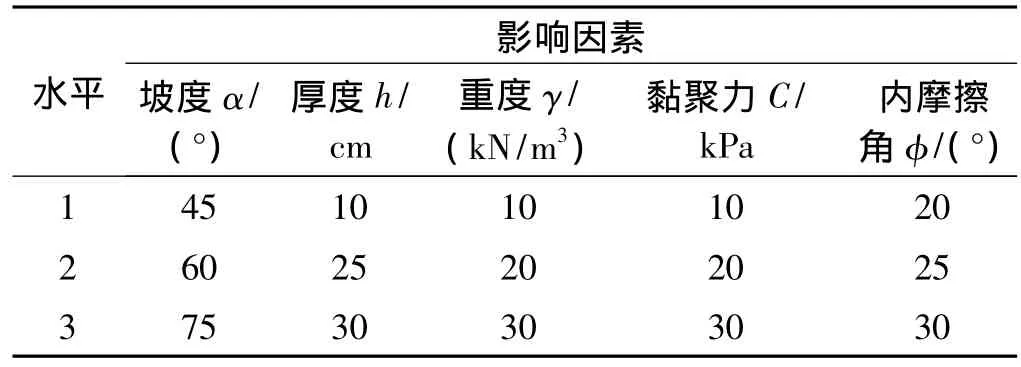
表1 各影响因素取值范围及水平

3.4 正交试验结果与分析

根据确定的影响因素，本文将进行5因素3水平的试验分析。采用正交试验法，不考虑因素间的相互作用，可选用正交表L18(37)，试验次数为18次，是全面试验的7.4%。将各因素排在正交表前5列，剩余两个空白列为误差列。

按照表2确定的试验方案，采用式(5)对一坡到顶的岩质路堑边坡表层土体进行以稳定安全系数为指标的多因素显著性计算分析。正交试验因素水平概化值及计算结果见表2。

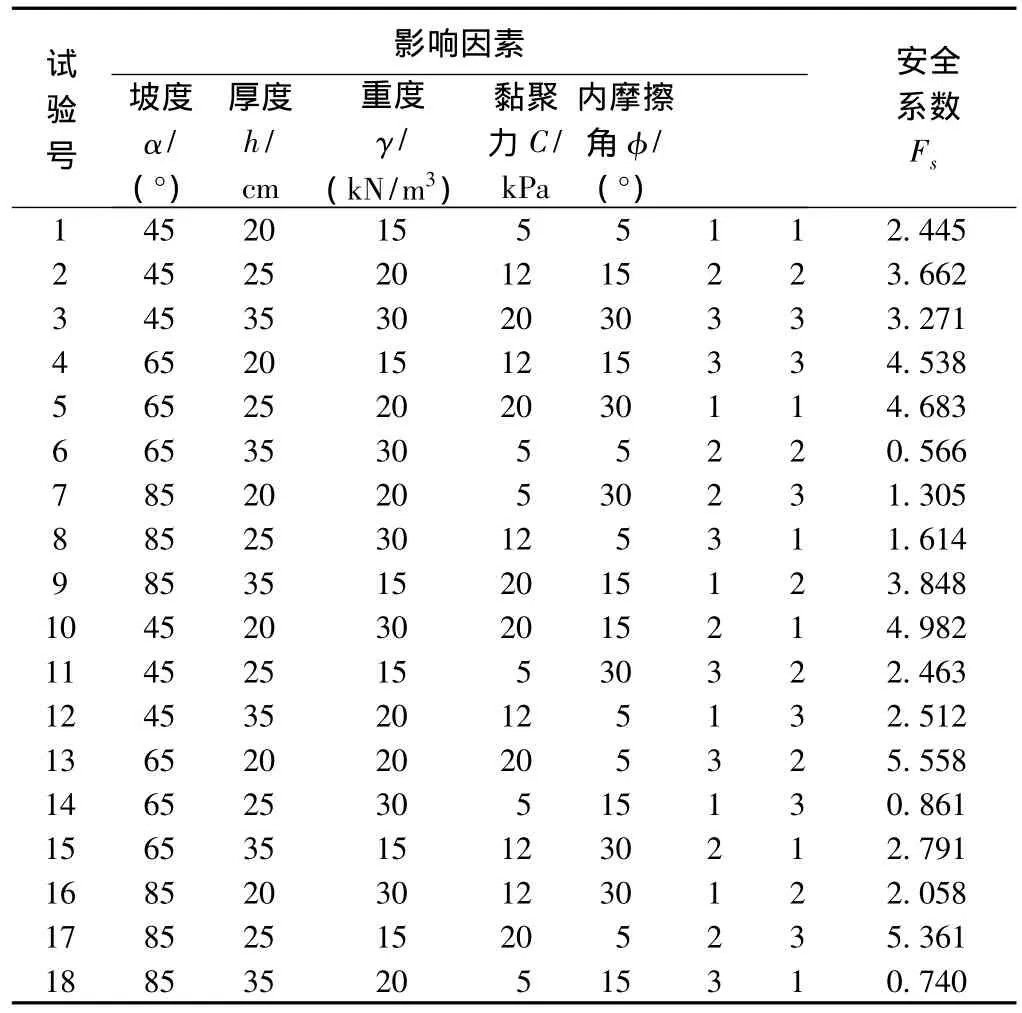
表2 正交试验计算结果

3.4.1 极差分析

对正交试验结果进行极差分析，分析结果如表3。由表3可知，影响表层土稳定性的5个因素中，参数敏感性由大到小依次为C＞γ＞h＞α＞φ。

因指标值安全系数要求取较大者，因此各因素的最优水平为 1，1，2，3，2。

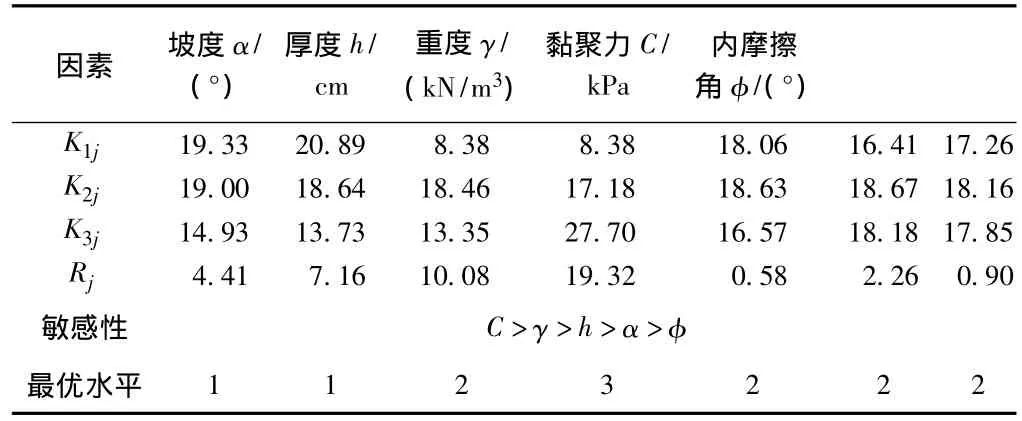
表3 各参数极差分析

3.4.2 趋势图分析

趋势图分析法又叫比较分析法、水平分析法，是因素与指标关系趋势分析法，即计算因素各个水平的平均试验指标，以因素的水平为横坐标，以平均指标为纵坐标，绘制因素—指标关系趋势图，然后找出各因素水平与试验指标的变化规律。

根据表3作各因素的趋势分析图如图3所示，其中横坐标为各因素分类，其水平值按次序排列，纵坐标为反映稳定性系数Fs大小的统计参数Kij。由图3可以看出:Fs随C、γ、h变化且变化较大;Fs随α，φ的变化不明显。

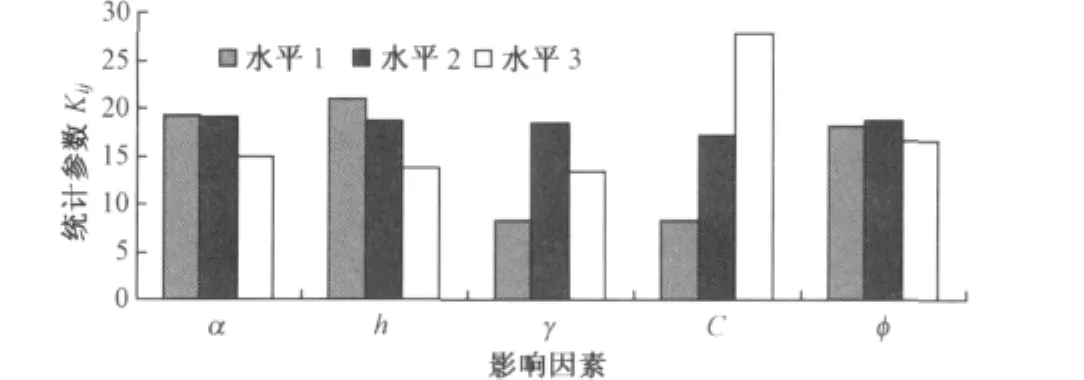
图3 各影响因素的趋势分析

4 结论

1)运用正交试验设计方法对渝怀铁路鱼嘴车站岩质路堑边坡表层土稳定性影响因素进行敏感性分析，结果表明所选取的5个影响因素的敏感性由大到小依次为:黏聚力C＞表层土重度γ＞表层土厚度h＞边坡坡度α＞表层土内摩擦角φ。

2)Fs随C，γ，h 变化且变化较大;Fs随 α，φ 的变化不明显。

3)正交试验设计方法用于岩质路堑边坡表层土稳定性影响因素敏感性分析，综合考虑了影响其稳定性的多种因素，该方法可行、合理，结果可靠，可以在工程实践中推广使用。

［1］倪恒，刘佑荣，龙治国.正交设计在滑坡敏感性分析中的应用［J］.岩石力学与工程学报，2002，21(7):989-992.

［2］张万涛，余宏明.正交试验设计方法在库岸滑坡敏感性分析中的应用［J］.安全与环境工程，2009，16(5):13-16.

［3］刘海燕.应用概率论与数理统计(下册)［M］.成都:成都科技大学出版社，1997:74-107.

［4］王辉，李莉.高边坡锚固参数敏感度分析［J］.公路，2006(4):165-167.

［5］夏雄，周德培，王利平，等.锚固边坡稳定性因素敏感度分析［J］.常州工学院学报，2008(21):99-102.

［6］李扬，杨继红，刘汉东.岩体结构控制下的边坡稳定性多因素敏感性分析［J］.铁道建筑，2011(1):88-90.

［7］张健，孙巧根，长铮.基于正交试验的方法分析边坡稳定性影响因素的显著性［J］.中外公路，2005，25(5):8-11.