350 km/h高速铁路路桥过渡段动力响应分析

2012-09-05杨长卫

铁道建筑 2012年10期

陈琪，杨长卫

(1.西南交通大学高速铁路线路工程教育部重点实验室，四川成都 610031;2.西南交通大学土木工程学院，四川成都 610031)

高速铁路设计中线路的平顺性是保证高速列车安全、可靠、舒适运行的前提。在整个线路中，路桥过渡段对整个线路的平顺性具有显著影响，成为影响整个线路平顺性的主控因素之一。当高速列车通过该区段时，由于桥台和路基两部分存在较大的刚度差，造成该处出现较大的工后沉降差，致使轨面在此处出现弯折现象，破坏了轨道的平顺性，加速了线路状态的恶化，降低结构的使用寿命，影响列车的舒适度，甚至会造成列车失稳现象的发生。因此，有必要开展高速列车荷载作用下路桥过渡段部分动力响应的研究。

为了更加详细地揭示列车荷载作用下高速铁路路桥过渡段的动力响应，本文选取典型工况点，结合现场实测数据，利用有限元软件，建立三维数值分析模型，施加350 km/h的高速列车荷载，分析了路桥过渡段的动力响应。

1 数值分析

1.1 数值计算模型

本文运用有限元软件MIDAS/GTS，依据《京沪线高速铁路设计暂行规定》，以京沪客运专线某一工况点为原型，建立倒梯形路桥过渡段的数值模型。过渡段的几何尺寸如下:基床表层厚0.6 m，基床底层厚1.9 m，路堤填土厚6 m，桥台长27 m，轨枕采用标准规格，轨距1 435mm。过渡段采用正梯形设置，梯形上边长6 m，斜边坡比为1∶2，填筑材料为掺一定量水泥的级配碎石。MIDAS/GTS存在实体和构件两种建模方式，为了尽可能真实模拟路桥过渡段各个部分的力学性能，本文采用实体建模。桥台与碎石土、轨道板与基床表层之间通过设置接触单元来模拟其相互作用。为了研究的方便，本文对该工况点做了相关简化，具体数值模型见图1。

图1 数值计算模型轴视图

1.2 参数选取

为了模拟列车荷载，本文采用ADAMS/Rail进行仿真计算，得出列车轮载的时程曲线，见图2。

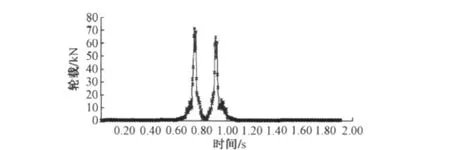
图2 列车轮载的时程曲线

基床表层、基床底层、路基本体的力学特性参数主要通过开展一系列土工试验测得，地基的力学特性参数主要通过前期的地质勘察获得。桥台部分由于材料性质较好，预计变形很小，因此采用线弹性本构模型;过渡段碎石、路基土、基床表层、基床底层均采用Mohr-Coulomb模型，土体的具体力学特性参数见表1。

表1 土体物理特性参数

本文通过在模型两侧和底部设置黏弹性边界来消除边界反射的振动对过渡段动力响应的影响。该边界所需计算参数的求解依据以下公式:

式中，Av，Ah为各个地基的竖向和水平方向的截面面积，E0为地基的弹性模量，α取1.0，边界特性参数见表2。

表2 边界特性参数

2 计算结果

本节所涉及的钢轨表面竖向转角是指发生于钢轨所在平面内的转角。

为了研究列车荷载作用下路桥过渡段动力响应沿其纵向的分布情况，本文测点分布如下:首先在桥台端部设置一个测点，台后0.75m，1.5m处各设置一个测点，之后再设置17个测点，间距均为1.5m，测点全部位于基床表层和轨面。

为了研究列车荷载作用下路桥过渡段动力响应沿其横向的分布情况，本文测点分布如下:首先在桥台后10.5m处沿轨枕中心线两侧0.5m，0.75m，0.75m，0.5m分别设置动应力观测点;在桥台后7.5m处沿基床表层中心线布置沉降观测点。

由图3可知，过渡段的最大沉降量6.436 mm发生于桥台后约7.5m，台后10m以外沉降基本上稳定于6.0mm左右。研究还表明，轨面的最大弯折角2.67‰发生于桥台后约1.5m处。在桥台后10m以后的范围内，轨面转角基本上稳定在约0.3‰以下。路桥过渡段出现这种现象主要是由于路桥连接处存在较大的刚度差，造成列车下桥时车轮会产生一个向下的附加冲击作用，从而加大了该处的竖向变形。