随机有限元法在桥梁地震随机响应分析中的应用

陈 兵，廖光明，王遂泸，龚 铖，陈思孝

(1.四川大学建筑与环境学院，四川成都 610065;2.四川蜀渝石油建筑安装工程有限公司，四川成都 610017;3.中国中铁二院工程集团有限责任公司土木建筑设计研究二院，四川成都 610031)

地震作用下桥跨结构响应的随机性主要源于两方面:结构参数的随机性和地震激励的随机性。对于确定性线性结构在随机激励作用下的响应——随机振动研究，已经有了较为成熟的分析方法［1］。在结构参数静力分析以及稳定性分析的随机性响应方面，也取得了较大的进展［2］。近年来，关于具有随机参数的结构受随机激励的动力响应分析——双随机问题或复合随机问题，日益受到重视，并且逐渐出现了一些研究方法。如Igusa和Kiureghian假定结构参数的随机分布概率密度已知，将结构的随机响应归结为可靠度分析并用近似的方法计算了概率积分［3］，但该方法较为复杂，不便于工程应用;Lee和Singh将激励的幅值作为随机变量，研究了参数随机结构的响应问题［4］，但其激励的时间变化规律还是确定性的，不能算作通常意义上的随机激励。

目前理论上较为成熟的随机结构分析方法主要有Monte Carlo随机模拟法、随机参数摄动法和随机有限元方法。Monte Carlo数值模拟法随着所取样本数的增加，理论上可以达到任意高的精度，但即使对于简单结构，也要花费大量计算时间，计算效率比较低，一般用来评估计算方法的精度，在实际工程设计中应用较少。随机参数摄动法是在确定性参数摄动法基础上发展起来的，最初用于解决动力特征值问题，后来拓展到动态响应问题。随机有限元方法是在传统有限元方法基础上发展起来的随机数值分析方法，是随机分析理论与有限元方法相结合的产物，能较为有效地解决具有随机参数的结构受随机激励的动力响应分析问题，在岩土工程、复合材料、水工非杆系混凝土结构工程设计及可靠性分析等领域得到了一些应用［5-7］，然而，随机有限元法在桥梁等复杂结构地震随机响应分析方面的研究和应用成果还很少。本文应用随机有限元方法，采用程序开发工具C++Builder编制了能分析计算具有随机参数的桥梁结构在随机地震激励下的响应程序，计算了一座高墩大跨连续刚构桥梁的随机动力响应。

1 随机有限元方法

采用随机有限元方法分析具有随机参数的桥跨结构在随机地震激励下的动力响应，主要涉及到随机场的离散和随机有限元动力方程的建立及求解两个方面的问题。

1.1 随机场的离散

1.1.1 局部平均随机场

桥梁结构系统参数不确定性可以用随空间分布的随机场或随时间分布的随机过程加以描述。随机场的空间离散方法主要有:中点离散法、局部平均法、形函数插值法、最优线性估值法、局部积分法等。局部平均法对原始数据要求较低、收敛快、精度较高，是较为常用的随机场离散方法［8］。对于一维和二维的连续平稳随机场，局部平均理论可以比较方便地描述其随机特性，故本文采用局部平均理论和文献［9］提出的“空间杆系分离随机场模型”来离散桥梁结构参数的随机场。“空间杆系分离随机场模型”将空间三维随机场简化为仅沿杆件长度方向分布的一维均匀随机场，在杆件长度方向不重合的杆件之间，其随机场彼此无关，相关函数可表示为

不同长度方向杆件的一维随机场就构成了结构的空间杆系分离随机场模型，每个分离的一维随机场都采用局部平均理论描述。

根据随机有限元理论，随机变量在任意两个长度分别为Ti和Tj单元上的局部平均随机场分别为［10］

这两个随机场单元的几何尺寸如图1所示。

图1 一维局部平均单元

它们之间的协方差为

式中，σ2为原随机场方差，γ(T)为方差函数，可按文献［11］建议的近似公式式(4)计算

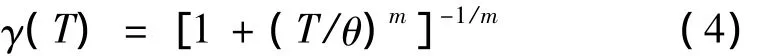
式中，θ为相关偏度，可按式(5)计算［12］∞

式中，ρ(τ)为随机场的相关函数。

1.1.2 有效正交随机变量

按局部平均处理的随机场的离散化随机变量{α}的协方差矩阵B=［cov(αi，αj)］一般是N×N阶满秩矩阵，计算量较大，给随机分析带来不便。为了减少计算量，可以利用随机变量的特征正交化方法［10］，将其转换为对角的方差矩阵Λ =［Var(βi)］，其中{β}为一N维分量互不相关的构造随机向量。

由随机向量协方差的性质可知，其协方差矩阵B为对称正定阵，因此必然存在一个正交矩阵Φ，使得B与对角阵Λ相似

其中Λ的对角元素为协方差矩阵B的特征值，Φ的列向量为对应的特征向量。构造一个相互独立的随机向量{β}，使其满足

式中B'为{β}的近似协方差矩阵，‖B‖、‖B'‖为协方差阵B和B'的范数。给定误差限δ后，由式(9)迭代即可求出保证计算精度所需随机变量{β}的元素个数n。

1.2 随机有限元法列式

1.2.1 随机有限元动力方程

随机参数结构的动力方程按随机变分原理表示为

式中，ci为对角阵Λ中对角元素，也就是协方差矩阵B的特征值。则{α}与{β}的转换关系可表示为

用相互独立的随机向量{β}代替{α}后，随机有限元的计算量将大为降低。实际上，只要取{β}中部分分量就可以近似表征 {α}。用{β}=(β1，β2，…，βn)近似替代 {α}=(α1，α2，…，αN)(n ＜ N)后，协方差矩阵的误差可用式(1)估计

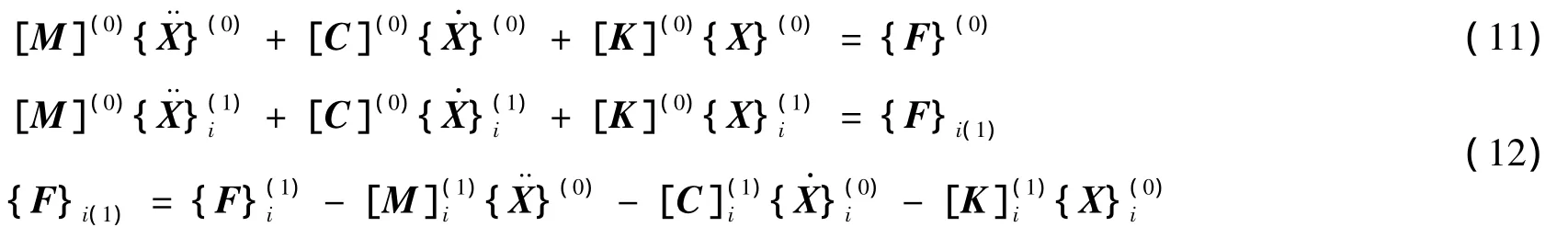
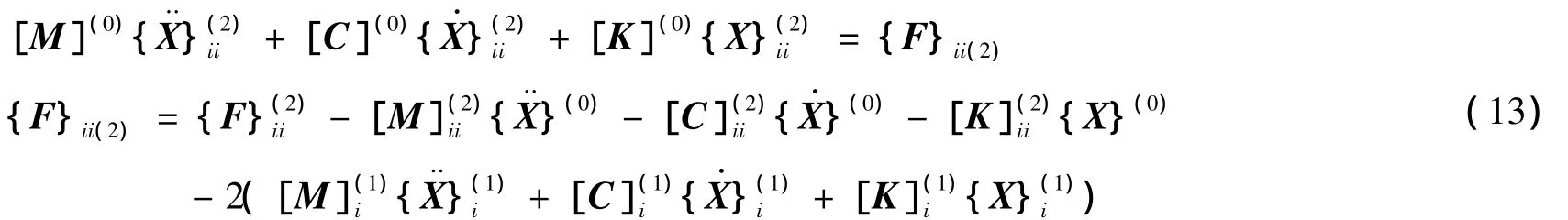
求解方程(11)～(13)，即可得出结构动力响应具有二阶精度的均值为［·］i表示对随机变量βi求偏导数。

与确定性结构的动力方程相比，随机有限元法多了一阶和二阶变异方程，零阶方程与之相同，且递推方程等式左边的矩阵［M］(0)、［C］(0)和［K］(0)与确定结构的动力方程中对应项相同。

按随机有限元方法得出的零阶、一阶和二阶变异方程实际上已经变成确定性的递推方程组，故可采用结构动力学中各种确定性方程的解法求解。对于多自由度体系，一般用时域内的直接积分法，如Wilson-θ法或频域内的振型叠加法求解。

1.2.2 地震激励的随机性

在平稳随机地震作用下，随机参数结构的动力方程式(10)右端地震激励可表示为

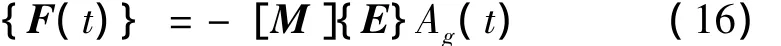
式中，{E}为由0和1构成的惯性指标向量，Ag(t)为地面运动加速度。因此，随机地震动响应的各阶荷载项为

具有一阶精度的方差为

式(11)～(15)中，［·］(0)、［·］(1)及［·］(2)分别为对应于随机变量{β}的均值处的零阶、一阶和二阶变异量，

将(17)式带入随机结构动力有限元分析的零阶、一阶和二阶递推方程的式(11)～式(13)，即可解出随机结构动力响应具有二阶精度的均值和具有一阶精度的方差。

2 算例

2.1 方法验证

为了验证本文所运用理论及编制程序的正确性和有效性，分别采用随机有限元法和Monte Carlo方法计算了图2所示具有随机参数的悬臂梁在随机地震激励下的响应。悬臂梁长L=1.0m，横截面积A=1×10-4m2，扭转惯矩J=1.41×10-7m4，弯曲惯矩Iy=Iz=8.3×10-6m4，弹性模量 E=2.1×1011Pa，泊松比 μ=0.3，随机质量密度ρ=7 800 kg/m3，假定服从高斯分布，变异系数为0.1，地震激励时程为El Centro波，加速度峰值0.5g，加速度放大系数的变异系数0.1。采用Monte Carlo的Latin Hypercube抽样方法，样本数为2 000，时间步长0.02 s。随机有限元局部平均单元取10个，有效随机变量5个，各阶递推方程采用Wilson-θ求解。悬臂端11号节点在0～1 s时间内y方向位移响应的均值计算结果见图3。

从图3可以看出，随机有限元方法的计算结果与Monte Carlo方法结果吻合得较好，说明本文编制的随机有限元程序是正确的。

2.2 应用实例

襄渝铁路增建二线牛角坪双线特大桥(图4)，是目前国内跨度最大的预应力混凝土连续刚构铁路桥，其孔跨布置为(118+192+118)m，仅次于世界最大跨度的葡萄牙坡托桥(主跨250m)。主要材料参数为［14］:梁体混凝土强度等级 C55，弹性模量3.6×104MPa，重度26.5 kN/m3;空心墩混凝土强度等级C35，弹模3.3×104MPa，重度25.0 kN/m3，岩石地基为弱风化凝灰质砂岩，线路设备及道砟自重等二期恒载取130 kN/m。该桥位于Ⅵ度地震区，设计地震动峰值加速度为0.05g，g为重力加速度。本文采用Hollywood Storage地震时程记录，其动峰值加速度0.059 2g(图5)。桥梁结构参数随机性考虑了主梁截面积、混凝土弹性模量、质量以及二期恒载重量的不确定性，地震的随机性由式(16)计算。

桥梁中跨跨中平稳地震响应具有二阶精度的均值计算结果见图6和图7，其余计算结果未予列出。

3 结语

结构参数和地震激励的随机变异性对结构的响应有很大影响，通常，结构最大响应的变异系数大致是结构参数变异系数的2～4倍，有的文献给出的算例高达7倍［15］，桥梁计算分析中应当考虑它们的影响。

本文根据随机有限元理论，运用程序开发工具C++Builder编制了能分析计算具有随机参数的桥梁结构在随机地震激励下的响应程序，并通过Monte Carlo方法验证了程序的正确性。最后，对一座具有随机参数的高墩大跨连续刚构桥梁在随机地震激励下的响应做了分析，计算了结构在随机地震激励下中跨跨中的动力响应。

［1］欧进萍，王光远.结构随机振动［M］.北京:高等教育出版社，1998.

［2］赵雷，陈虬.随机有限元动力分析方法的研究进展［J］.力学进展，1999，29(1):9-18.

［3］IGUSA T，KIUREGHIAN A D.Response of Uncertain Systems to Stochastic Excitation ［J］.Journal of Engineering Mechanics，1988，114(5):812-832.

［4］LEE C，SINGH R.Analysis of Discrete Vibratory Systems with Parameter Uncertainties，Part Ⅱ:Impulse Response［J］.Journal of Sound and Vibration，1994，174(3):395-412.

［5］刘幸，方梅，张立军.钢筋混凝土随机有限元理论及在水工非杆系结构中的应用［M］.北京:中国水利水电出版社，2003.

［6］武清玺.结构可靠性分析及随机有限元法［M］.北京:机械工业出版社，2005.

［7］辛亚军，陈普，程树良.基于ANSYS有限元简化模型的斜拉桥地震响应分析［J］.铁道建筑，2010(9):37-40.

［8］朱位秋，任永坚.随机场的局部平均与随机有限元［J］.航空学报，1986，7(6):604-611.

［9］CHEN Qiu，ZHAO Lei.Stochastic Seismic Response Analysis of Concrete Frame Structures with Random Parameters by Taylor Expansion［J］.J.Southeast Unvi.(English Edition)，1995，11(1):355-360.

［10］陈虬，刘先斌.随机有限元法及其工程应用［M］.成都:西南交通大学出版社，1993.

［11］VANMARCKE E.Random FieldsandstochasticFinite Element［J］.Structural Safety，1986，3(3/4):143-166.

［12］VANMARCKE E.Random Fields:Analysis and Synthesis［M］.Cambridge:The MIT press，1983.

［13］赵雷，陈虬.结构动力分析的随机变分原理及随机有限元法［J］.计算力学学报，1998，15(3):263-274.

［14］中华人民共和国铁道部.TB 10002.3—99 铁路桥涵钢筋混凝土和预应力混凝土结构设计规范［S］.北京:中国铁道出版社，2000.

［15］李杰.结构动力分析的若干发展趋势［J］.世界地震工程，1993(2):1-8.