基于B平面算法的火星探测器中途轨道修正

唐 卫

(上海航天控制技术研究所，上海200233)

基于B平面算法的火星探测器中途轨道修正

唐 卫

(上海航天控制技术研究所，上海200233)

探测器在日心过渡段轨道的轨道修正问题是火星探测工程中需要解决的关键问题.首先，引入B平面坐标系，推导了B平面参数的计算公式，验证了速度修正量与目标参数间存在的线性化关系，给出了算法流程图.其次，在引入合理的速度执行误差与测轨误差的情况下，提出了一个包含三次主修正，一次机动修正，一次备份修正的控制策略，仿真验证了控制策略的可行性.

火星探测;轨道修正;B平面

逃离地球引力场后，星际探测器进入日心过渡轨道.由于在逃逸引力场时不可避免存在变轨误差和定轨误差等，因此需要在日心过渡轨道段进行轨道修正以满足设定的要求[1].20世纪60年代，中途制导计算方法和制导策略的研究得到了许多学者的重视.数值搜索的方法计算量大，不利于轨道控制的分析和实际在轨操作，所以一般采用线性修正的方法.在小偏差情况下，线性方法具有精度足够高，计算耗时少.Kizner发现建立在目标星的B平面参数与轨道状态量的偏差量之间存在着线性关系[2]，而B平面参数很容易转换为目标量，由此可计算得到修正误差所需要的速度冲量，Kizner的工作大大促进了深空轨道制导的研究，行星际飞行轨道修正的目标参数(如轨道倾角，轨道高度)都能够转换为B平面参数.Hintz和Chadwick基于B平面参数给出了一种中途制导轨道修正方法[3]，该方法用参数化数据来满足目标参数约束、定轨误差等因素.本文采用B平面算法进行中途轨道修正，并给出中途轨道控制策略.

1 B平面坐标系

所谓B平面就是包含二体假设下的双曲线轨迹的焦点(对于火星段双曲线轨道，焦点就是火心)，且垂直于双曲线的进入渐近线的平面.B平面和探测器轨道平面相交，在空间得到一条交线.B矢量沿着这条线，以焦点为起点，终点在进入渐近线穿过B平面处.设进入渐近线单位矢量为S，引入行星赤道面法线或黄道面法线单位矢量N，二者叉乘得到垂直于S并穿过行星中心的矢量T:T=S×N，将S和T叉乘可得到矢量R:R=S×T，B平面内B矢量在T和R方向投影，构成了瞄准参数B·T和B·R.其空间几何关系如图1所示.

图1 B平面空间几何Fig.1 Spatial geometry of B-plane

2 轨道控制算法

2.1 由位置矢量r和速度矢量ν计算B矢量

设其轨道面法线单位矢量n，则n=r×ν/|r× ν|，偏心率矢量为:e=ν×h/μ-r/|r|，其中μ为中心星体的引力位常数，h为探测器相对于火心的动量矩，h=r×ν.由于S在探测器轨道平面内，选取轨道平面内两个标准正交的矢量组成一个坐标系，就能唯一确定它的位置，取e为X轴，e和n叉乘为Y轴.设S与e的夹角为θ，飞入渐近线矢量为:S= cosθe+sinθ(n×e)，则:B=b(S×n)，其中b为双曲线短半轴.进一步求得BT和BR:BT=B·T，BR= B·R.

2.2 由轨道要素计算B矢量

下面取B平面的参考平面为火星赤道平面，定义火星近焦点坐标系如图2所示.

图2 火星近焦点坐标系Fig.2 Mars near focus coordinate system

取偏心率单位矢量e为X轴，它以焦点为起点，背向近星体点.n和e叉乘构成Y轴，B矢量和S矢量分别可以表示为:B=b[sinθ -cosθ 0]T，S= [cosθ sinθ 0]T，其中θ=arcos(1/e)，e=1+点赤经为Ω，近火点幅角为ω的目标火星轨道，赤道面法向量N在近焦点坐标系中为:N=[sinωsin i cosωsin i cos i]T，则T和R方向矢量可表示为:T= S×N，R=S×T，同理于2.1节有BT=B·T，BR= B·R，设下标NORM表示相应于标准轨道的值，则B平面的误差散布为

2.3 B平面参数偏导矩阵的求法

已经得到了B平面参数及B平面参数误差的表达式，但是仍然需要建立B平面参数与需要修正的速度增量之间的关系.凯兹纳发现目标星B平面参数偏差与轨道状态量偏差量之间存在很好的线性关系.下面给出这种线性关系的说明.

首先，定义参数TOF表示从修正点到达B平面的飞行时间，这样B参数实际上就由BT、BR和TOF构成.定义B平面参数对于速度改变量的偏导数.在火星赤道惯性坐标系下，记V沿X轴方向的速度改变量为△VX，那么定义 BT对 VX的偏导数如式(2)所示:

同理，BR、TOF对VX的偏导数以及BT、BR和TOF对VY和VZ的偏导数，由此得到B平面参数对V的偏导数矩阵Bp如式(3)所示:

考察偏导数矩阵Bp对△V的敏感度，将V沿三个坐标轴改变量的取值范围定为10-18km/s～101km/s，计算偏导数矩阵Bp中每个元素的值，以X轴方向为例，如图3所示.

图3 B平面参数对VX的偏导Fig.3 Partial derivative of B-plane parameters with respect to VX

从图3可以看出，当△V的X方向分量大致在10-12km/s～10-1km/s的量级范围内变化时，B参数对VX的偏导数基本为常数，Y、Z两轴类似，因此Bp是常数矩阵，所以当速度的改变量在上述范围内时，△B与△V有良好的线性关系，即有式(4):

速度修正量计算流程图如下所示:

图4 速度修正量计算流程图Fig.4 Flow chart of velocity correction algorithm

由于 B平面需要以火星赤道惯性系作为参考平面，因此在计算实际轨道 B平面参数时，需要将当前的位置矢量和速度矢量经过坐标系转换，由日心黄道坐标系转到火星赤道惯性系下.图5给出了各坐标系之间的几何关系:

(1)火星赤道坐标系O-NYZ，N是X轴指向，XY坐标面即火星赤道

(2)火星轨道坐标系O-N'YZ，N'是X轴指向，XY坐标面即火星轨道面

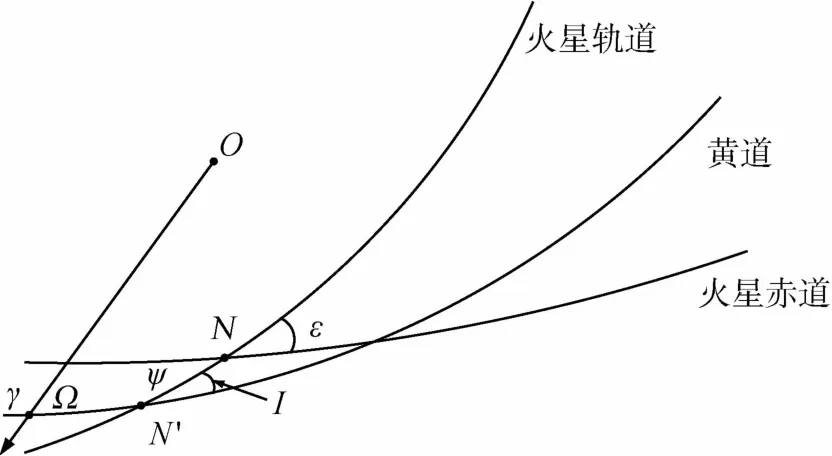
图5 火星中心坐标系示意图Fig.5 Sketch of Mars center coordinate system

(3)日心黄道坐标系O-γYZ，γ是X轴指向，XY坐标面即黄道面

上述坐标系中的O是火星的质量中心，N是火星轨道与火星赤道的交点，相当于地球的轨道(即黄道)与地球赤道的交点γ.N'是火星轨道与黄道的交点.γ是黄道与地球赤道的交点，即春分点.由此，探测器在日心黄道系到火星赤道系的坐标旋转矩阵为:RX(-ε)RZ(ψ)RX(I)RZ(Ω).4个旋转角的计算公式如式(4)和式(5)所示:

其中d的单位是地球日，JD(t)是t时刻对应的儒略日，JD(2000.0)是历元时刻对应的儒略日，其值为2451545.0，T即世纪数.

3 控制策略与仿真分析

控制策略需要回答的问题是何时修正，每一次修正多少.关于修正时机的选择，本文做简单的讨论，并给出一个易于工程实现的策略.火星探测的轨道飞行时间很长，对于一次修正后，其残差沿轨道传播仍有可能超出任务要求，所以一般要进行多次.修正过早可能由于定轨精度不够而使修正失去意义，修正过晚有可能因为误差传播过大而超出修正能力[1].20世纪60年代星际制导研究快速发展，如何确定最优修正次数和修正时刻以使修正燃料最少是研究的热点，Pfeiffer研究了动态规划方法[4]，Breakwell提出的间距比(Space Ratio)方法[5]，该方法的主要思想是尽快进行第一次修正，其后各次修正时间间隔与前一时间间隔之比为常数，直至满足误差要求，不再进行修正.美国勇气号(Spirit)和机遇号(Opportunity)火星探测器[6]的轨道修正策略中也充分重视了尽早修正这一原则.这里可以借鉴等间距比的思想，首先尽早修正.

本节结合本文涉及的火星探测器的实际情况，给出了三种修正方案，分别为修正一次，修正二次，修正三次，最终通过仿真说明了，修正三次的方案合理且能够实现轨道修正的目的，最终给出了在三次修正基础上余留一次机动修正和一次备份修正的控制策略.结合火星探测器轨控发动机性能、测轨精度、和姿控能力，估计中途修正速度大小执行误差± 0.5%，速度方向执行误差±0.1°，测轨精度上限为20～30km.目标轨道轨道倾角 95°，近火点高度300km.

3.1 修正一次方案分析

选择发射机会为2011年11月6日发射，考虑只修正一次的情况，表1给列出了在不同的修正时间进行修正需要的速度增量以及相关参数.

表1 不同时刻修正第一次的情况Tab.1 First correction at different times

表1中第一列对应的是探测器出地球影响球的修正时刻.从表1可以看出随着修正时刻的延后，所需要的速度修正量越来越大.通过仿真发现，用 B平面法试图在第32天后任选一个时刻进行修正时，算法无法收敛，这是由于计算出的|△V|的量级超过了10-1km/s，超出了偏导数矩阵Bp对△V的线性化范围.因此，需要尽早进行修正，本文将第一次修正的时间点放在探测器刚出地球影响球时.相对于探测器实际的速度而言，第一次修正的速度改变量是比较小的，后续轨道修正就是针对其残差的进行的，量级会更小.实际情况中，需要考虑执行误差、测轨误差等因素的影响，因此给出在考虑中途修正速度大小误差、速度方向误差和测轨误差的情况下，修正后最终到达火星时 B平面参数误差的分布情况图6所示.

图6 第一次修正后B平面参数误差分布Fig.6 B-plane parameters error distribution after first correction

由上述仿真实例可以分析得出:一次修正方案，在考虑了误差后，最终探测器到达火星时距离目标轨道偏移量较大，超出了误差要求，这是由于一次修正时，修正时刻较早，微小的误差在未来长时间的轨道运行中不断积累，导致最终无法到达预定目标.因此，一次修正方案无法满足任务要求，需要增加中途修正次数.

3.2 修正两次方案分析

根据控制策略，第一次修正时刻为探测器出地球影响球时，即距发射日期3.12天.第一次修正量:

△V=[7.30627 19.88104 -26.28166]T(m/s)，|△V|=33.75445(m/s)，考虑存在测轨误差、速度执行误差(包括方向和大小)，取随机误差下的某一次实际速度改变量:△V=[7.32264 19.83375 -26.29379]T(m/s)，选择不同的时刻进行第二次修正，求得速度修正量，仿真结果如表2所示.

由表2可以得出结论:第二次修正的速度量的量级小于第一次修正的速度量级，且第二次修正的速度量值随着时间间隔的增加而增加，但是增加的比较缓慢.如表2所示，第二次修正的速度修正量随时间的增幅很有限，因此，第二次修正时间点的选择限制可以放宽要求.本文设计在距第一次修正后的4个月进行第二次修正，计算的修正量如表2所示，同理于第一次修正，同时考虑测轨误差，速度执行误差，最终到达火星时B平面参数误差的分布情况的如图7所示.

表2 不同时刻第二次修正的情况Tab.2 Second correction at different times

图7 第二次修正后B平面参数误差分布图Fig.7 B-plane parameters error distribution after second correction

从图7中可以看出，第二次修正后，探测器最终到达火星时，B平面参数误差大幅度减小，但是在BT方向上仍有250km的误差，因此需要继续增加修正次数.

3.3 修正三次方案分析

当探测器接近火星时，其入轨精度需要尽可能的高.因此在修正两次方案的基础上，增加一次探测器进入火星影响球之前的修正，形成三次修正的方案.本文设计第三次修正距离第二次修正间隔175天，这样可以保证第三次修正点距离探测器到达火星影响球还有3～5天的时间余量.

第二次修正量:△V=[-3.49298 3.44780 0.71025]T(m/s)，取随机误差影响下的某一次实际速度改变量:△V=[-3.4773 3.42703 0.70552]T(m/s)，计算得到第三次修正需要的速度增量△V=[-0.01431 -0.12062 0.02096]T(m/s)，最终到达火星时B平面参数误差的分布情况的如图8所示.

图8 第三次修正后B平面参数误差分布图Fig.8 B-plane parameter error distribution after third correction

从图8中可以看出，经过三次修正，探测器到达火星影响球时，B平面参数误差可以达到25km.如果需要增加最终入射精度，即满足轨道倾角和近火点高度要求，可以增加一次机动修正.

以探测器到达火星影响球时进行一次机动修正为例，经过三次修正后，考虑误差影响，随机抽取探测器的一组状态值，r=[0.433077 5.336899 2.1767830]T×105km，υ=[-0.20324 -2.55276

-1.00312]T(km/s)，对应的轨道倾角为95.86°，近火点高度300.002km，可见由于考虑了实际的误差，导致探测器进入火星时不在预定轨道平面内，可以进行一次机动修正，计算得所需速度修正量为:

△V=[-0.5724 0.0271 0.0556]T(m/s)，修正后轨道倾角为95.00°，近火点高度为300.000km.在此基础上，可以再增加一次备份修正，目的是补救第三、四次修正可能存在的意外造成的修正失败.综上所述，控制策略如表3所示.

表3 控制策略Tab.1 Control strategy

4 结 论

1)当速度的变化量在10-12km/s～10-1km/s的量级范围内变化时，B平面参数对速度的偏导数矩阵是常数阵，可以直接建立B参数变化量与速度变化量之间线性关系.

2)给出了一个以三次修正为主，包含一次机动修正，一次备份修正的控制策略，通过仿真，验证了控制策略的可行性.

[1] 杨嘉墀.航天轨道动力学与控制(下)[M].北京:宇航出版社，1995 Yang JC.Spacecraft orbital dynamics and control(volume two)[M].Beijing:Aerospace Press，1995

[2] Kizner W.A method of describingmiss distances for lunar and interplanetary trajectories[R].Jet Propulsion Laboratory，1959，NASA-CR-63483;REPT.-674 65N85813

[3] Hintz C R，Chadwich C.A design technique for trajectory correction maneuvers[J].The Journal of the Astronautical Sciences，1985，33(4):429-443

[4] Pfeiffer C G.A dynam ic programming analysis ofmultiple of guidance correction of trajectory[J].AIAA Journal，1965，3(9):1674-1681

[5] Breakwell J V.Fuel requirements for crude interplanetary guidance[J].Advances in Astronautical Science，1960，(5):53-65

[6] Christopher L P，Behzad R，Julie A K.Mars exp loration rovers propulsivemaneuver design[C].AIAA/AAS Astrodynamics Specialist Conference and Exhibit，Providence，Rhode Island，16-19 August，2004

B-Plane M ethod-Based M idcourse Trajectory Correction M aneuver for M ars Probe

TANGWei
(Shanghai Institute of Spaceflight Control Technology，Shanghai 200233，China)

It is trajectory correction maneuver(TCM)that is absolutely important and has to be solved as the key problem during the Earth-to-Mars trajectory in the Mars exploration.Firstly，the B plane reference frame based on the target planet and target parameters are introduced.Then formulas of B plane parameters are deduced.In succession，it is validated that linear relationship exits between target parameters and the velocity correction value.Meanwhile the corresponding arithmetic flow chart is proposed.In the next place，taking the rational velocity maneuver error and the orbitmeasurement error into account，a control strategy containing threemain TCMs，one contingent TCM and one backup TCM is proposed and is proved possible and feasible by the simulation eventually.

Mars exploration;trajectory correction maneuver;B-plane

V423

A

1674-1579(2012)06-0050-06

唐 卫(1986—)，男，助理工程师，研究方向为航天器姿态、轨道控制.

2011-11-03

DO I:10.3969/j.issn.1674-1579.2012.06.011