高等代数在线性规划问题求解中的应用
2012-09-04范静
范 静
(上海第二工业大学理学院,上海 201209)
高等代数在线性规划问题求解中的应用
范 静
(上海第二工业大学理学院,上海 201209)
高等代数课程是数学类本科阶段最基本的核心课程之一,不仅是初等代数的延拓,也是后续课程——运筹学,尤其是线性规划部分的基础。运用高等代数知识求解了线性规划问题:利用线性规划问题标准型的线性约束条件是线性方程组的特点,从线性方程组的角度分析了可行解与最优解;利用线性规划问题标准型的矩阵形式,根据矩阵的知识推出基可行解与目标函数值的表达式,以及最优解的判别准则,并讨论了矩阵初等变换与单纯形法的联系。同时通过一个典型实例说明了以上各分析的正确性。
高等代数;线性规划;矩阵;线性方程组
0 引言
高等代数是用严密的逻辑推理方法来建立代数系统的理论体系,用公理化方法来统领不同的代数系统,用结构化方法来研究代数系统的内部结构的一门课程[1-2],其概念具有高度的抽象性,定理具有高度的概括性。它与其他科目的关联也十分紧密,文献[3-5]分别研究了高等代数与数学分析、概率论以及数学建模课程的内在联系。这里,本文研究高等代数与运筹学,特别是线性规划问题的密切联系。运筹学课程的主要任务是使学生理解优化决策的思想,在掌握基本理论的基础上,具备解决优化问题的能力。高等代数是运筹学的先修课程,虽然表面上两者是独立的知识体系,解题方法也有差异,但在很多方面两者却是相互渗透、彼此相通的。本文对高等代数方法在线性规划问题求解中的应用进行了探讨,希望能提高高等代数与运筹学的教学与研究水平。
线性规划的数学模型的标准形式[6]为

利用向量符号可表述为

利用矩阵符号可表达为

其中,

向量Pj对应的决策变量为。一般情况下,m 本文仅讨论线性规划问题可行域有界,即最优解存在的情况。由于线性规划问题的可行解是满足所有约束条件的解,且最优解必是可行解,因此,有必要从线性规划问题可行解入手,研究它的最优解。 根据高等代数的知识,(1)式或(2)式中的等式约束即为线性方程组。因而,满足非负条件的线性方程组的解均为线性规划问题的可行解。 1.1 线性规划问题的可行解 根据m=r( A)≤r( A, b)≤min{m, n+1}=m ,可得r( A, b)=r( A)=m 为了表示线性规划问题的可行解,需要先表示约束方程组的解。由(2)式得 将约束方程组的增广矩阵经过有限次的初等行变换,将Pj转化为ej(j=1,2,…,m),这里, 1.2 线性规划问题的最优解 众所周知,线性方程组若有无穷多解,其自由未知量的组合至多有种,按照如上方法可得到个基解。除去不满足非负条件的解,即得到基可行解。进一步地,线性规划问题的可行域实质上是由基可行解的连线构成的凸集。 根据运筹学知识,若线性规划问题存在最优解,则一定可以在某基可行解处得到。因而,只需比较所有基可行解的目标函数值即可得到最优解。 1.3 实例说明 由于含有2个决策变量的线性规划问题可以通过平面图形直观地观察其可行域,因此,本文选用以下线性规划问题进行具体说明。 对于线性规划问题(P) 其标准型记为(SP) 表1 6组不同的基解Tab. 1 Six different basic solutions 由图1可得,基可行解对应点O,A,B及C连线形成的四边形区域即为可行域。这也将高等代数问题中线性方程组的无穷多解进行了图形化表示。进而,比较四个点O,A,B及C的目标函数值,即得B点对应的解为最优解,最优值为46/3。 图1 问题(P)的可行域及基解Fig. 1 The feasible region and the fundamental solutions of problem (P) 根据高等代数中分块矩阵的知识,由线性规划问题的矩阵表达式(3)可直接得到基可行解及目标函数值的计算表达式。 2.1 线性规划问题的基可行解及目标函数值 将约束方程组的系数矩阵A中除B之外的子矩阵记为N,则A=(B, N),且N是非基变量的系数矩阵。将变量矩阵X相应地划分为 (XB, XN)T,同时将目标函数的系数C划分为(CB,CN),分别对应基变量与非基变量。此时,线性规划问题的矩阵形式(3)可进一步地表示为 将其中的等式约束移项后,得到BXB=b−NXN。由于B非奇异,可将等式两边左乘B−1,故得到基可行解的表达式(6): 带入(5)式中的目标函数,得到目标函数值的计算表达式(7): 若非基变量X=O,可得到一个可行解X = (XB, XN)T= (B−1b, O)T,这时目标函数z=C B−1b。若C−C B−1N N B NB的某些分量大于零,则可通过增加XN相应分量的取值而得到更大的目标函数值。因此,若取恰当的基矩阵B,使得CN−CBB−1N的所有分量均小于等于零,则对应可行解为最优解。这个结论与运筹学的最优解的判别准则不谋而合。在运筹学中,CN−CBB−1N的各分量称为对应非基变量的检验数。当检验数存在正数时,可行解不是最优解,目标函数值还可以增加; 而当所有检验数均小于等于零时,可行解必为最优解,目标函数值为最优值。 2.2 实例说明 2.3 矩阵运算与单纯形法的联系 实际上,2.2中所有计算都可以通过矩阵的初等行变换求得。将目标函数行(也即检验数行)放置在增广矩阵的下一行,进行初等行变换,使基矩阵B(见实线框)变换为E,并使目标函数行的对应部分(见虚线框)变换为O。可得目标函数行右端常数的相反数即为最优目标函数值。 根据高等代数的知识,矩阵的初等行变换相当于矩阵左乘一个初等矩阵。于是,将矩阵的初等行变换利用表格的形式来呈现,即为单纯形表。初始单纯形表(见表2)为 表2 初始单纯形表Tab. 2 Initial simplex tableau 用B−1左乘表2的第二行,用左乘表2的第三行,可得到新的单纯形表(见表3)。 表3 新单纯形表Tab. 3 New simplex tableau 若此表的解不是最优解,可重新选基矩阵以得到改进解,直至得到最优解。但从形式上来看,不论是改进单纯形表还是最优解对应的最优表,它们的形式与表3完全相同。因此,单纯形法的计算实质上就是矩阵的初等行变换。 本文从高等代数的角度研究了可行域有界的线性规划问题的可行解及最优解,并通过实例进行了具体分析说明。本文分别从线性方程组以及矩阵两个方面进行了研究。一方面,利用线性方程组的知识表示了可行解以及基解,进而比较所有基可行解的目标函数值以得到最优解与最优值;另一方面,利用矩阵的知识得到基可行解与目标函数值的计算表达式,并分析了运筹学中最优准则的合理性,进一步地讨论了矩阵初等行变换与单纯形法的关系。前者的优势在于可行解的表示,而后者的优势在于最优解的分析与判别。将两者相结合,则可达到对线性规划问题的更深层的理解。 [1] 刘娟, 马宝林. 浅谈高等代数的“纵观”与“横联”[J]. 长沙大学学报, 2010, 24(5): 97-98. [2] 王萼芳, 石生明. 高等代数[M]. 北京: 高等教育出版社, 2003. [3] 凌征球, 龚国勇, 龚文振. 高等代数在数学分析解题中的某些应用[J]. 玉林师范学院学报, 2010, 31(5): 34-37. [4] 翟富菊, 吴海燕. 概率论与高等代数的相互渗透[J]. 中国科教创新导刊, 2010(1): 94-94. [5] 程国, 刘亚亚, 赵鹏军. 基于数学建模思想的高等代数课程教学研究[J]. 商洛学院学报, 2011, 25(6): 15-18. [6] 《运筹学》教材编委会. 运筹学[M]. 北京: 清华大学出版社, 2005. The Applications of Advanced Algebra in Linear Programming FAN Jing Advanced Algebra is one of the basic core courses for all undergraduates in the department of mathematics. It is not only the extension of elementary mathematics, but also the foundation of Operations Research, especially of the Linear Programming. The knowledge of advanced algebra is used to solve the linear programming problem. Because the linear constraints of the standard format of the linear programming problem are the linear equations, the feasible solutions and the optimal solution are deduced from the point of view of the linear equations. According to the matrix form of the standard format of the linear programming problem, the expressions of the basic feasible solutions and the corresponding objective function value can be obtained, in addition to the criteria for the optimal solution. Moreover, the close relationship between the elementary transformation of the matrix and the simplex method is analyzed by the knowledge of the matrix. The correction of the above analysis can be illustrated by one typical example. advanced algebra; linear programming; matrix; linear equations O15 A 1001-4543(2012)03-0214-05 2012-07-07; 2012-08-03 范静(1979-),女,山西长治人,讲师,在读博士,主要研究方向为运筹学,电子邮箱fanjing@sf.sspu.cn。 上海第二工业大学重点课程建设项目(No. A20KC110002)1 利用线性方程组的知识求解线性规划问题




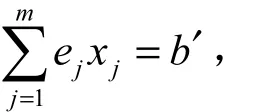




2 利用矩阵的知识求解线性规划问题







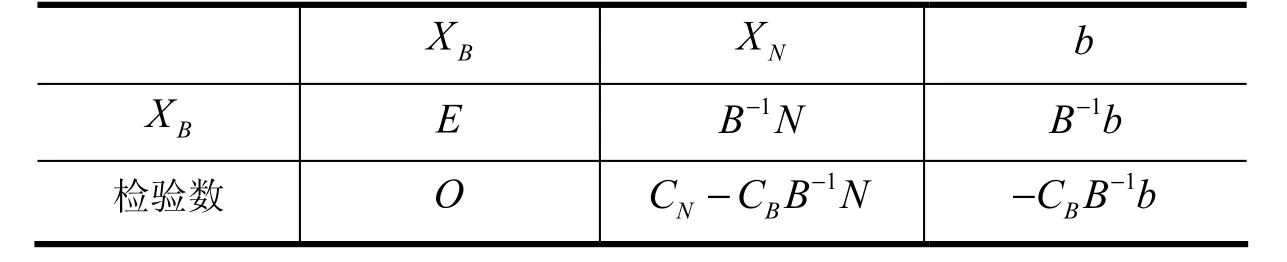
3 总结
( School of Science, Shanghai Second Polytechnic University, Shanghai 201209, P. R. China )
