目标高度对广域多点定位系统精度的影响

何东林,吴宏刚,王 洪,徐自励

(1.中国民用航空局第二研究所网络工程学院,成都 610041;2.电子科技大学电子工程学院,成都6 11731)

1 引 言

广域多点定位(Wide Area Multilateration,W AM)技术是针对空中航路和终端区域的一种新型监视技术。该技术通过多站接收民航飞机的A/C模式和S模式应答信号,采用到达时间差(Time Difference of Arrival,TDOA)算法,确定空中飞机的位置。现有二次监视雷达(Secondary Surveillance Radar,SSR)覆盖不全,有盲区,且成本高,因此在欧美一些山区航路和终端区已安装了W AM 系统用于飞机监视[1]。

WAM系统由多个分布式的地面接收站构成,系统的精度受到各接收站安置几何分布的影响,即几何精度稀释(Geometrical Dilution of Precision,GDOP)问题[2-3]。文献[4-7]对时差定位的系统定位精度进行了分析,文献[4]和文献[5]侧重对站点几何位置对定位精度的影响分析,文献[6]主要对二维定位解中目标高度引起的误差进行分析,文献[7]主要分析了站址测量误差对系统二维定位精度的影响,文献[8]研究了多点定位站点优选和故障定位方法,文献[9]主要对如何提高系统定位效率进行了研究。但是上述文献都没有针对目标高度不同对WAM定位精度的影响进行分析。

本文考虑实际广域站点布局的各种情况,对相同高度层和不同目标高度层的系统定位精度进行了分析,得出了水平精度稀释(Horizontal Dilutionof Precision,HDOP)和垂直精度稀释(Vertical Dilution of Precision,VDOP)随高度的变化规律,最后对同高度层不同站点布局和基线长度对定位精度的影响进行了分析,并由此解决了航路不同高度层条件下WAM系统站点的设计和定位精度保障问题。

2 WAM系统定位精度分析算法

多点定位是一种双曲线/面定位技术,根据目标到各站点与参考站点的达到时间差计算目标位置,定位精度与TDOA误差和站点布局有关,三者的关系为

式中,σs为广域多点定位系统位置精度,σTDOA为TDOA测距精度,G表示GDOP。GDOP决定了站点布局的设计,并直接影响系统定位精度,因此如何减小GDOP值对控制系统精度非常重要。

首先对到达时间差测量方程组进行描述。假设x=[rxryrz]T为飞机目标的空间位置矢量,xi=[rxiryirzi]T为第 i个广域多点定位地面接收站的位置矢量,共有N个接收站。对于N个接收站,到达时间测量方程组写成矩阵形式为

式中,c为信号传播速度,Tm为信号到达接收站时间的测量值,T0为目标发射信号的时间,r为目标到接收站的距离,n为测量噪声。假设测量噪声均值为零,彼此独立,则其协方差矩阵为

广域多点定位系统采用到达时间差(TDOA)算法进行双曲线定位,在式(2)中为了消去共同参量T0,用时间差列出时差测量方程组:

式中,i取值为2～N。这里只有(N-1)个时差公式。

用矢量矩阵来表示测量噪声的差值,有

式中,差分矩阵

则到达时间差的协方差矩阵为

通过最小二乘法线性估值法,得到时间差测量定位协方差矩阵为

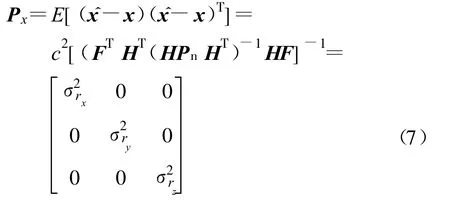
式中 ,σrx、σry、σrz分别是 x、y 、z 方向上的定位误差标准差,参考点x0到接收站的单位矢量为

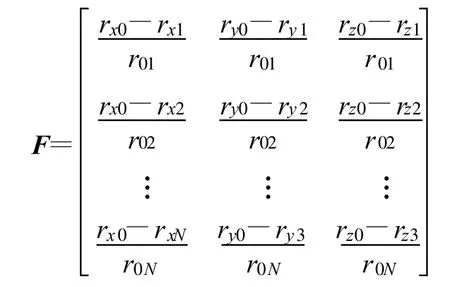
由式(7)和GDOP定义有:

水平位置精度误差用HDOP来描述:

系统高度精度误差通过VDOP来描述:

这里,H表示HDOP,V表示VDOP,对于广域航路和终端区来说,HDOP控制水平定位精度,VDOP控制垂直定位精度,HDOP和VDOP值越大,表示定位精度越低。下面针对空中飞机,进行HDOP和VDOP的仿真分析。

3 仿真与分析

3.1 同高度层HDOP和VDOP分析

由GDOP算法公式推导可知,GDOP取决于广域多点定位系统各个接收站的布局和目标位置等。下面对空中航路飞机进行了HDOP、VDOP算法分析,经过算法仿真,得到了不同条件下的仿真结果。广域多点定位系统4接收站即可进行三维位置解算定位,但在实际运行中考虑系统冗余性和可靠性,一般进行5站同时覆盖定位。这里我们首先对标准5站布局进行仿真分析。

仿真条件:监视区域选取50 km×50 km区域,标准5站布局,中间站点坐标为(0,0),周边4站距中间站点的基线距离都为20 km,测量误差设置为10 ns,目标高度分别为3 km和8 km。图1、图2分别是目标高度3 km和目标高度8 km时5站HDOP结果,图3、图4分别是目标高度3 km和目标高度8 km时5站VDOP结果。

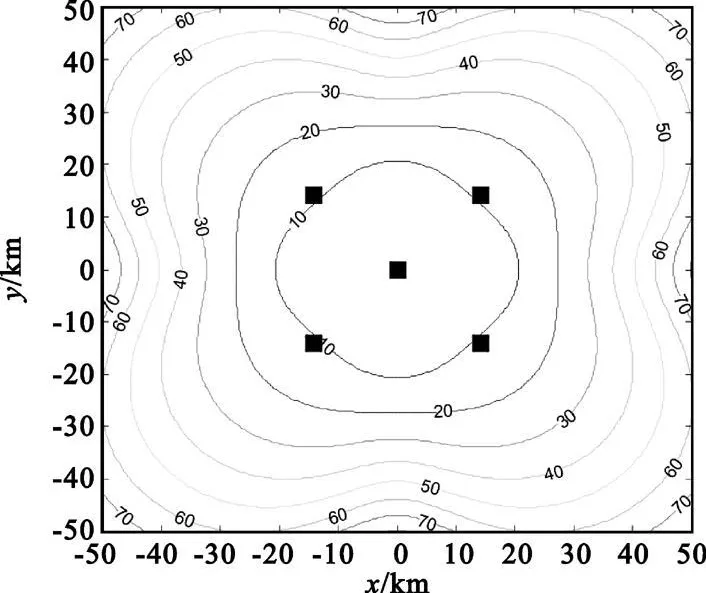
图1 对称5站HDOP(高度3 km)Fig.1 HDOP of 5 symmetric stations(3 km height)

图2 对称5站HDOP(高度8 km)Fig.2HDOP of 5 symmetric stations(8 km height)

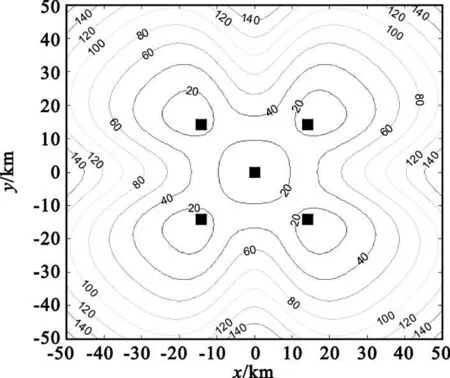
图3 对称5站VDOP(高度3 km)Fig.3 VDOP of 5 symmetric stations(3 km height)

图4 对称5站VDOP(高度8 km)Fig.4 VDOP of 5 symmetric stations(8 km height)

经分析可以得出,同目标高度层当高度较低时,HDOP值典型小于VDOP。当目标高度较高时,在接收站点所围区域内HDOP小于VDOP,说明广域多点定位系统定位精度在站点所围区域内受垂直定位精度影响较大。在接收站点所围区域外两站开口方向,HDOP小于VDOP;在站点连线延长线上,HDOP大于VDOP。

从图1和图2还可以看出,布局固定时不同目标高度层水平定位精度变化不大,但垂直定位精度变化较大。下面将针对上述结果对不同目标高度层时的HDOP和VDOP进行仿真分析。

3.2 高度层变化时HDOP和VDOP结果分析

结合上述同高度层仿真结果,保持仿真条件不变,取标准5站布局站点所围区域内点(10,0),所围区域外两站开口延长线点(30,0),以及站点连线延长线点(30,30),作为典型目标位置点进行HDOP和VDOP分析。

图5的HDOP结果表示了目标高度层变化时系统水平定位精度变化情况,图6的VDOP结果表示了目标高度层变化时系统垂直定位精度变化情况。可以看出,目标高度变化时水平定位精度变化不大,但垂直定位精度变化较大。在目标高度较低时,垂直定位精度随着目标高度降低显著变差,且明显差于水平定位精度。目标高度较高时垂直定位精度变化不大,在站点所围区域内、两站开口延长线点VDOP值大于HDOP,在站点连线延长线上点VDOP稍小于HDOP。

考虑系统定位精度由水平和垂直定位精度两部分组成,因此目标高度变化对广域多点定位系统定位精度影响较大。

图5 对称5站HDOP随目标高度变化结果Fig.5 HDOP of 5 symmetric stations changedwith target height

图6 对称5站VDOP随目标高度变化结果Fig.6 VDOP of 5 symmetric stations changed with target height

3.3 不同站点布局、同高度层时VDOP结果分析

从前面分析中可以看出,广域多点定位系统中目标高度变化时对系统垂直定位精度影响较大,因此下面我们进一步分析在目标高度一定的情况下,改变站点布局和基线长度对系统垂直定位精度的影响。

以两种典型的4站定位布局为例进行分析。首先设置站点布局为4站对称和4站星形布局,仿真监视区域仍选取50 km×50 km区域,站点间基线长度均为20 km,测量误差设置为10 ns,目标高度设为8 km,其VDOP结果见图7和图8。

图7 对称4站VDOP仿真结果(高度8 km,基线20 km)Fig.7 VDOP of 4 symmetric stations(8 km height,baseline 20 km)

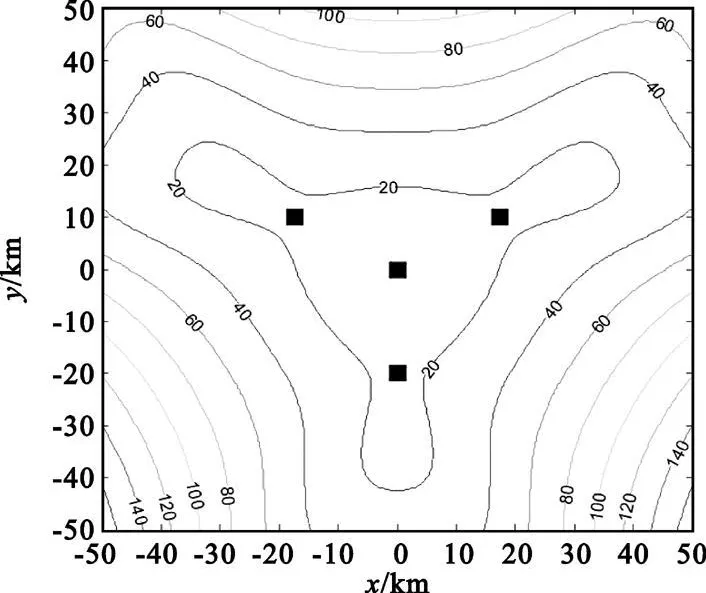
图8 星形4站VDOP仿真结果(高度8 km,基线20 km)Fig.8VDOP of 4 star stations(8 km height,baseline 20 km)

从图7中可以看出,4站对称布局方式,在每两站开口中心线方向无法有效定位,VDOP存在明显“十”字发散现象,该种布局方式实际中不适合采用。而从图8中看出,4站星形则是一种比较好的布站方式,垂直定位精度有保障,但其缺点是系统冗余度不够,可靠性较低。因此,在目标高度层不变时,不同站点布局形式可以提高广域多点定位系统垂直定位精度。

下面我们再对保持高度层不变,调整基线长度对系统定位精度的影响进行分析。图9是在上述星形布站方式仿真条件基础上,仅调整基线长度为30 km。可以看出增加基线长度一定程度上提高了广域多点定位系统的垂直定位精度。

图9 星形4站VDOP仿真结果(高度8 km,基线30 km)Fig.9 VDOP of 4 star stations(8 km height,baseline 30 km)

在实际外场测试中,为了保证包围中心区域的精度,采用了类似星形的布站架构,基线选取为20 km左右,实测定位效果较好。

上述仿真分析均考虑了外场应用情况,仿真基线设置和高度层变化符合实际环境,在实际外场测试中,也验证了该分析方法的有效性。

4 结 论

目标高度对广域多点定位系统定位影响较大,特别是垂直定位精度在高度较低时降低明显。在高度不变的情况下,适合的布站形状和基线长度可提高系统定位精度。本文通过针对广域多点定位系统的不同布局方式,调整目标飞行高度,分析了水平精度稀释和垂直精度稀释的变化规律,结果准确可靠,对实际布局中如何保障系统定位精度具有重要参考价值。

[1] 吕小平.MDS技术在我国民用航空的应用探讨[J].空中交通管理,2006,23(9):4-11.LV Xiao-ping.Discussions on the Application of MDS Technology in China Civil Aviation[J].Air Traffic Management,2006,23(9):4-11.(in Chinese)

[2] Yarlagadda R,Ali I,Al-Dhahir N,et al.GPS GDOP metric[J].IEE Radar,Sonar Navigation,2000,147(5):259-264.

[3] 王洪,刘昌忠,汪学刚,等.一种多点定位的目标位置精确解算方法[J].航空学报,2011,32(7):1269-1274.WANG Hong,LIU Chang-zhong,WANG Xue-gang,et al.A target position exact solution method of multilateration[J].Acta Aeronautica et Astronautica Sinica,2011,32(7):1269-1274.(in Chinese)

[4] Sharp I,Kegen Y.GDOP Analysis for Positioning System Design[J].IEEE Transactions on Vehicular Technology,2009,58(7):3371-3382.

[5] 易云清,徐汉林,沈阳.时差定位模型与定位精度分析[J].电子信息对抗技术,2010,25(3):16-20.YI Yun-qing,XU Han-lin,SHEN Yang.Analysis of TDOA Location Model and Location Precision[J].Electronic Information Warface Technology,2010,25(3):16-20.(in Chinese)

[6] 冯富强,杨黎都,陈永光.目标高度对三站时差定位精度的影响[J].电子对抗技术,2005,20(2):14-16.FENG Fu-qiang,YANG Li-du,CHEN Yong-guang.The Influence of Target Altitude on Accuracy of Tri-Station TDOA Location System[J].Electronic Warfare Technology,2005,20(2):14-16.(in Chinese)

[7] 赵琨,何青益.基于GDOP的三站时差定位精度分析[J].无线电工程,2012,42(5):15-17.ZHAO Kun,HE Qing-yi.Analysis of Location Precision in Tri-station TDOA Location System with GDOP[J].Radio Engineering of China,2012,42(5):15-17.(in Chinese)

[8] 吴宏刚,刘昌忠,黄忠涛.机场场面多点定位系统远端站优选方法[J].电讯技术,2009,49(12):5-8.WU Hong-gang,LIU Chang-zhong,HUANG Zhong-tao.Multilateration Sation Selection Method for Airport Surface Surveillance[J].Telecommunication Engineering,2009,49(12):5-8.(in Chinese)

[9] 刘军,解嘉宇,郭继周.多基地雷达马氏定位算法优化[J].电讯技术,2010,50(7):97-100.LIU Jun,XIE Jia-yu,GUO Ji-zhou.Optimization of Markov Estimation Algorithm for Multistatic Radar Positioning[J].Telecommunication Engineering,2010,50(7):97-100.(in Chinese)