一种多指标综合评价和决策的新方法

2012-09-03王积建

统计与决策 2012年24期

关键词：权重理想距离

王积建

（浙江工贸职业技术学院，浙江温州 325027）

一种多指标综合评价和决策的新方法

王积建

（浙江工贸职业技术学院，浙江温州 325027）

在多指标综合评价和决策问题中，文章通过引入负理想距离这一因素，解决了当两个方案在相似系数和正理想距离都相等时不能评判的问题.所建立的综合评价函数既兼顾了相似系数、负理想距离和正理想距离这三个因素，又进行了无量纲化处理而具备了直接可加性，使得评价结果更全面、更科学、更合理、更可靠。

综合评价；相似系数；理想解

0 引言

多指标综合评价是实践中经常采用的一种决策方法，任何一种综合评价模型都可以表示为Z=f(R,W)的形式，于是关于综合评价方法的研究大致可以归结为4个方向：

（1）数据标准化方法的研究，即R的确定方法，以及数据标准化方法对评价结果的影响研究[1]；

（2）权重的确定方法研究，即W的确定方法有主观权重、客观权重和组合权重；

（3）综合评价函数的选取,即 f的确定方法.有线性加权法，模糊优选法[2]等；

（4）多方法评价结论的非一致性研究[3～6]，以及由此引出的组合评价法[7～13]。

本文从改进综合评价函数 f的角度进行探讨。

文献[14]提出了多指标评价的TOPSIS方法，即

其中，di+表示方案Ai到正理想方案A+的距离，di-表示方案Ai到负理想方案A-的距离，fi越大表示方案Ai越优.这种评价函数有明显的缺陷。

文献[15]提出多指标评价函数为：

其中，Di表示方案Ai到正理想方案A+的投影，fi越大表示方案Ai越优。文献[16]指出，这种评价函数也有明显的缺陷，如图2所示，由于D1=D2，所以无法判定A1与A2的优劣，建议将多指标评价函数改进为

fi越大表示方案Ai越优。文献[17]指出，这种评价函数也有明显的缺陷，即在图3的情况下，由 D1＞D2,d1+=d2+而评判A1优于A2是错误的，建议将多指标评价函数改进为：

其中，ri表示方案Ai与正理想方案A+的相似系数（即向量Ai和A+的夹角余弦值），fi越大表示方案Ai越优。

笔者认为，（4）式同样有缺陷。首先，当 r1=r2,d1+=d2+时，将无法判定A1与A2的优劣；其次，由于ri测度的是方案Ai与正理想方案A+在方向上的差异性，而di测度的是方案Ai与正理想方案A+在距离上的差异性。由于方向和距离是相互独立的，所以ri和di在数量上缺乏可比性，因而不具备直接可加性。

基于以上分析，笔者认为，首先，应该将方向测度和距离测度进行无量纲化处理，即将ri和di分别进行无量纲化处理，然后再相加；其次，为了解决在r1=r2,d1+=d2+时无法评判的问题，需要引入负理想方案A-，并设di-表示方案Ai到负理想方案A-的距离，di-越大表示方案Ai越优。由于d1-＞d2-，所以应该判定A1优于A2，于是我们建议将多指标评价函数改进为：

1 基本原理

问题描述：设有m个方案A1,A2,...,Am，每个方案有n个指标C1,C2,...,Cn；xij为方案Ai在指标Cj下的值；i=1,2,...,m; j=1,2,...,n；xij＞0。于是初始化决策矩阵为X=(xij)m×n。现对m个方案A1,A2,...,Am进行综合评价并排序。

第1步，将X=(xij)m×n矩阵进行一致化、无量纲化处理，得标准化矩阵：

区间型指标的标准化公式为

所有指标值 xij经过标准化后转化为效益型，且rij∈[0 , 1]内。

第2步，确定权向量w=(w1,w2,...,wn)。权重分为主观权重、客观权重、主客观组合权重，主观权重有专家打分法、层次分析法等；客观权重有标准差法、离差最大化法等。

第3步，确定正理想方案A+和负理想方案A-。令

第9步，根据贴近度的大小对所有方案的优劣进行排序，贴近度越大方案越优。

定义1称方案Ai到正理想方案A+的距离为方案Ai的正理想距离；称方案Ai到负理想方案A-的距离为方案Ai的负理想距离。

定义2称方案Ai与正理想方案A+的向量夹角余弦值为方案Ai的相似系数。

2 实例

我们取2009年全国31个省、市、自治区规模以上工业企业主要经济效益指标数据，对这些省、市、自治区的规模以上工业企业主要经济效益进行综合评价并排序。原始数据如表1所示[18]。

C1——总资产贡献率（单位：%）；

C2——资产负债率（单位：%）；

C3——流动资产周转次数（单位：次/年）；

C4——工业成本费用利用率（单位：%）；

本研究通过观察右胸导联(V3R、V4R、V5R)心电图，发现V3R、V4R、V5R导联的R波振幅比率在两组之间比较，差异均有统计学意义，且根据V3R导联R波振幅比率的心电图算法，其ROC曲线下面积较大；以V3R导联R波振幅比率≥0.41鉴别LVOT起源的敏感性为81.4%，特异性为83.3%。研究证实，右胸导联心电图对室早左右室起源的鉴别具有一定的临床价值，且V3R导联R波振幅比率的诊断价值较高。

C5——产品销售率（单位：%）；

其中，C2为成本型指标，其余都是效益型指标。

使用公式（7）、（8）对表1数据标准化，得标准化数据如表2所示。

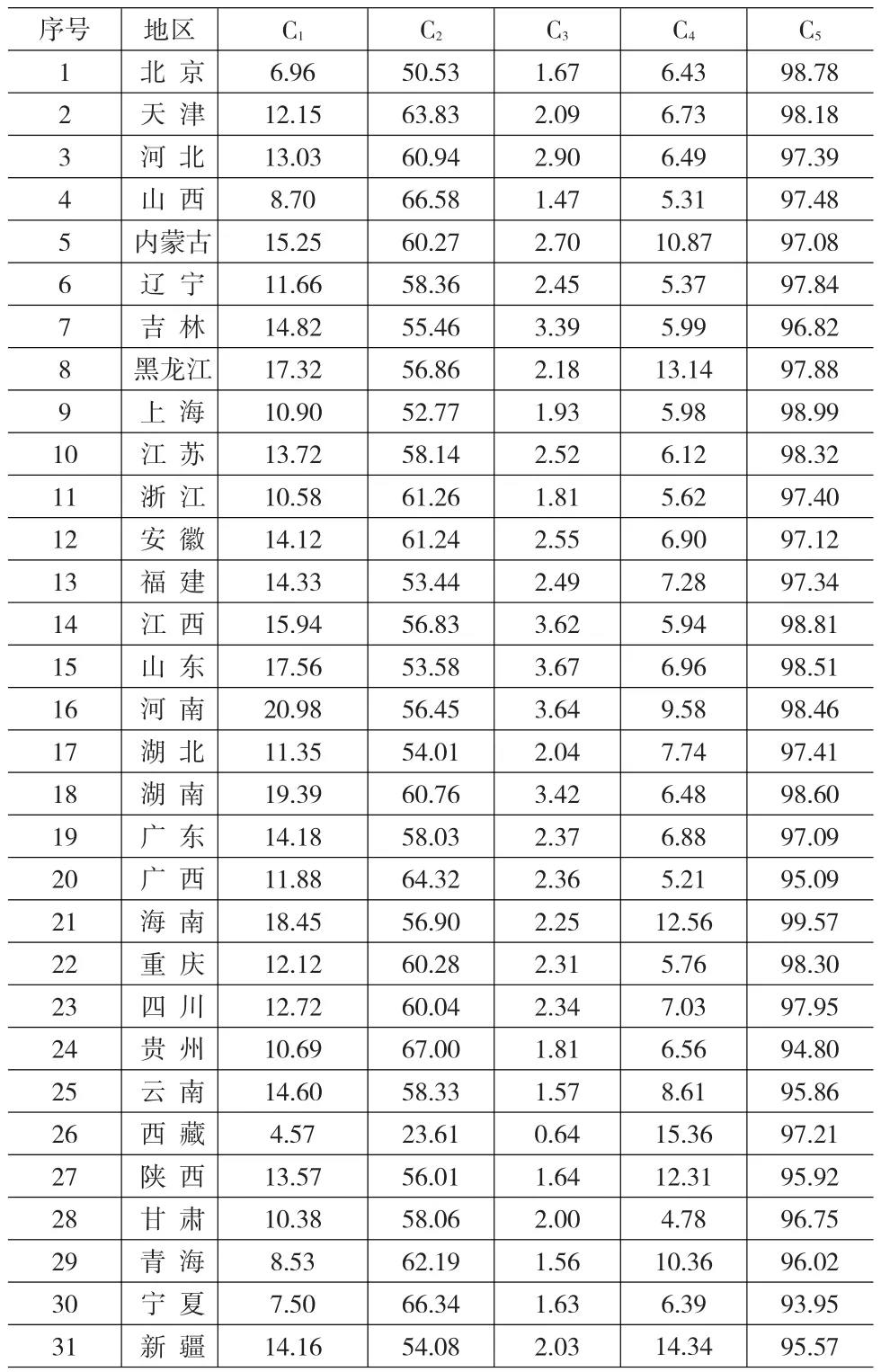
表1 2009年我国31个省市区规模以上工业企业主要经济效益指标

取偏好系数α=0.5，计算结果和排序结果如表3所示。

为了将本文结果与文献[17]结果进行比较，将文献[17]的计算结果也放在表3的第8、9、10、11列.下面进行比较分析：

（1）在文献[17]方法中，相似系数的总和是27.1534，正理想距离的总和是8.567，相似系数总和是正理想距离总和的3倍多，因此相似系数和正理想距离这两个变量具有显著的不可忽略的数量级差异，如果把它们直接相加作为公式（4）的分母，就会出现“大数吃小数”的现象，相当于夸大了相似系数的作用而削弱了正理想距离的作用，评价结果就会倾向于方向的一致性而忽视距离的一致性，评价结果必然出现偏差。

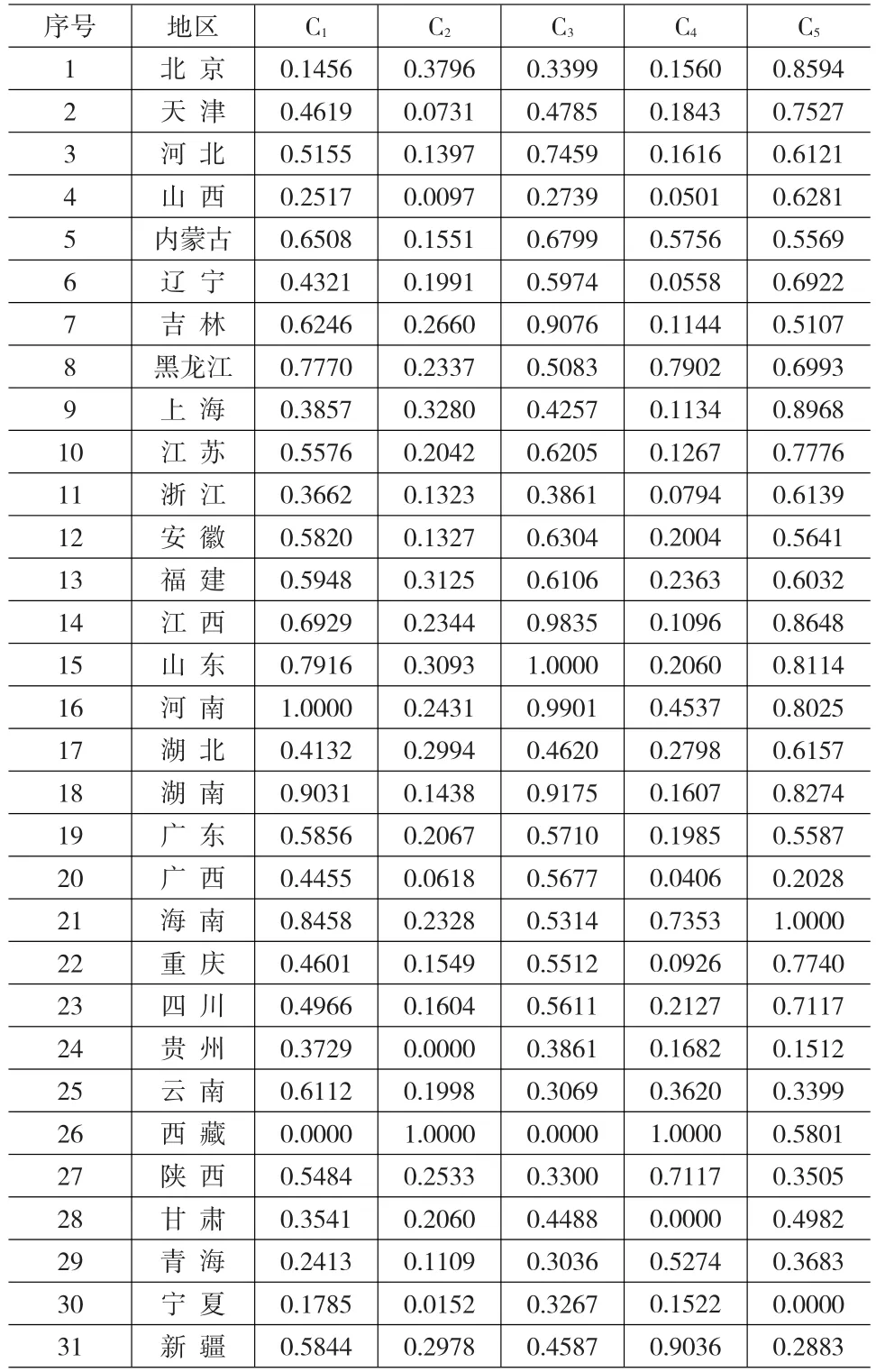
表2 2009年我国31个省市区规模以上工业企业主要经济效益指标的标准化值

（2）两种评价方法的排序结果在6个省市区上是一致的，分别是第1、4、20、23、25、31名，这说明两种方法在最优方案和最劣方案的评价上是一致的。

（3）两种评价方法的排序结果在其余的25个省市区上有差异，有些差异还很大，说明两种方法具有显著的差异，不可互相代替。

（4）差异最大的是西藏，其次是吉林、湖北、广东和云南.以西藏来说，在本文方法中，西藏排名于云南之前，而在文献[17]的方法中却相反.西藏在指标C2、C4、C5上的标准化指标值分别大于云南，而且这三个指标的权重之和为0.5984，大于其余指标的权重之和，所以西藏排名于云南之前是合理的。

在本文方法中，吉林排名于广东之前，而在文献[17]的方法中却相反.吉林在指标C1、C2、C3上的标准化指标值分别大于广东，而且这三个指标的权重之和为0.5540，大于其余指标的权重之和，所以吉林排名于广东之前是合理的。

在本文方法中，湖北排名于湖南之后，而在文献[17]的方法中却相反.湖北在指标C1、C3、C5上的标准化指标值分别小于湖南，而且这三个指标的权重之和为0.6074，大于其余指标的权重之和，所以湖北排名于湖南之后是合理的。

表3 2009年我国31个省市区规模以上工业企业主要经济效益指标综合评价及排序

3 结束语

本文在多指标综合评价和决策问题中，在评价函数中引入了负理想距离这一因素，解决了当两个方案在相似系数和正理想距离都相等时不能评判的问题，所建立的综合评价函数兼顾了相似系数、负理想距离和正理想距离这三个因素，使得评价结果更全面、更可靠；同时，将相似系数、负理想距离和正理想距离进行了无量纲化处理，使得评价函数更合理、更科学。

[1]周惠成,朱永英.优劣方案及规格化公式选取对模糊优选模型评价结果影响研究[J].大连理工大学学报,2008,48(1).

[2]杨志辉,陈铁牛,刘龙章.基于改进层次分析法的模糊优选模型[J].数学的实践与认识，2010，40（10）.

[3]陈衍泰,陈国宏,李美娟.综合评价方法分类及研究进展[J].管理科学学报,2004，（4）.

[4]李光，吴祈宗.基于粒度的多方法评价结论一致性研究[J].数学的认识与实践，2010,40（7）.

[5]Thomas Ray.Evangelos Triantaphyl⁃lou.Procedures For the Evaluation of Conflicts in Rankings of Alternatives[J].Computers&Industrial Engineer⁃ing，1999,36.

[6]Stefan Hajkowicz,Andrew Higgins.A Comparison of Multiple Criteria Analysis Techniques for Water Re⁃source Management[J].European Journal of Operational Research，2008,184.

[7]陈国宏,李美娟,陈衍泰.组合评价及其计算机集成系统研究[M].北京：清华大学出版社，2007.

[8]王彭德,熊明.医院管理综合评价方法的组合与优化[J].数学的认识与实践,2010,40（7）.

[9]郭显光.一种新的综合评价方法——组合评价法[J].统计研究，1995，（6）.

[10]曾宪报.关于组合评价法的事前事后检验[J].统计研究,1997，（6）.

[11]毛定祥.一种最小二乘意义下主客观评价一致的组合评价方法[J].中国管理科学,2000,8（5）.

[12]陈国宏.组合评价系统综合研究[J].复旦学报（自然科学版），2003，（5）.

[13]马溪骏.基于兼容一致性方法集成组合评价研究[J].中国管理科学,2006，（4）.

[14]岳超源.决策理论与方法[M].北京：科学出版社，2003.

[15]王应明.一种多指标决策与评价的方法——投影法[J].统计研究，1998，（4）.

[16]邱根胜.一种多指标决策与评价的新方法[J].数学的认识与实践，2004,34（11）.

[17]张慧颖.另一种新的多指标综合评判方法[J].数学的认识与实践，2010,40（7）.

[18]中华人民共和国国家统计局.中国统计年鉴2010[ED/OL].http://www.stats.gov.cn/tjsj/ndsj/2010/indexch.htm,2011/11/19.