参数假设检验中的若干基本问题研究

杨桂元，刘德志

（安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030）

参数假设检验中的若干基本问题研究

杨桂元，刘德志

（安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030）

文章对参数统计检验中的基本原理、势函数与两类错误、检验的 p值和单边检验的假设与拒绝域等若干基本问题进行了研究，并分析了它们之间的关系，阐明了参数的区间估计和假设检验的关系，揭示了参数统计推断的本质。

参数统计检验；两类错误；势函数；p值；拒绝域

0 引言

随着科学技术和生产的不断发展,数理统计的应用更加广泛。而统计假设检验问题在统计推断中占有很重要的地位。人们常常假设总体为正态分布,在正态总体下衍生出了统计学的三大分布——t分布、F分布和χ2分布,产生了与此相关的抽样分布，并且研究了正态总体期望和方差的各种统计推断问题。区间估计和假设检验是统计推断中的重要内容，是两个不同的统计概念，但它们又有着密切的联系，在某种意义下是同一问题的两个方面。这两种统计推断方法都是通过对具体问题的随机抽样所得到的样本观察值，用数理统计学的方法进行统计分析并做出判断。深刻理解参数假设检验中的若干基本问题，了解统计推断中参数的假设检验与区间估计之间的关系、不同类型的假设检验适用范围及应注意的问题，对正确的掌握和应用统计推断方法是极为重要的。然而这部分内容不易理解，从而初学者和实际应用的工作者在解决具体问题时会遇到一些困难。本文将就此问题展开讨论。

1 假设检验的定义与基本原理

在假设检验中，常把一个被检验的假设称为原假设或者零假设，用H0表示。通常将不应轻易加以否定的假设作为原假设，当H0被拒绝时而接受的假设称为备择假设，用H1表示，它们常常成对出现。

由样本(x1,x2,…,xn)对假设进行推断总是通过一个恰当的统计量T(x1,x2,…,xn)完成的，该统计量T(x1,x2,…,xn)称为检验统计量。使原假设被拒绝的样本观测值所在区域称为拒绝域，一般它是样本空间Ω的子集，并用W表示，Wˉ称为接受域；统计量T(x1,x2,…,xn)的拒绝域记为T(W)。

假设检验的基本原理是小概率事件原理，即：概率很小的事件在一次试验中实际上是不可能发生的；基本方法是“反证法”，若小概率事件发生则拒绝原假设H0从而接受备择假设H1，否则接受原假设H0。

2 假设检验的两类错误

对于给出的拒绝域W，由于抽样的随机性，我们做出的判断不可能绝对正确，它可能会犯两类错误。

第一类错误：当H0为真时，但(x1,x2,…,xn)∈W ，从而拒绝H0。这种错误称为第一类错误，又称为“弃真错误”，其发生的概率通常记为α，即

就是假设检验的显著性水平。

第二类错误：在H0不真时，但(x1,x2,…,xn)∈Wˉ，从而接受H0。这种错误称为第二类错误，又称为“纳伪错误”或你“取伪错误”，其发生的概率通常记为β，即

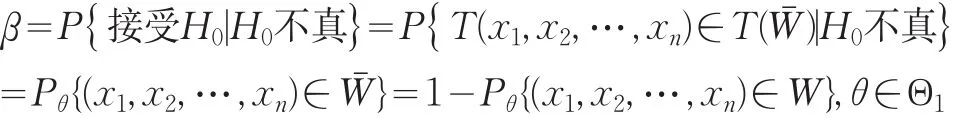
定义1设检验问题 H0:θ∈Θ0vs H1:θ∈Θ1的拒绝域为W，则样本观测值(x1,x2,…,xn)落入拒绝域W内的概率称为该检验的势函数，即

其中，Θ0,Θ1是参数空间两个互不相交的子集。

由两类错误的概率α、β与势函数的意义，可知它们之间的关系为：

由此可以看出，当α减小时，c也减小，而c的减小必导致β的增大；当β减小时，c会增大，而c的增大必导致α的增大。故得到两类错误的关系：

（1）在样本容量n一定时，α与β不能同时减小，α的减小必导致β的增大；β的减小必导致α的增大。

（2）要使α与β同时减小，则只有加大样本容量n，但又增加了检验的成本这在有些情况下又是不现实的。一般情况下控制α，使β尽量小。

定义2对检验问题 H0:θ∈Θ0vs H1:θ∈Θ1，如果一个检验满足对任意的θ∈Θ0，都有

则称该检验是显著性水平为α的显著性检验，简称水平为α的检验。

可见，显著性水平α就是用来控制犯第一类错误的概率的。最常见的选择是α=0.05，有时也选择α=0.1或α=0.01。

3 检验的p-值

假设检验的结论通常是简单的，在给定的显著水平α下，不是拒绝原假设就是接受原假设。然而有时也会出现这样的情况：在一个较大的显著水平下得到拒绝原假设的结论，而在一个较小的显著水平下却得到相反的结论。检验的 p-值是一个非常重要的概念，许多统计应用软件（如Excel、SPSS、EViews等）检验的输出结果都有检验的p-值(p-value)，可以根据 p-值和任意给定的显著性水平α直接作出接受或拒绝原假设H0的结论。

定义3在一个假设检验问题中，利用样本观测值能够做出拒绝原假设的最小显著性水平称为检验的p值。

引进检验的p值的概念有明显的好处：首先，它比较客观，避免了事先确定显著水平；其次，由检验的p值与人们心目中显著性水平α进行比较可以很容易做出检验的结论：

（1）如果α≥p，则在显著性水平α下拒绝H0；

（2）如果α＜p，则在显著性水平α下应保留H0。

设T为检验统计量，T0为由检验统计量得到的观察值，针对原假设和备择假设由T0为临界值确定的拒绝域为W0，检验的 p值为：

对于正态总体参数的u检验和t检验等对称的情形有：

其他检验的p值可以类似推出。

4 单侧检验的设定与拒绝域的确定

对于参数的单侧检验比较难于掌握的是原假设的设定和拒绝域的确定。单侧检验原假设H0的设定应遵从以下原则：

（1）H0不能轻易被否定；（2）等号包含在原假设H0内；（3）根据问题的背景来设定原假设。

由于原假设H0中参数的设定不是一个常数，而是一个范围。在H0成立的条件下，检验统计量在拒绝域内取值的概率只能通过不等式来确定，由此可以得到拒绝域是概率不超过α的更小概率得事件。

根据以下两种单边检验情况具体讨论：

①σ已知时的u检验

其中，tα(n-1)和 t1-α(n-1)=-tα(n-1)分别表示自由度为n-1的t分布的α和1-α的上侧分位数。

另外，单个正态总体方差的检验，两个正态总体均值差和方差比的检验都符合以上的结论，即拒绝域是概率不超过α的小概率事件。

5 区间估计与假设检验之间的关系

其他的各种情况同理，此不赘述。

[1]茆诗松，程依明等.概率论与数理统计教程[M].北京：高等教育出版社，2004.

[2]杨桂元.概率论与数理统计[M].北京：电子科技大学出版社，2004.

O212

A

1002-6487（2012）24-0013-02

安徽省高等学校人文社科基金重点项目；安徽财经大学教学研究项目（ACJYZD201213）

杨桂元（1957-），男，安徽萧县人，教授，研究方向：数量经济学。

刘德志（1982-），男，山东济宁人，讲师，硕士，研究方向：随机分析。

（责任编辑/亦 民）