冷轧带钢缺陷表面形状恢复新算法

杨永敏，李 戈，赵 杰

(哈尔滨工业大学机器人技术与系统国家重点实验室，150080哈尔滨)

目前，大多数表面缺陷检测系统只能检测二维信息，缺乏对三维信息的检测.三维信息不仅能提供更加直观的缺陷表达，同时更利于提高缺陷分类识别性能，因此对提取表面缺陷三维信息进行研究是十分必要的.三维重构是提取三维信息的有效手段，其中从阴影恢复形状［1］(Shape-from-Shading，SFS)的方法只需要单幅图像就能够完成三维重构，该方法已在很多领域得到了应用［2-3］.

SFS方法本身存在不确定性，解决该问题需从两方面考虑:正确光照模型的建立以及有效SFS数值算法的设计.光照模型主要有漫反射模型、镜面反射模型以及混合表面反射模型，其中朗伯体模型是理想的漫反射模型［4］，绝大多数SFS方法是基于该光照模型推导的，但是该模型与实际情况相差较大，因此提出了各种改进光照模型，如Oren-Nayar漫反射模型［5］，Phong镜面反射模型［6］、Torrance-Sparrow模型［7］以及Healey-Binford模型［8］等.SFS数值经典算法大致分为三类:优化迭代方法［9］、局部方法［10］和传播方法［11］等.近年来又出现了一些新的算法［12-14］，建立了更接近实际情况的光照模型，并引入新数学工具消除了SFS方法的不确定性.

本文根据冷轧带钢表面缺陷检测系统的自身特点，建立了改进的Oren-Nayar漫反射型光照模型，推导出了透视投影下相应的数学模型，利用高阶Lax-Friedrichs汉密尔顿函数与牛顿迭代相结合的快速扫描算法完成了方程的求解，最终通过实验验证了SFS方法的正确性和有效性.

1光照模型的建立

1.1 冷轧带钢表面缺陷检测系统分析

冷轧带钢表面缺陷检测系统放置在酸洗工艺之后，此时表面已经十分光滑洁净，其表面粗糙度大概在1.2 μm左右，其镜面反射率在60%左右.该检测系统采用中心波长为700 nm的高亮度LED线光源，光源发出平行光在带钢表面形成一条照度均匀的光带.图像采集器采用的是敏感波长为700 nm的线阵CCD，同时光学镜头中安装有690～710 nm的带通滤光片，从而确保不受外界环境光的影响.光路设计中使得入射角等于反射角.这种照明方式下，三维表面缺陷会产生漫反射，且随着表面形状的变化反射到采集传感器上的照度也会随之变化.照度的变化会使采集到的图像灰度发生变化，从而检测出三维缺陷.由上述分析可知，缺陷图像灰度变化是由漫反射变化引起的，因此利用SFS方法来恢复缺陷三维信息时采用漫反射光照模型.

1.2 改进光照模型

根据对冷轧带钢表面缺陷检测系统的分析，选择更接近实际情况的Oren-Nayar漫反射模型为原型进行改进，建立更加适合本系统的光照模型.

Oren-Nayar漫反射模型在建模过程中将观察方向也考虑在内，令光源方向为(θi，φi)，观察方向为(θr，φr)，并定义α=max［θr，θi］，β=min［θr，θi］，则在计算精度要求不高的情况下，当入射光强度为E0时，漫反射率为ρ的物体表面的辐照度为

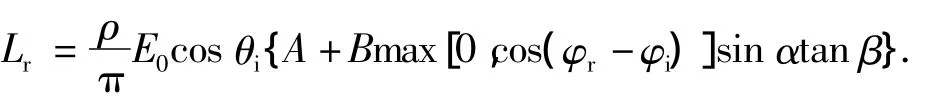
式中:A=1.0-0.5σ2/(σ2+0.33)，B=0.45σ2/(σ2+0.09)，σ为高斯分布的标准偏差，其大小由表面粗糙度决定.

在冷轧带钢表面缺陷检测系统中，光源为平行光入射，对于带钢表面的微面元来说，可将光源视为与其距离为r的点光源.图像采集传感器的光轴与光源位于同一平面之内，光源和图像采集传感器之间的夹角是一个固定的较小值，可以近似认为光源为前端照明，即认为光源位于图像采集传感器的光学中心.此时光源方向与图像采集传感器的光轴方向一致，应该有θi=θr=α=β=γ，同时考虑距离r所起到的衰减作用，则更适合本系统的光照模型具体表达式为

式中:η为常数，与光源的辐照度、带钢表面粗糙度和反射率参数、以及光学成像系统的各种参数有关，→L为光源方向，→N为表面法向.

2 数学模型的建立与求解

2.1 透视投影数学模型

在光照模型建立的过程中，假设图像采集传感器为透视投影，光源位于图像采集传感器的光学中心O，如图1所示，图中图像采集传感器由光学中心和成像平面组成，其焦距为f＞0.

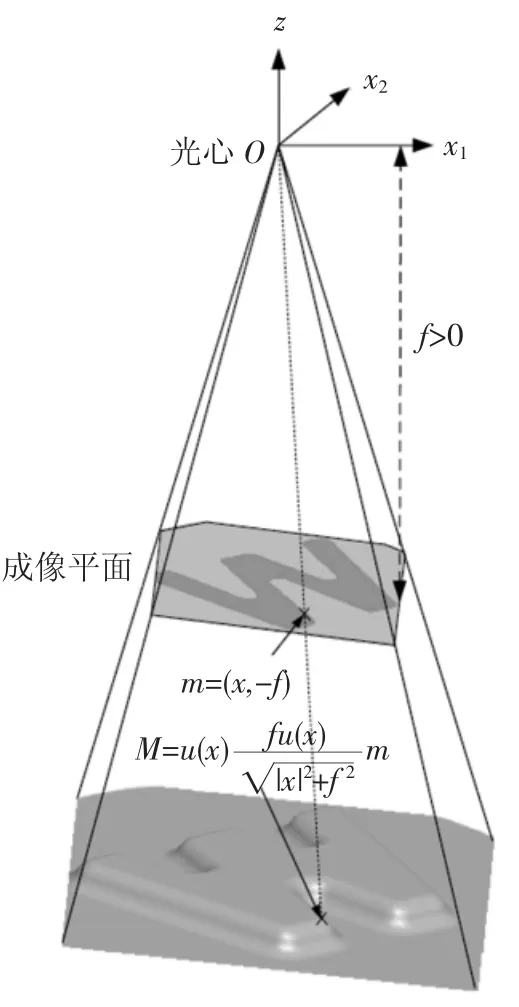
图1 透视投影成像模型

假设物体成像后由表面S来表达，并定义Ω为代表图像定义域的实数集R2的一个开集，为一个矩形区域，其大小代表了图像的尺寸，即:［0，X］×［0，Y］.用从集合Ω的闭包Ω到R3的映射来表示表面坐标x到物体表面S(x)的映射，即表面S的形状信息表示为

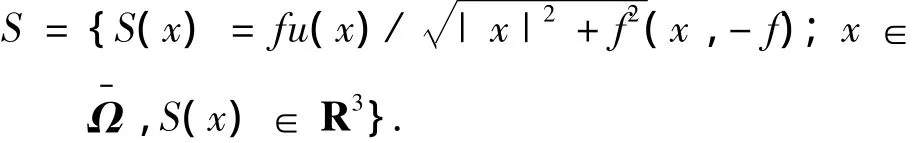
其中:u(x)为物体表面的连续函数，是未知量.对于这样的表面，任意一点S(x)的法向量可以表示为

此点的照明方向单位向量可以表示为

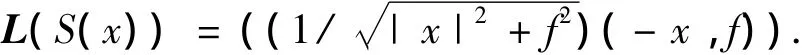
用Ⅰ(x)替代Ei/η，光源到物体表面的距离为r=fu(x)，带入到光照模型表达式中得到反射图方程:

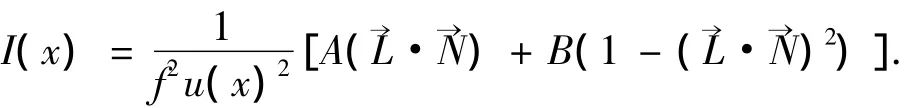
式中的(→L·→N)为光源方向矢量和表面法向矢量之间的内积，将其数学表达式代入可得

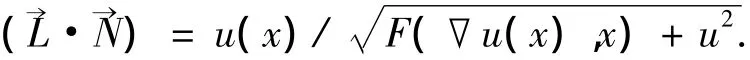
式中:

将式(1)带入反射图方程中，并利用变量代换方法进行简化，令v=lnu(x)，并通过整理可得

式(2)为静态H-J方程，该方程通常情况下不存在经典确定解.根据黏性解的概念，为了确保该方程具有唯一解，需要给定Dirichlet边界条件［15］，得到如下的方程组:

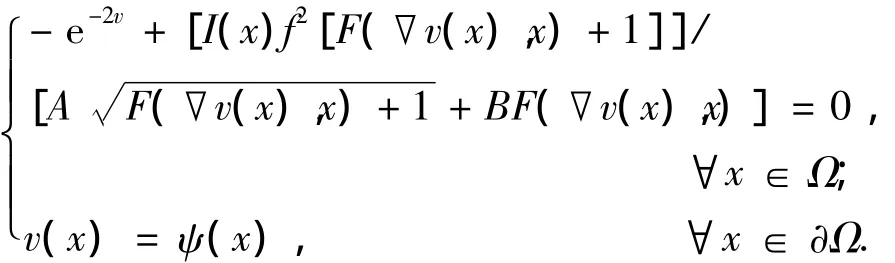
该方程组中的H-J方程是非凸的，而Lax-Friedrichs快速扫描方法不用考虑汉密尔顿函数的凸凹性，且计算简单，速度快，因此用该方法对方程组进行求解.

2.2 高阶Lax-Friedrichs快速扫描方法

Lax-Friedrichs快速扫描策略是Kao等［16］提出的基于Lax-Friedrichs单调数值汉密尔顿函数的快速扫描方法，可用来近似任何空间维度中的任意静态H-J方程的黏性解.高阶快速扫描的本质就是利用高阶加权本质无振荡格式来进行偏导数的近似，同时结合Lax-Friedrichs单调数值汉密尔顿函数以及Guass-Seidel迭代来完成4个方向上的快速扫描.

考虑二维空间中如下的静态H-J方程组:

其中:Ω为R中的计算域，Γ是Ω的边界子集，

p=∂φ/∂x，q=∂φ/∂y，汉密尔顿函数H为一个非线性的Lipschitz连续函数.应用到该静态方程组的Lax-Friedrichs单调数值汉密尔顿函数为

其中σx和σy为人工黏性因子，且σx≥max｜∂H/∂p｜，σy≥max｜∂H/∂q｜，偏导数p和q用高阶加权本质无振荡格式来近似.下面以三阶加权本质无振荡格式来进行分析，其插值模板如图2所示.

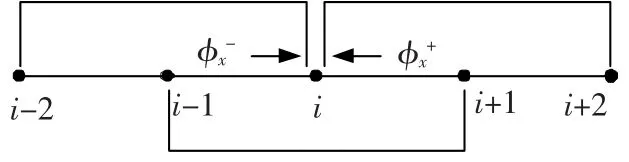
图2 三阶加权本质无振荡策略模板

网格点(i，j)处前向和后向差分p±的三阶加权本质无振荡近似表示为［17］

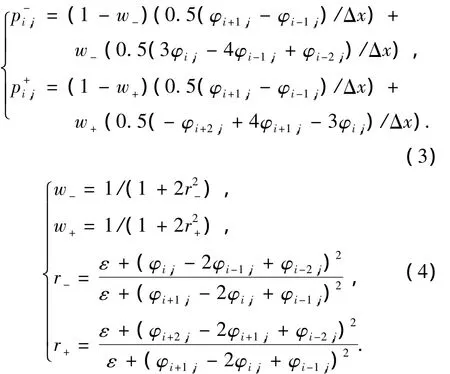
其中ε为防止分母为零的正常数，后续的计算中选择10-5.类似可以推导出网格点(i，j)处q±的三阶加权本质无振荡的近似表示.

将式(3)、(4)带入Lax-Friedrichs单调数值汉密尔顿函数，经过整理得静态H-J方程组的数值粘性解的迭代计算公式为

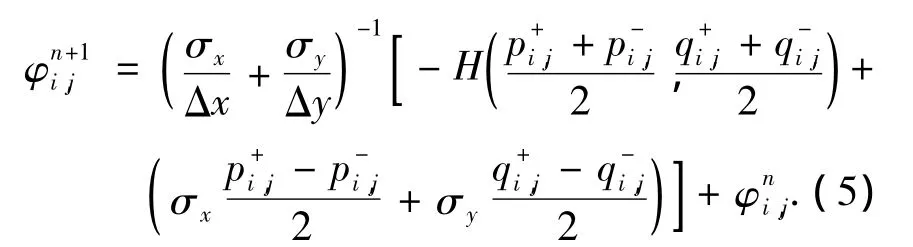
其中，φ是φi，j的更新函数值为同一网格点上当前的函数值.式(5)右侧的偏导数近似值未使用上标，其上标由Gauss-Seidel迭代的交替扫描方向决定，确保式中的，总是使用函数φ在网格点上的最新当前值来计算.

2.3 基于快速扫描的SFS算法

根据改进的光照模型推导出的数学模型为静态H-J方程，为了应用高阶Lax-Friedrichs快速扫描方法进行求解，将其改写成如下的形式:

式中:

首先对图像区域Ω进行离散化处理，假设图像的大小为M×N，可以将图像区域Ω离散化为大小为M×N的矩形网格区域，网格上的点即为像素点{(xi，yj)，i=1，2，…，M;j=1，2，…，N}，均一化网格的大小等同于像素的大小(Δx，Δy)，实际计算中认为Δx=Δy.每个像素点的高度值是未知的，离散化的目的就是要获取每个像素点上高度值的近似解Vi，j=v(iΔx，jΔy).

根据高阶Lax-Friedrichs扫描策略，可以得到近似解的迭代更新公式如下:

对于Vi，j来说，式(6)是非线性的，需要使用牛顿迭代法对其进行求解.

令t=Vi，j，a=-1/(σx/Δx+σy/Δy)，且将式(6)的左侧用b表示，则上式转化为

函数f的一阶导数为

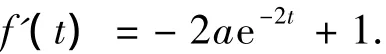
令初始值t0=Vni，j，利用如下的公式来计算t的更新值

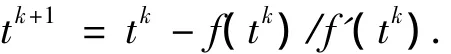
较少迭代步骤后，就能够完成迭代公式的更新计算.

迭代更新公式中的黏性因子σx和σy按照参考文献［18］中所提到的非线性黏性因子的方法进行确定:

综上所述，整个算法具体实现步骤如下.

1)初始化.给定图像Ⅰ(x，y)，并设置图像中边界点的高度值，根据边界条件外推计算附近点的高度值，这些高度值在后续的迭代运算过程中保持不变.为其他像素点的高度值分配一个大的正值C，使其大于所有像素点对应的高度值的最大值.

2)交替扫描.在第n+1次迭代中，除了高度数值固定的像素点外，其他所有像素点均按照迭代更新公式来计算高度值Vni，+j1.当且仅当得到的值小于上一次迭代计算值Vn i，j时，将像素点的高度值Vi，j更新为Vni，+j1.每个迭代过程分别从4个不同的扫描方向上进行:(1)i=1∶M，j=1∶N;(2)i=M∶1，j=1∶N;(3)i=1∶M，j=N∶1;(4)i=M∶1，j=N∶1.

3)更新边界条件.每次扫描之后，更新计算域外部虚拟点的高度数值的计算公式如下［16］:

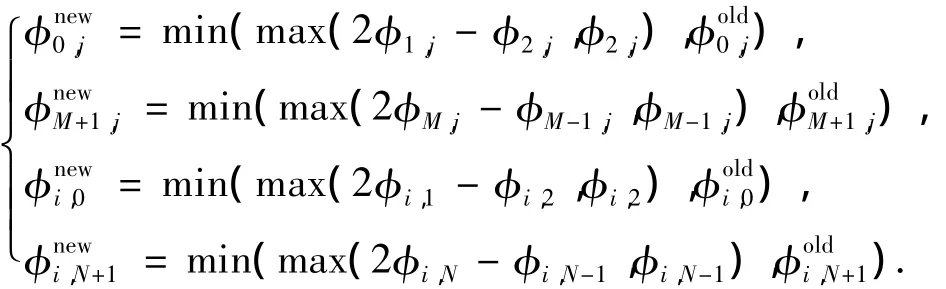
对于表面缺陷图像，其计算域边界往往属于正常部分，像素点高度值是固定不变的，可以认为其计算域外部虚拟像素点的高度也是固定的，因此在实际运算中边界条件的更新可以省略.

4)计算结束.如果‖Vn+1i，j-Vni，j‖≤δ(δ为给定的收敛阈值，表示连续两次函数值计算结果的差异)，或者迭代次数到达给定的次数，则算法结束并输出像素点高度函数的数值.

3 实验分析

下面对人工合成图像以及实际表面缺陷图像分别进行实验，验证改进光照模型的正确性，以及所采用算法的有效性.实验运行的硬件条件为Intel Core i5 760 2.8 GHz，RAM为2 GB.下面对基于SFS方法的三维重构实验进行详细分析.

3.1 人工合成图像实验

选择最通用半球和花瓶合成图像来进行实验.合成图像采用本文提出的基于透视投影的改进光照模型，图像按照如下的参数生成:光源位于光心位置(0，0，0)T，图像采集传感器的焦距为100像素，取参数σ=0.195.

半球人工合成图像的三维形状生成公式为

花瓶人工合成图像的三维形状生成公式为

按式(7)、(8)并结合反射图方程，生成分辨率为120×120的合成图像.由于基于透视投影的反射图方程具有伸缩不变性，因此每次迭代运算后对得到的高度函数进行归一化处理，迭代30次后得到的半球和花瓶的三维形状重构结果如图3、4所示.

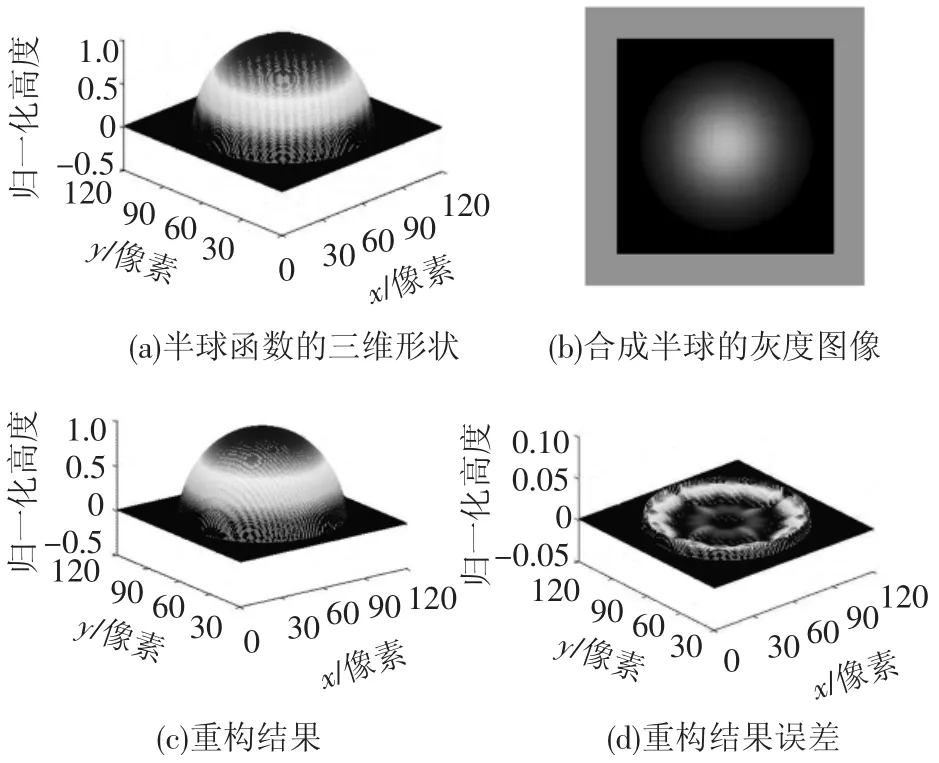
图3 合成半球的三维重构结果

图4 合成花瓶的三维重构结果

同时引入高度平均误差(ME)、高度均方根误差(RMSE)以及CPU运行时间等标准对结果进行分析和评价.图5、6分别为合成半球和花瓶重构的三维形状高度平均误差和均方根误差随迭代次数的变化情况.表1给出了迭代30次时重构结果.

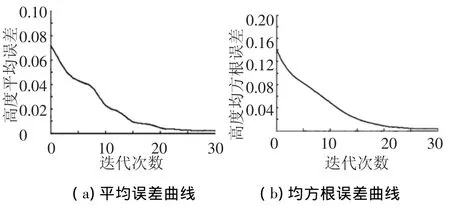
图5 合成半球的三维重构结果

表1 归一化高度平均误差、均方根误差及运行时间

由以上图标分析可知，该方法能够获得较高精度的重构结果.实验过程中发现，迭代次数超过20次，高度的平均误差和均方根误差的下降不再明显，基本保持不变，这应该是数值计算误差引起的，包括图像离散化以及差分近似计算引起的误差.

3.2 实际表面缺陷图像实验

选择孔洞、夹杂两种表面缺陷进行实验，系统的参数设置如下:光源位于光心位置(0，0，0)T，图像采集传感器焦距为20 mm，取参数σ=0.428，设置迭代次数为20作为结束条件.对表面缺陷分别在朗伯体反射模型以及本文提出的改进光照模型下进行实验，图7为表面缺陷灰度图像，实验结果如图8和9所示.为更清晰地表达三维重构后的结果，孔洞缺陷本来是凹陷的，将其进行翻转以凸起的形式来表达.

图7 表面缺陷图像

图8 孔洞缺陷三维重构结果

图9 夹杂缺陷三维重构结果

获取冷轧带钢表面缺陷的确切三维高度信息在目前的实验条件下是比较困难的，在无法进行定量分析的情况下，只能从视觉效果上对它们进行对比分析.由图9中可以明显看到，基于改进光照模型恢复的三维形状要比基于朗伯体光照模型恢复的三维形状更加接近于缺陷的实际形状，表明改进的光照模型能够消除凸凹二义性，而通用的朗伯体模型无法做到这一点.总之，基于改进光照模型和高阶Lax-Friedrichs和牛顿迭代相结合的快速扫描SFS算法是正确且有效的，能够完成实际表面缺陷的三维重构.

4 结论

1)在对冷轧带钢表面缺陷检测系统的光路布置以及Oray-Nayar漫反射模型深入分析的基础上，根据光路布置对该漫反射模型进行了合理简化，同时考虑到光源到物体表面距离所起到的衰减作用，提出了一种适用于表面缺陷检测系统的改进光照模型，并在实验中得到了验证.

2)将透视投影模型与改进光照模型相结合，推导出了透视投影下的反射图方程，完成了数学模型的建立，针对该反射图方程，提出了一种高阶Lax-Friedrichs汉密尔顿函数和牛顿迭代相结合的快速扫描算法来实现该方程的求解.

3)利用人工合成图像和表面缺陷图像进行了实验验证，人工合成图像实验结果表明本文所设计的三维重构算法能够获得较高的重构精度，同时表面缺陷图像实验结果进一步验证了改进光照模型以及改进高阶Lax-Friedrichs快速扫描算法的正确性与有效性，充分说明了利用基于SFS原理的三维重构算法能够有效的实现表面缺陷的三维重构.

［1］ZHANG Ruo，TSAI P S，EDWIN J，et al.Shape from shading:a survey［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1999，21(8):690-706.

［2］CARTER C N，PUSATERI R J，CHEN Dongqing，et al.Shape from shading for hybrid surfaces as applied to tooth reconstruction［C］//Proceedings of 2010 IEEE 17thInternational Conference on Image Processing.Hong Kong:IEEE Computer Society，2010:4049-4052.

［3］赵辉煌，周德俭，黄春跃，等.基于SFS原理的SMT焊点表面三维重构技术研究［J］.计算机科学，2009，36(7):288-291.

［4］HORN B K.Height and gradient from shading［J］.International Journal of Computer Vision，1990，5(1):37-75.

［5］OREN M，NAYAR S K.Generalization of lambert’s reflectance model［C］//Proceedings of the 21stAnnual Conference on Computer Graphics and Interactive Techniques.Orlando，USA:ACM，1994:239-246.

［6］PHONG B T.Illumination for computer generated pictures［J］.Communications of the ACM，1975，18(6):311-317.

［7］TORRANCE K E，SPARROW E M.Theory for off-specular refelction from roughed surfaces［J］.Journal of the Optical Society of America，1967，57(9):1105-1114.

［8］HEALEY G，BINFORD T O.Local shape from specularity［J］.Computer Vision，Graphics and Image Processing，1988，42(1):62-86.

［9］FRANKOT R T，CHELLAPPA R.A method for enforcing integrability in shape from shading algorithms［J］.IEEE Transactions on PAMI，1988，10(4):439-451.

［10］LEE C H，ROSENFELD A.Improved methods of estimating shape from shading using the light source coordinate system［J］.Artificial Intelligence，1985，26(2):125-143.

［11］DUPUIS P，OLIENSIS J.Direct method for reconstructing shape from shading［C］//Proceedings of the image Understanding Workshop.San Diego，CA，USA:Morgan Kaufmann Publ Inc，1992:453-458.

［12］ZHANG Li，YIP A M，TAN C L.Shape from shading based on lax-friedrichs sweeping and regularization technique with application to document image restoration［C］//Proceedings of 2007 IEEE Computer Society Conference on CVPR.Minneapolis，MN，USA:IEEE Computer Society，2007:1180-1187.

［13］YUEN S Y，TSUI Y Y，Chow C K.A fast marching formulation of perspective shape from shading under frontal illumination［J］.Pattern Recognition Letters，2007，28(7):806-824.

［14］PARDOS E，CAMILLI F，FAUGERAS O.A unifying and rigorous shape from shading method adapted to realistic data and applications［J］.Journal of Mathematical Imaging and Vision，2006，259(3):307-328.

［15］BARDI M，CAPUZZO-DOLCETTA I.Optimal control and viscosity solutions of hamilton-jacobi-bellman equations［M］.［S.l.］:Birkhäuser Boston，1997:1-23.

［16］KAO C Y，OSHER S，QIAN J.Lax-friedrichs sweeping scheme for static hamilton-jacobi equations［J］.Journal of Computational Physics，2004，196(1):367-391.

［17］ZHANG Yongtao，ZHAO Hongkai，QIAN Jianliang.High order fast sweeping methods for static hamilton-jacobi equations［J］.Journal of Scientific Computing，2006，29(1):25-56.

［18］刘瑞玲，韩九强.透视投影下的镜面反射表面形状恢复新算法［J］.西安交通大学学报，2009，43(2):6-10.