柔性生产中人员配置模型及其调度算法

高 丽，徐克林，朱 伟，童科娜

(1.同济大学机械工程学院，201804上海;2.上海理工大学图书馆，200093上海)

针对柔性企业的人员优化配置问题，国内外学者已进行了大量的研究并取得了一定的研究成果［1-3］.从优化目标来看，最小化最大完工时间［4-5］、合理的人工配置以及最佳作业排序［6-8］被作为优化调度的目标;但迄今为止，将这些目标结合起来进行多目标优化的研究较少.

由Bhaskar等［9］提出的MIP(mixed integer programming)和Suer［10］提出的两阶段启发式算法，以及后来Kuo等［11］应用这两种方法对具有不同技能的人工分配问题的研究，均是以最小化最大完工时间为优化目标研究人工配置问题的，也就是只考虑了“多少人工作”(人员配置)的问题，而没有考虑“这些人何时工作”(作业排序)的问题［12］.

本文综合考虑了这两个优化目标——合理的人员配置和最佳作业排序，提出了一种两级递阶结构的混合优化算法［13］.第一级，基于遗传算法和动态规划法求解多种人工分配方案及对应的最优作业工时;第二级，基于遗传算法和模拟退火算法求解作业排序问题.与单目标算法结果对比表明，本文提出的算法有效，具有较好的鲁棒性.

1 人员配置问题及模型建立

1.1 问题描述

针对柔性生产企业，有n个工件(j1，j2，…，jn)按方向一致的加工路线依次通过s个工位，该作业由队伍B完成.假设任意两道工序间存在有限的存储能力(即被加工工件在两道工序间等待时间受限)，每道工序的工人工作熟练度相当且每个工件在每道工序的加工时间已知.优化目标是要确定一个调度:确定最合理的人工分配方案和作业调度方案，以使作业总完工时间最短.

1.2 模型参数和决策变量

设P={i=｜i=1，2，…，n}为工件集合;S={j=｜j=1，2，…，r}为工位集合;B={k=｜k=1，2，…，K}为人员集合;L为生产线集合;Bk为总人工数;gik表示分配到i工位的人工单位累计数;tsijk为工件在工序k的开工时间，tijk为工件i在工序k的加工时间;teijk为完工时间，Tik为工件加工总时长.

决策变量为:0≤Xil≤1，表示产品i分配到生产线l上.

1.3 数学模型

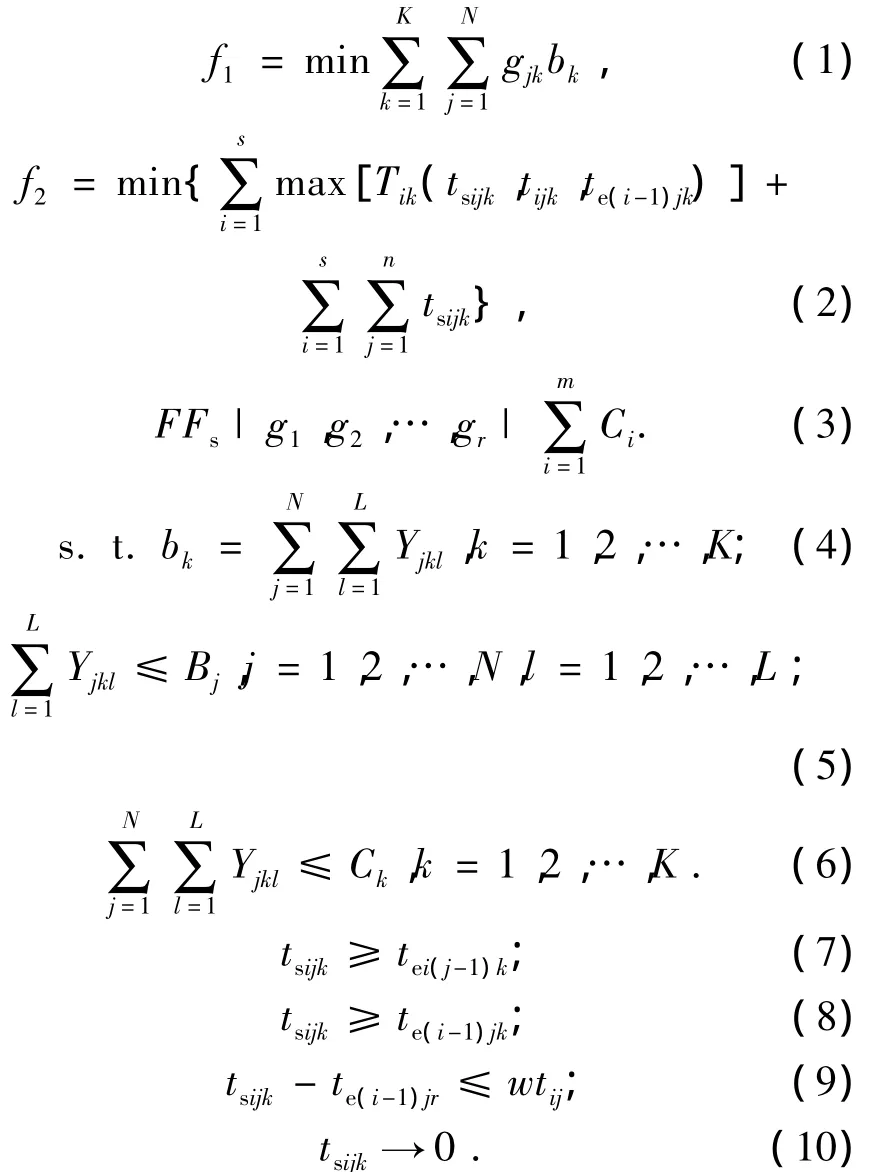
式中，目标函数(1)为最优人工分配方案.目标函数(2)为最佳作业排序对应的最小完工时间.式(3)为将两个优化目标组合的表示方式，Fs｜g1，

mg2，…，gr｜表示人工决策集合是工件总完工时间的不减函数.式(4)～(10)为约束条件，式(4)为中各工位对应的人工总数.式(5)、(6)表示各工位人工约束.(7)～(10)表示作业排序时间约束.

1.4 模型求解策略

该数学模型主要求解两个问题:确定最合理的人工分配方案和最佳作业排序.由于人工的固定费用远大于作业运行费用，所以将柔性生产线的优化调度求解过程分为两级:第一级，确定最佳人工分配问题方案.第二级，在给定各工序合理的人员分配前提下决定各工件的加工顺序(排序问题).

2 算法设计

2.1 人工分配优化算法

首先，将作业进行归类分组.一般将加工流程分解为两个层次——子作业层和父作业层.采用遗传算法求解子作业层中多种人工分配方案及对应的最优作业工时，然后将子作业层视为父作业层的一个阶段采用动态规划法获取整个作业流程的最优工时.

2.1.1 遗传算法求解人工分配方案及最优作业工时

将遗传算法用于子层并联作业的人工分配问题关键是采用有效的编码和解码方式以及适当的交叉、变异操作.遗传算法对种群重复地进行选择、交叉、变异等基本遗传操作.不断产生出比父代更适应环境的新一代种群，直到满足要求条件为止.

1)个体编码.本文采用直接编码的方式，以工序为对象.将分配工人数作为码值这种编码方法可避免同一工人在不同作业中的操作运算产生死锁现象.以3个工人在3项作业中的2种分配方案为例，结果见表1.

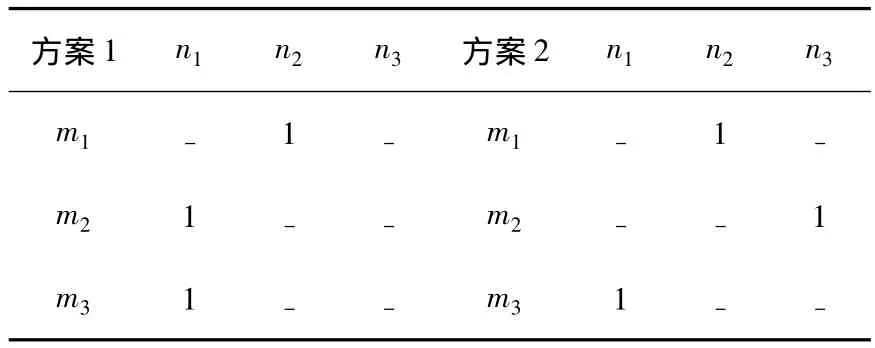
表13 个工人在3项作业中的两种分配方案

获得染色体编码如表2(以两位二进制码构成基因座，根据实际作业工人数调整二进制码位)

表2 染色体编码

2)群体规模选择.合适的群体规模对遗传算法的收敛具有重要意义.群体太小难以求得满意的结果，群体太大则计算复杂.根据经验，群体规模一般取10～150.

3)适值函数.按照并行作业工人分配理论，如部分作业先不执行，待部分作业完工后再进行等考虑最复杂的情况，假设n项并行作业经过m个过程完成，其中k表示第k个作业组内同时开工的作业项目，得到适值函数为

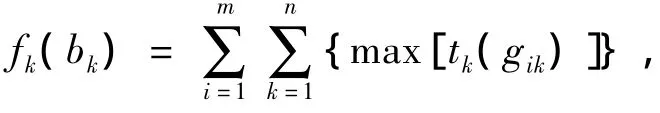
其中，1≤m≤n;1≤i≤m;k∈［a，m］.

本文模型选取m=1，即n项作业单独作为一项工序优化求其最短工时.

4)选择.选择是用来确定重组或交叉个体，以及备选个体将产生多少个子代个体.若有m个个体，其中某个个体i，其适值为fi，则其被选择的概率表示为

5)交叉与变异.交叉在遗传操作中起核心作用，交叉概率较大可增强遗传算法开辟新搜索空间的能力.本文采用循环交叉操作(选择3个码串为一基点进行相互调换).变异主要是为保证算法的局部随机搜索能力和维持种群的多样性.当遗传算子在接近最优解时，变异可以加速向最优解的收敛.本问题的变异算子采用如下方法:在随机选中染色体(个体串码)中首先针对一个基点(即作业人员)增加一个单位，然后采用随机原则，任选其他一个基点减少一个单位，既符合变异保证在全局范围内又保证了变异的前提条件即作业人员的总数不变，但对个体串码而言实现了重排序操作.

2.1.2 动态规划法求取作业流程的最优工时

引入动态规划法是将前面通过遗传算法所获得的决策作为一个阶段决策，不管前面的决策如何，要将余下的诸决策必须构成最优策略;因此可将多阶段决策问题的求解过程看成一个连续递推过程，由后向前逐步计算［8］.

动态规划模型中设置了几个必要变量:决策变量bk，以及决策集合FFs｜g1，g2，…，gr｜，本文通过遗传算法首先对子层并联作业交叉变异优化，获得不同人工分配方案及对应的最优工时后，将其作为一个阶段与该工序内其他的独立作业构成一族同类型的子问题，最终得出人工分配的最优指标函数.

2.2 作业排序优化算法

确定了人工分配方案下的作业排序问题是典型的job-shop调度问题，近年来，运用遗传算法解决这类问题的例子很多，本文采用遗传模拟退火算法(GASA)［14］.以下简要说明该混合算法的特性和关键步骤.

2.2.1 算法特性分析及关键步骤处理

2.2.1.1 适应度函数值

以式(2)作为目标函数，需要先计算工序i中各工位的总加工时间Tik，然后从中找出最大值，各工序的最大值求和;在式(2)中，目标函数是使得f(t)最小化.取目标函数适应度值为该个体的目标函数值的倒数:

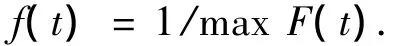
2.2.1.2 初始温度

令波尔兹曼常数为1，初始温度

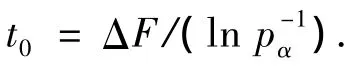
式中，ΔF=Fmax-Fmin，Fmax和Fmin分别为初始种群p(0)中个体的最大和最小目标函数值;pα为劣解接受概率.

2.2.1.3 选择、交叉、变异

(a)选择.为了确保适应度大的个体能被保留到下一代种群中，采用确定式采样来选择复制染色体.先计算每个个体在下一代种群中期望生存的数目然后取各N的整数值作为该个体在下一代种群中出现的数量，由此可确定出下一代种群中符号⎿」表示取整;最后按照各Ni(i=1，2，…，p)的小数部分对个体降序排列，顺序取前个个体补充到下一代种群，由此共得到p个新染色体组成一组新种群.

(b)交叉.采用两两随机分组交叉方式.各染色体产生交叉的概率pc设为一个固定值，比如pc=0.60，当产生0～1之间的随机数值p＜pc时，发生交叉.交叉只发生在同一工序的染色体之间，确保基因变化的合法性.交叉点随机选择在1～n之间的任意一点，交叉点之后的全部基因进交叉.

(c)变异.为了保证种群的稳定性，选择变异概率pm≤0.001，采用循环方式过滤种群的每个基因，当产生的随机数值p＜pm时，将当前基因的整数部分随机增或减1，只要始终确保每个基因整数部分的变化在合法的范围内即可.

2.2.1.4 局部搜索过程

(a)初始化马尔可夫链长和局部最优解保持不变的次数q为0.令局部最优解s*=s＊＊当前状态为s.

(b)从当前状态s产生一个新解s'，计算二者目标函数值的差值Δc'=c(s')-c(s).

(c)若Δc'≤0，则接受s'作为当前状态，令s＊＊=s'，q=0;若c(s*)＞c(s')，则令s'=s*;若Δc'＞0，则按照事先定义的pa接受s'作为当前状态;若s被接受，则令s'(l+1)=s'，q=q+1，否则仍令s'(l+1)=s'(l).

(d)令l=l+1，若满足算法终止条件(q＞qmax或l＞lmax)，则执行步骤(e);否则转步骤(b).

(e)用s＊＊代替s.

2.2.1.5 精英策略

为了防止丢失最优解，若c(s*)＞c(s＊＊)，则令s*=s＊＊，否则用s*替换临时种群中的最差个体.

2.2.2 算法实现步骤

Step1产生初始种群p(0).

Step2计算p(0)中各个体的适应度值，分别记全局最优解和最优目标函数值为s*和c*，确定初始温度t0.令进化代数g=0.

Step3若进化代数超过设定的最大值w，则输出s*和c*，算法结束;否则继续执行以下步骤.

Step4进行遗传操作(选择、交叉、变异).

Step5分别以经过以上步骤得到的临时种群中的每个个体S为起点，根据Metroplis抽样准则进行局部搜索.

Step6评价经过以上步骤后所得临时种群p'(g)中的所有个体，更新s*和c*.

Step7保存最优解.

Step8令g=g+1，tg=αtg-1(α为冷却速度)，转步骤3.

3 案例分析

3.1 求解最优人工分配方案

运用算法对某食品加工厂的检验和包装流程进行求解.现有5类型号产品，分别为A、B、C、D、E.工位额定人数和工时如表3所示.

由表3可知该工序共有6项作业.其中作业1～6可归为父层并联作业;作业3由3项作业组成，属于子层(由虚框标出)，子并联作业完成后.再执行4，5，6作业.故该工序的各项作业属于组合并联作业.现已知该厂安排40名员工分组进行该工序作业，要求对各班组进行合理分配，使完成该工序的作业时间最短.

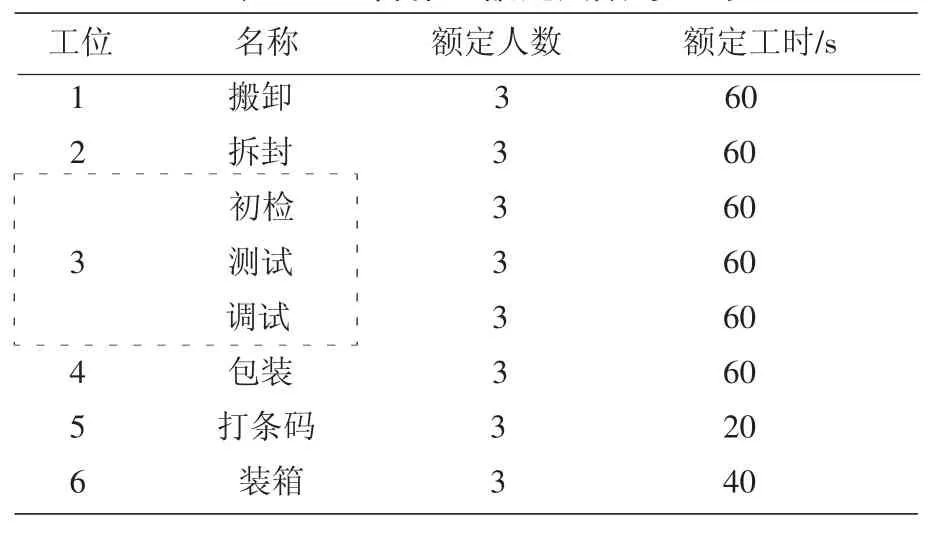
表3 %%组合作业额定人数与工时

优化步骤一:针对第5层作业采用遗传算法进行优化，计算其不同人工分配方案及对应的最短工时.由表3获得已知数据，设置种群规模为20，交叉概率0.8，进化次数100，变异概率0.1，由VISUAL BASIC软件编制程序得到优化结果.将班组分为2组时，人员分配最合理同时完工时间也较小.

优化步骤二:在获得子层作业的不同分配小组方案及对应最短作业工时的基础上，采用动态规划计算父层的最优工时及人工分配方案，将第3子层作业视为第3阶段，得到各阶段的tk=tk(gk).由适应度函数公式计算可知:当k=4时，4≤bg≤7以此类推，当k=2时，得到该组合作业的最短完工时间是450 s，同时得到最短完工的作业人工分配方案:g1=2，g2=2，g3=(1，1，1)，g4=2，g5=1，g6=2.

3.2 作业排序优化

人工分配方案确定后，假定该加工线班次生产计划为:4A、5B、5C、6D、7E.各工位对不同型号产品的作业时间见表4.

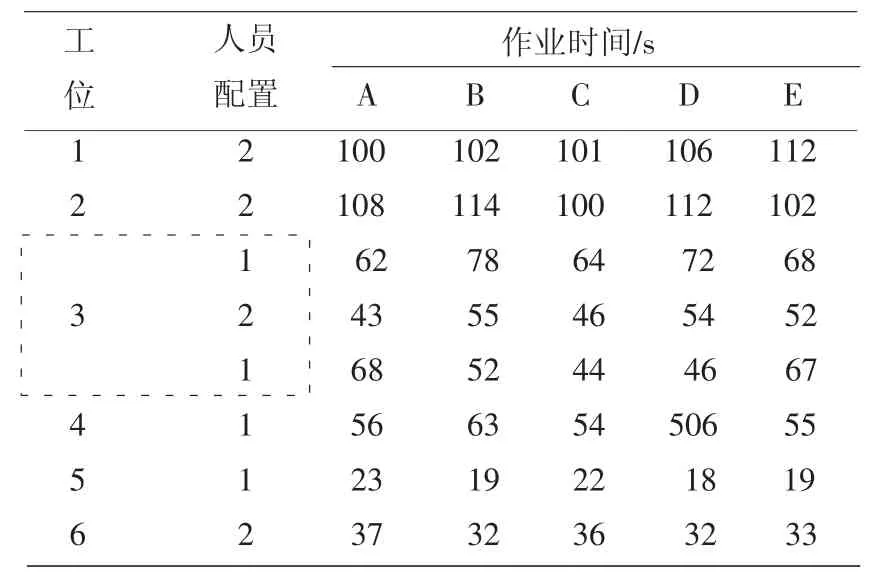
表4 %%加工线组成及加工时间

以最小化最大完工时间为优化目标，采用GASA混合算法求解该生产线调度问题，算法采用C++编程，经过算法灵敏性计算试验，选择的算法参数值为:v=50，pc=0.85，pm=0.20，pa=0.50，ps=0.60，qmax=3，lmax=8，α=0.95，gmax=20.其他计算数据见具体的应用问题.表5列出了该厂在各工位等额分配人员采用不完全混排的方法安排每班的加工任务，共有36种排列顺序，为节约篇幅，表中只列出了5种排列的计算结果，同时与本文提出的混合算法运行25次的最优排序结果进行了比较.

表5 作业排序结果比较

从表5可以看出，应用本文提出的混合算法进行排序求解，可以缩短加工时间3.8%～8.6%，CPU时间为902 s.若采用最小生产集合的方式组织生产，所得的结果与不采用重复生产最小生产集合的方式的结果是相同的，但是CPU计算时间仅需要325 s，优化效率有显著提高.

4 结束语

本文所研究的柔性生产中人员配置问题属于有约束混合离散优化问题，因此难以针对整个过程建立统一的优化模型.以作业人工分配和作业排序为优化目标，采用混合遗传算法分阶段求解该问题，仿真实验说明了该方法的有效性.同时也为生产系统调度中的诸多组合优化问题提供了一个具有前景的新方法.

［1］ERTAY T，RUAN D.Data envelopment analysis based decision model for optimal operator allocation in CMS［J］.European Journal of Operational Research，2005，164(3):800-810.

［2］ISLAM R，RASAD S M.Employee performance evaluation by the AHP:A case study［J］.Asia Pacific Management Review，2006，11(3):163-176.

［3］YANG T，CHEN M C，HUNG C C.Multiple attribute decision-making methods for the dynamic operator allocation problem［J］.Mathematics and Computers in Simulation，2007，73(5):285-299.

［4］BRUCKER P，HEITMANN S，HURINK J.Flow-shop problems with intermediate buffers［J］.OR Spectrum，2003，25(4):549-574.

［5］RONCONI D P.A note on constructive heuristics for the flow-shop problem with blocking［J］.International Journal of Production Economics，2004，87(1):39-48.

［6］WANG Ling，ZHEN D Z.An effective hybrid heuristic for flow-shop scheduling［J］.International Journal of Advanced Manufacturing Technology，2003，21(1):38-44.

［7］PONNAMBALAM S G，MOHAN R M.A GASA multiobjective hybrid search algorithm for integrating lot sizing and sequencing in flow-line scheduling［J］.International Journal of Advanced Manufacturing Technology，2003，21(6):126-137.

［8］SAWIK T.Mixed integer programming for scheduling flexible flow lines with limited intermediate buffers［J］.Mathematical and Computer Modeling，2000，31(13):39-52.

［9］BHASHKAR K，SRINIVASAN G.Static and dynamic operator allocation problems in cellular manufacturing systems［J］.International Journal of Production Research，1997，35(12):3467-3481.

［10］SUER G A，BERA I S.Optimal operator assignment and cell loading when lot-splitting is allowed［J］.Computers and Industrial Engineering，1998，35(3):431-434.

［11］KUO Y，YANG T.Optimization of mixed-skill multiline operator allocation problem［J］.Computers and Industrial Engineering，2007，53(3):386-393.

［12］SEN C G，CINAR G.Evaluation and pre-allocation of operators with multiple skills:A combined fuzzy AHP and max-min approach［J］.Expert Systems with Applications，2010，37(3):2043-2053.

［13］王笑蓉，吴铁军.基于Petri网仿真的柔性生产调度［J］.浙江大学学报，2004，38(3):286-291.

［14］王炳刚，混流加工/装配系统集成优化研究［J］.机械工程学报，2010，46(17):114-120.