谈中职数学公式的教学

黎东辉

（湛江财贸学校，广东 湛江 524094）

在中专数学的学习中，很多学生会觉得数学公式是抽象的、枯燥无味的。就读中职的学生一般是英语和数学这些课程比较差，而中职数学这门课程又与初中数学又有密不可分的联系。如何让学生能从怕学习数学到喜欢数学，是中职数学教师面临的一大难题。而这一学科留给学生太多的恐惧，留给教师许多的无奈。数学公式是解题的工具，深刻理解并准确掌握数学公式是学好数学的第一关。如何在数学公式的教学中,让学生乐学，让学生易学，本文从以下几点谈一下中职数学公式的教学。

1 数学公式的引入

公式的引入是发展学生思维的起点，是培养学生学习、探索知识的首要环节。在引入公式前，学生在等待老师激发他们学习的兴趣，这时候教师应创造学习的乐趣，吸引学生的注意力。公式的引入如果生动、新颖，将增强学生学习的信心。可是在教学中如果直接使用“平铺叙事式”方法，开门见山地直接到公式的引入教学中，学生很难有兴趣学好。近代教育学家斯宾塞指出：“教育要使人愉快,要让一切教育有乐趣”。兴趣是最好的老师,在数学公式的教学中,如果能够充分调动学生的兴趣,往往就能取得良好的教学效果。中职数学与普通高中要求不同，考虑到中职学生的数学基础比较薄弱，上课注意力有时分散、不够集中，中职数学公式的教学主要采用以下几种引入方法。

1.1 数学故事引入

例如在讲授等差数列的前n项求和公式时，我就利用德国数学家高斯小时候的计算数列“1+2+3+…+100”的故事，启发学生思考奇数项“1+3+5+…+99”和偶数项“2+4+6+…+100”的答案，进而猜想、证明出一般等差数列的前n项和公式。在讲授等比数学的前 n项和公式时，利用一个国际象棋棋盘格数 64个格数的小故事，引入等比数列的计算。通过这些耳熟能详的小故事，它们本身蕴含着生动的人文事故事背景，让学生在思考一个开放性的数学问题上，学会分析数学问题、解决数学问题，从而提高兴趣学习数学公式。

1.2 发现式引入

公式反映了数学对象的属性之间的关系，是数学对象高度概括的具体表征。发现式引入公式，可采用设计实验、设计小问题等方法引导学生思考、分析、归纳。如在数列的通项公式这一内容中，可从例题中项数的规律，指导学生观察特征，分析特点，从而推导出通项公式的正确答案。又如非空集合真子集个数的计算，可以让学生从集合元素个数分别是 2，3，4时，真子集个数就是个，学生就会主动探索出元素个数是n个时，真子集个数的正确结论了。

1.3 反例式引入

由于学生学习时的联想作用，常常使学生产生了一些错误的猜想，以至把错误的信息当作正确的公式去使用，因此有些数学公式教学时用反例式引入，能达到更好的教学效果。例如学生都非常熟悉的特殊角的三角函数值，在讲解和角公式先让学生判断是否成立，显然是不成立的，这就说明了在这种反例式的公式教学的引入的过程中，使学生认识到数学就是在猜想、证明、犯错误、修正错误中发展进化的，从而激发了学生的非常规思维，再引导他们得到了正确的结论。

1.4 课件辅助引入

计算机技术的飞速发展，给了中专数学带来了许多新的活力。在上课的过程中，精彩的FLASH动画、专业的PPT演示、随意变化的几何画板等计算机教学手段更容易激发学生的兴趣与专注，这些都是传统教学所不能达到的。教师可以使用教材中辅助的课件或者上网搜索素材，用先进的计算机教学来替代传统的黑板授课。如在讲授正弦型三角函数图像时，计算机在处理图像的平移、拉伸、缩短时，生动而且形象，传统的粉笔作图与这种动画效果是无法相比的，这些手段能提高学生的兴趣，加深学生对公式的理解，达到事半功倍的效果。

公式的引入还有很多其它方法，本文不能一一罗列出来，教师在教学时要做到淡化形式，不管使用任何一种方法，目标要在最短时间把学生引入到学习中来，达到最优效果。

2 公式的推导和论证

在新的数学公式引入后，学生的学习兴趣被激发了，对公式的证明、推导有了一定的愿望。这时候，教师应引导学生思考，分析证明相应的思路，找到合理的方法，针对中专学校学生的实际特点，找出适合他们基础的途径，培养、发展他们一定的逻辑分析能力。在推导、论证的过程中，尽可能的发挥学生的主体能动作用，能让学生推导的话就让学生推导，并留意他们推导中出现的问题。遇到有些特别复杂的公式，老师可酌情分析，用告知的形式向学生讲清楚为什么要这样用就行了。根据中职数学的大纲要求，我们只是要求学生要学会一些数学思路，学生对公式、性质的推导过程是无法完整掌握的，只需要求学生对数学公式、性质有正确记忆和恰当运用即可。

3 公式的强调

数学公式成立是要在一定的条件下的，学生学习了数学公式后，经常会乱套用公式，所以在教学中要强调公式成立的条件。如不等式等号成立时当且仅当学生往往容易会产生错觉，以为使用公式时就带上等号。例如求的最小值，采用到的错误结果，就是没有注意到不能成立的，而成立的

4 公式的记忆方法

数学公式的记忆方法有很多，主要包括以下几种方法：理解记忆法，口决记忆法、图像记忆法等。

4.1 理解记忆法

现代教育学表明，理解是记忆的基础和前提，只有对知识点理解得深入、透彻，才能将数学公式记得牢固、记得深。所以，对公式的含义、结构、使用范围、用法等各方面深入理解以达到增加记忆的目的。如组合数的公式的记忆为例，可借助生活的实例去理解两个组合数相等的情形，从中加深理解。例如从全班40名同学中抽出15人去开会，25名同学在课室里搞卫生，问有多少种挑选方法。这一问题很容易直接得到答案，也可以理解先挑25人即留在课室搞卫生，剩下的15人才去开会这么一种安排方法也是同等的安排方法。

4.2 表格记忆法

三角函数里公式很多，有些函数值可以用以下表格的特殊值来记忆，达到事半功倍的效果。第一行为正弦函数sinα的值，分母都是一样的，分子分别为接下来的余弦函数cosα的五个值，就是第一行的逆序排列。而第三行的正切函数tanα的函数值，可以引导学生从公式用第一行除以第二行，逐个计算出来。

4.3 图像记忆法

如同角三角函数关系式，有些公式比较难记忆，可采用图表来帮助记忆：

(2)阴影的三角形中，上面两个顶点的数值的平方各等于下面顶点的数值的平方，如

(3)六角形任一顶点的三角函数值等于相邻的两个顶点三角函数的乘职，如

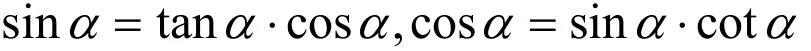
还有很多比较有效的记忆方法，如口诀记忆法，就是将数学公式的特征、规律总结为口诀，达到增强记忆的目的。如三角函数的多组诱导公式中，将它们总结为口诀“奇变偶不变，符号看象限”，这样把学生从复杂的几十个诱导公式的繁重压力中解放了。不管使用什么记忆方法，都要以理解掌握、灵活使用为目的，在记忆时应融洽贯通，切不可在某种方法上生搬硬套，死记硬背。

5 公式的应用

中职数学的教学的目的在于应用，如何能让学生灵活运用公式，这是一个很头痛的问题。很多教师在进行数学公式的教学时,常常会发现一个现象，“一讲就会，一做就错”，上课时老师已很详细地讲解了公式,又补充相应的例题，可是一到学生做练习时，一到运用公式做题就错呢?即便教师一直在提醒要注意的地方,学生还是会反复地做错呢?由于解题时需要综合运用多个公式、法则等知识，需要有较强的分析能力。

5.1 数学解题能力不会自然形成的，要教会学生从题目中寻求已知与结论的关系，理清解题思路，选择恰当的解题方法，切勿一拿到题目未经任何思考就瞎动笔或一味地单纯背题型。例如有一道题：在△ABC 中，已知求C边的长。如果采用正弦定理来解题的话，要分为两步，而且∠A有两种可能，而直接选择余弦定理就一步到位，不必分开情况来讨论了。

5.2 公式所反映出来的数学对象的关系是固定的，但应用公式时要注意公式形式的灵活，根据实际情况将公式正向运用、反向运用、变形运用等。授课老师应加强这方面的训练，可培养学生的灵活运用公式的能力。如在对数的运算过程中，对于根据题型需要，就可以产生很多变化形式。

5.3 数学公式教学应符合人的认知规律：实践、认识、再实践、再认识。对事物的认识是螺旋式的上升规律，在新知识的学习中不断充实，以达到加深理解、巩固记忆的目的。

中职数学公式的教学过程是千变万化的，必须以适当的方式将公式产生过程展示给学生，让学生通过自主学习获取相应的数学知识，能领悟公式、定理所包含的数学方法，灵活运用，从而达到提高分析问题、解决实际问题的能力。

[1]王颖秋.谈中职数学知识记忆的引导教学[J].科技信息,2011,(24).

[2]丁益民.关于数学公式教学的几点思考[J].中学数学》2011,(1).

[3]李卫国.数学公式演变对现代数学教学的启示[J].数学学习与研究,2009,(4).