基于K-空间积分格林函数的近场声全息技术
2012-09-01邵光辉牛悦娇马佳男
邵光辉,牛悦娇,马佳男
(1.中船重工第715研究所第十研究室,浙江 杭州 310012;2.河北联合大学,河北 唐山 063009;3.哈尔滨工程大学,黑龙江 哈尔滨 150001)
基于K-空间积分格林函数的近场声全息技术
邵光辉1,牛悦娇2,马佳男3
(1.中船重工第715研究所第十研究室,浙江 杭州 310012;2.河北联合大学,河北 唐山 063009;3.哈尔滨工程大学,黑龙江 哈尔滨 150001)
目前基于Neumann边界条件空间声场变换技术格林函数的主要有限离散化算法是k-空间抽样格林函数法.然而,该条件下的k-空间积分格林函数法却很少应用在相关的课题研究中.所以对于该算法的重构特性以及这两种算法在空间声场变换中的优劣是人们一直普遍关注的问题.本文通过计算修正了该算法在Neumann边界条件下的计算参数,并通过数值仿真分析了k-空间积分格林函数的相关特性,最后通过仿真计算给出了这两种方法在不同重构参数下的误差分析.这些分析结果可为进一步的工程实践提供参考.
空间声场变换;平面近场声全息;格林函数;法向质点振速
近年来,近场声全息技术得到了广泛的应用和发展,其中以基于空间声场变换(STSF)[1]~[3]、边界元(BEM)和最小二乘法这三种算法最为主流.目前这三种方法以基于空间Fourier变换和逆变换方法的NAH技术最为成熟,工程实现最容易,应用最广泛;BEM法和HELS方法虽然能适应各种形状的声源,却都有其自身缺陷,且工程实现存在不同程度困难.随着矢量水听器的发展,可以通过测量质点振速来对声场进行重建和预测,但现有的重建算法大部分都采用了K-空间抽样格林函数法对声场进行重建的,但是由于Neumann边界条件下k-空间振速-声压格林函数在辐射圆周上存在奇异性[4],这种奇异性会使得格林函数的幅值在辐射圆周上具有很大的跃变,从而影响重构精度.
本文将给出基于Neumann边界条件下的另一种格林函数重建算法--K-空间积分格林函数法,对声场进行重建,通过仿真计算验证这种格林函数离散方法的正确性和可行性,并用这种方法与K-空间抽样格林函数法进行比较,并给出相应的结论.
1 Neumann边界条件下的格林函数
理想流体介质中小振幅声波传播的波动方程[5]:

对于单频声波速度势Φ=覬e-jωt,ω为声波的角频率,覬是空间分布函数,它满足Helmholtz方程:

其中,c为声速,k为声波波数,故波数空间又称为k-空间.通过Helmholtz方程,可以推导出Helmholtz公式.此公式用声场边界函数值表示声场(稳态单频波动声场)的积分形式解.当点源都集中在某一封闭曲面s内时,Helmholtz公式表示为

由式(3)可见,Helmholtz公式用覬和鄣覬/鄣n边界值的面积分来确定声场中任意一点的速度势函数值,因此当已知边界质点振速的分布和声压的分布值时,就可以用Helmholtz积分求出场中任意点的速度势函数值.
格林函数表示一定边界条件下点源的场,与边界条件一一对应.单频声场中的格林函数满足下面的方程[6]:

其中,r軆'代表声源的位置,r軆代表场点的位置,δ函数表示点源,时间因子取e-jωt,解得:

式(5)表示的是自由场中的格林函数,称为格林函数的基本解.该式为具有1/r奇点形式的函数且满足Helmholtz方程,可以成为式(3)的辅助函数.利用格林函数这种可选性可以选择适当的格林函数形式来简化Helmholtz公式.
Helmholtz方程与第二类边界条件构成的定解问题叫做第二边值问题或Neumann问题.对于式(2),第二类边界条件是指鄣覬/鄣n在区域边界上为给定函数.相应地,该边界条件下满足式(5)和Neumann边界条件的解称为Neumann格林函数.
根据“虚源法”,平面边界下格林函数的数学表达式为:

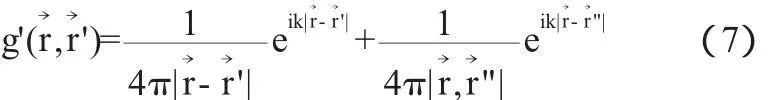
式(3)中,封闭曲面s外一点的速度势可以看作为s上次级元波在场点o的速度势迭加之总和,相当于源点位于s上.当s为平面时,有由式(7)可算出Helmholtz公式中的辅助函数项:


其中uz(x,y,z),p(x,y,z)分别为空间点(x,y,z)处为法向质点振速、声压.
通过式(8)可以得到Neumann边界条件下,实空间域下法向质点振速-声压的格林函数:

gN即为Neumann格林函数.由尤拉公式:
对式(3)进行二维空间Fourier变换并利用尤拉公式,整理得到k-空间法向质点振速-声压的格林函数:

2 K-空间积分格林函数法
K-空间积分格林函数法是由W.A.Veronesi等人提出的,哈尔滨工程大学的金莉萍修正了该格林函数法在辐射圆周上计算公式,本文将通过仿真计算分析该格林函数对重建结果的影响,并通过对双点源的仿真进一步验证该方法对重建分辨率和重建精度的影响.
由式(2)可以看出在基于Neumann边界条件下的格林函数在辐射圆周上具有奇异性,这种奇异性会使得格林函数的幅值在辐射圆周上具有很大的跳变,从而影响到重建的精度.K-空间积分格林函数法是通过格林函数在K-空间的积分值来改善函数在辐射圆周上的奇异性.其原理图如图1所示.

图1 K-空间积分原理图
在波数域的点(kx,ky)附近的环形区域带k2r2≤k2r≤k2r1上进行积分求格林函数G的平均值,以克服辐射圆周上的奇异性.记kr=(kx2+ky2)1/2,积分环带内径 kr1=(kx2+ky2)1/2-△kr,外径kr2=(kx2+ky2)1/2+△kr,其中,为环带宽度的一半.积分分为三个部分,即积分在辐射圆内小于kr2的传播波区域、倏逝波区域即大于kr2的区域,以及传播波和倏逝波混合的区域.
于是通过计算可得,在Neumann边界条件下的K-空间积分格林函数:

3 数值仿真分析
图2给出的是当重建距离增大时,K-空间积分格林函数的幅值随kr/k变化曲线.我们知道源面上的声波向全息面传播过程中,低波数的传播波成分幅值不发生变化;而高波数的倏逝波成分幅度将会按指数规律衰减.所以通过图2我们可以看到不同波数成分对格林函数的影响.

图2 距离不同时|GN|与kr/k间的关系
通过对比可以看出:(1)基于K-空间积分格林函数法的格林函数对重建距离更敏感,相较而言K-空间抽样格林函数对重建距离并不敏感;(2)当kr/k>1时(即高波数成分),K-空间抽样格林函数的幅值衰减迅速在kr/k=1.5时,幅值已衰减殆尽,而基于K-空间积分的格林函数幅值衰减速度远低于K-空间抽样格林函数,重建距离越小,该函数衰减速度越慢;(3)当kr/k=1时(即辐射圆周),可以看到两种格林函数都有幅值上的跃变,但K-空间积分格林函数在圆周上的幅值明显远小于K-空间抽样格林函数,说明K-空间积分格林函数法明显改善了式(2)在辐射圆周上的奇异性;(3)通过对两种格林函数衰减速度的对比,我们可以知道K-空间积分格林函数由于其衰减特性可以获得更多的高空间波数成分,尤其当重建距离较小时,可能会得到更好的重建精度.


图3 频率不同时|GN|与kr/k间的关系


图4 不同测量距离下,两种格林函数法的声场重建
由图3可以看出不同频率对格林函数衰减特性的影响,随着频率的减小,K-空间积分格林函数可以得到更多的高空间波数成分,而由于K-空间抽样格林函数倏逝波衰减的十分迅速,使得在低频条件下,很难捕捉到更多的高空间成分,这样会对重建精度产生相应的影响;随着频率的增大,两种格林函数在衰减特性上都没有明显的变化.
下面通过仿真验证,来进一步了解K-空间积分格林函数法对声场重建精度的影响.
首先,令全息面为4m×4m,重构频率f=1500hz,两个点源相距0.2m,采样点数N=64,声速c=1500m/s,dz=0.01m对声场进行振速-声压的声场逆向重构.
图4给出了在相同重构距离下,不同测量距离对声场重建精度和分辨率的影响.当测量距离Zh=0.02时,两种格林函数算法下的声场重建都获得了较好的重建分辨率,但是在基于k-空间抽样格林数算法下重建的声压在孔径边缘存在较小的起伏,这是由于“卷绕误差”和其格林函数本身存在奇异性引起的.将Zh增大到0.06m并保持重构距离dz不变,可以看到:随着测量距离的增大,两种格林函数下的重建分辨率都存在减小的现象,但是基于k-空间积分格林函数算法的重建结果仍然可以看出辐射声源的特性;但是随着Zh的增大,基于k-空间抽样格林函数算法下的重建声压幅值在孔径边缘的起伏增大,即使利用汉宁窗和k域滤波,都不能抑制卷绕误差对重构结果的影响,从而影响对声源特性的判断.
4 结论
通过数值仿真结果可以得出如下结论:当通过测量法向质点振速对声压场进行重构时,相对于k-空间抽样法,k-积分格林函数法有效地抑制了重构中常存在的“卷绕误差”并改善了k-空间抽样格林函数在辐射圆周的奇异性.当增大测量距离保持重构距离不变时,基于k-空间积分格林函数法相对于k-空间抽样格林函数算法的声场重建,具有相对较好的重构精度和重建分辨率,可以预见该算法在复杂声源存在的声场条件下会有较好的应用前景,其应用特点也可为进一步的工程实践提供参考.
〔1〕J.D. Maynard, E.G. Williams, Y.Lee, Near field Acoustic Holography: I. Theory of Generalized Holography and the Development of NAH,J.Acoust. Soc.m.1985,78(4):1395-1413.
〔2〕陈晓东.近场平面声全息的测量和重构误差研究[D].合肥工业大学,2004
〔3〕VeronesiW A,Maynard JD.Nearfield acoustic holography (NAH)II. Holographic reconstruction algorithms and computer implementation,J.Acoust.Soc. Am.1987,81(5):1307-1322.
〔4〕金莉萍.基于格林函数的典型声场反演技术[D].哈尔滨工程大学,2006.
〔5〕何祚镛.声学逆问题一声全息变换技术及源特性判别[J].物理学进展,1996(3).
〔6〕W.A.Veronesi and J.D.Maynard.Digital holographic reconstruction of source with arbitrarily shaped surfaces. J.Acoust.Soc.Am.,1989,85(2):588~598.
O438.1
A
1673-260X(2012)05-0008-04
