浅谈概率论教学改革

吴芙蓉

（呼和浩特民族学院，内蒙古 呼和浩特 010051）

浅谈概率论教学改革

吴芙蓉

（呼和浩特民族学院，内蒙古 呼和浩特 010051）

概率论是对随机现象的统计规律进行演绎和归纳的科学，是一门将数学的抽象内容与实际生活中的问题联系起来的课程，但目前高等院校概率论的教学普遍存在课程内容抽象难懂、教学方式单一死板、授课过程枯燥乏味学生缺乏学习兴趣等问题.本文针对概率论理论性强、应用广泛、内容抽象的特点，从教学内容、教学模式、考试考核等三个方面简单论述概率论教学改革.

概率论；教学改革

概率论是对随机现象的统计规律进行演绎和归纳的科学，是一门将数学的抽象内容与实际生活中的问题联系起来的课程，是我国高等院校教育中的三大基础数学课之一.它不仅广泛的应用于自然科学的各个领域，而且在社会科学的许多领域也日益受到重视.但因为概率论的课程内容抽象难懂、教学方式单一死板、授课过程枯燥乏味学生缺乏学习兴趣，因此对概率论教学进行改革是非常重要的.下面从三个方面简单介绍.

1 改革教学观念、教学内容

教学内容的改革是概率论教学改革的重要一部分.概率论的教学中普遍存在课程内容抽象难懂的问题，教授知识首先要让学生了解本课程，提起对本课程的学习兴趣，再让学生理解和掌握课程内容，并能应用所学知识.因此改革教学内容，要让课程教学内容趣味化、实用化.

在现实世界中发生的现象千姿百态，概括起来无非是两类现象：确定性的和随机性的.有一类现象，在一定的条件下是必然会发生的（或必然不会发生），例如，水在标准大气压下温度持续达到100℃时必然沸腾，温度为0℃以下时必然结冰；同性电荷相互排斥，异性电荷相互吸引等等，这类现象称为确定性现象.另有一类现象，在一定条件下，试验有多种可能的结果，但事先又不能预测是哪一种结果，例如，抛掷一枚硬币，可能正面朝上，也有可能反面朝上；买彩票有可能中奖，也有可能不中奖等等，此类现象称为随机现象，它们是不确定的.人们经过长期实践并经过深入研究之后，发现这类现象虽然就每次试验（或观察结果）来说，它具有不确定性，但在大量重复试验或观察下，它的结果却出现出某种规律性.概率论就是研究随机现象的规律性的一门数学学科.讲授教学内容时举一些同学耳熟能知的例子，使同学们能了解概率论所要解决的实际问题，引发同学们的学习兴趣.尽管如此，概率论的抽象性理论理解起来还是很难.要使学生们较快的理解概率论的理论，在教学内容上就要进行改革.对于一些抽象的基本概念注重选择生活、生产实践中的一些事例，运用数学的方法观察和分析这些实例，从而拉近概率论理论知识与实际生活的距离，并能触发学生听课的兴趣，促使学生对数学知识产生兴趣，更能加强数学理论知识的实用性与应用性.例如，概率论中的数学期望是一个比较抽象的数学概念.为了使同学们理解这个概念，从生活中的平均数推出加权平均数，很自然的定义出数学期望的概念.它就是按概率取平均.例如：

要评判一个射手的射击水平，需要知道射手平均命中环数.设射手A在同样条件下进行射击，命中的环数X是随机变量，其分布律如（表1）所示.

表1

由X的分布律可知，若射手A共射击N次，在N次射击中，大约有0.1×N次击中10环，0.1×N次击中9环，0.2×N次击中8环，0.3×N次击中7环，0.1×N次击中6环，0.1×N次击中5环，0.1×N次脱靶.于是在N次射击中，射手A击中的环数之和为

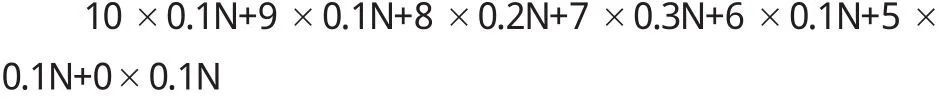
平均每次击中的环数约为

在概率论中这种与生活、生产实践有密切联系的实际例题很多，通过讲解这些例题，不仅能提高学生的学习兴趣，更能使理论教学内容生动，简单易懂，还能加强教学内容的实用性与应用性.

2 改革课堂教学模式、教学方法

概率论教学改革的第二部分是改革教学模式.教学模式是指教学思想和教育理论指导下形成教学活动的基本框架.教学方法是为了达到教育目的、完成教学任务所采取的教学方式和手段的一套完整体系.传统的教学模式、教学方式单一死板、授课过程枯燥乏味使学生缺乏学习兴趣，教学内容更加难懂、难用.因此对教学模式、教学方法进行改革是非常有必要的.

首先在课堂教学中运用多媒体教学.多媒体具有丰富的表现力，能将文字、图表、声音和动、静图像集成在一起，构成教学软件，创造一个图文并茂、有声有色、生动逼真的教学环境，使内容更充实、更丰富、更形象、更具吸引力，从而提高了学生的学习兴趣，增强了教学内容的趣味性.概率论是研究随机现象统计规律性的一门学科，而要想获得随机现象的统计规律性，就要进行大量重复试验，其教学过程中，大多数概念及例题背景知识较多，书写耗时费力，这在有限的课堂时间内难以实现.为此，我们在教学中采用多媒体辅助手段，通过计算机图形演示、动画模拟、数值计算及文字说明等，增加课堂教学信息量，提高学习效率，达到教学目的.

其次课堂教学直观化，就是在对知识点给予严密陈述和严谨推理的同时，尽量让学生获得直观性的印象，了解它们的直观意义，以便于学生理解、掌握和记忆.在教学中，教师可以采用图形的形式，表达概率论问题的实质与思路，是学生借助视觉迅速感知并理解，从而使抽象变得具体，启发学生的思路.例如，讲授事件的运算时，可通过集合图形加以说明时间运算的定义，能使学生更简单直观的理解和掌握新知识；又例如，讲授分布函数求法时，可通过图形来说明其定义，能让抽象的分布函数定义变得具体、简单、直观、深刻.可以举一个例子：

随机变量X的分布律如（表2），求其分布函数F(x).

表2

由随机变量X的取值可知，可将x轴分为五个部分，分布函数F(x)=P{X≤x}是随机变量X小于等于数x的概率，因此，

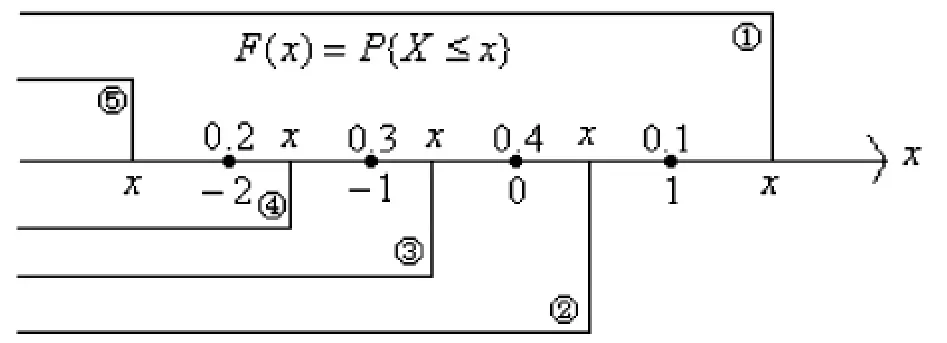
图1

（1）x≥1时，由（图1）中①可知,随机变量X的所有取值都包含在事件X≤x当中，故F(x)={X≤x}=1；

（2）1>x≥0时，由（图1）中②可知,随机变量X的三个取值包含在事件X≤x当中，故F(x)={X≤x}=0. 2+0.3+0.4=0.9；

（3）0>x≥-1时，由（图1）中③可知,随机变量X的两个取值包含在事件X≤x当中，故F(x)={X≤x}=0.5；

（4）-1>x≥-2时，由（图1）中④可知,随机变量X的一个取值包含在事件X≤x当中，故F(x)={X≤x}=0.2；

（5）-2>x时，由（图1）中⑤可知,随机变量X的所有取值都不包含在事件X≤x当中，故F(x)={X≤x}=0.

即，随机变量X的分布函数为

如此，通过图像，分布函数这个抽象，难懂的内容变得具体、简单、直观、深刻.同样在课堂教学中，对于一些抽象的公式，教师在严格证明的同时，运用示意图方法、直观理解方法讲述其直观的理解，让抽象难懂的课程内容变得具体、简单，印象直观、深刻.这会有助于学生的理解、掌握和记忆.

3 改革课程考试考核方法

随着教学观念、教学内容、教学模式、教学方法的改革，对概率论考试考核方式进行改革也是十分有必要的.高等学校加强素质教育，要求我们必须把传授知识、培养能力、提高素质三者有机结合.以往的考试考核形式是期末闭卷考试80%，平时成绩20%决定该门课程的成绩，这样的考核方法理论考试起主导作用，不能真实反映学生的实际能力，尤其对学生的应用能力没有进行考核.通过改革将本课程的考核方法修改为期末考试40%、期中考试20%、平时成绩40%.期末考试为闭卷考试，主要考核学生对本课程概念、性质、定理等理论知识的掌握情况；期中考试为开卷考试，主要考核学生的对教材的掌握及对理论知识的应用情况；平时成绩由课堂提问、解题，课后作业，小测试，试验，小论文等部分组成，主要考核学生的应用能力、分析能力、实践能力、自学能力、表达能力、理解能力等等.通过这样考试考核方法，不仅能对学生的理论知识的掌握进行考核，也能对学生的实际应用能力进行考核.

教学改革是一项长期而复杂的系统工程，不能一蹴而就.在现行的高等教育体系下，随着概率论的迅速发展和人才培养模式的转变，必须对课程教学进行改革，采用灵活多变的教学方法和形式，致力培养学生的综合素质能力是我们永远的目标.在今后的教育教学当中，将继续从多方面进行教学改革，达到培养综合素质能力的学生的目标.

〔1〕韩旭里，谢永钦.概率论与数理统计[M].复旦大学出版社，2011.

〔2〕齐淑芬.关于概率论课的教学改革[J].天津成人高等学校联合学报，2001（5）.

〔3〕郝香芝，田贵辰，赵永强，张东凯.《概率论与数理统计》教学改革研究[J].石家庄学院学报，2009（5）.

〔4〕李昌兴，正生.概率论与随机过程课程教学改革的研究与实践[J].西安邮电学院学报，2009（11）.

〔5〕陈忠伟，会殊荣，郑钰.高等学校概率论教学改革的探索与实践[J].沈阳农业大学学报，2011（5）.

〔6〕章山林.工科《概率论与数理统计》的教学改革[J].常熟理工学院学报，2008（12）.

G 642.0

A

1673-260 X（2012）10-0007-02