氧化锆氧传感器电压输出特性模型的研究

黄彩虹，金福江

（华侨大学 信息科学与工程学院，福建 厦门361021）

在工业生产的燃烧过程、氧化反应和生化处理等过程中，都需要利用氧化锆氧传感器作为测量元件，测量和控制混合气体中的氧体积分数。例如，通过对烟道气中氧体积分数的测定来控制锅炉燃烧过程，可以提高锅炉燃烧的热效率；又如在污水处理场的生化过程中，控制一定氧体积分数的混合气体，使某种微生物大量繁殖，以促进生化过程［1］；在汽车发动机中，氧传感器用于测定废气中的氧体积分数，控制程序根据该信号，修改喷油时间、点火时间等参数，以实现节油和减少环境污染。由此可见，氧传感器是一个重要的反馈元件，氧传感器输出信号的准确性将直接影响生产过程的工作效率、可靠性［2］。

氧化锆测氧利用固体电解质浓差电池的原理，由能斯特方程来表述氧电势与待测氧体积分数之间的关系。能斯特方程是一个理想公式，针对的是理想气体，然而，工业氧化锆测氧过程中存在现场噪声复杂、探头老化快、不同探头具有离散性等不利因素，直接使用能斯特公式进行测量，会给测量带来误差。目前国内的测氧仪表只对方程进行了微小的改动［3－5］，准确度较差。笔者根据现场实际测量到的氧体积分数与氧传感器两段电势的数据表，进行线性回归分析，提出了新的数学模型，可以有效地降低误差。

1 氧传感器测氧原理

1.1 氧化锆固体电解质导电机理

电解质溶液导电是靠离子导电，某些固体也具有离子导电的性质，称为固体电解质。凡是传导氧离子的固体电解质称为氧离子固体电解质。氧化锆也称二氧化锆（ZrO2），分子是由1个锆原子和2个氧原子结合而成。纯净的氧化锆基本上是不导电的，是不能进行氧体积分数测量的，在氧化锆中加入氧化钙（CaO）后，就具有高温导电性，这样就可以进行氧体积分数测量。

如在ZrO2中加入一定数量的CaO，Ca2＋在进入ZrO2晶体后会置换出Zr4＋，由于钙离子和锆离子的离子价不同，在晶体中会形成许多氧空穴。在高温（750℃以上）下，如有外加电场，就会形成氧离子占据空穴的定向运动而导电。带负电荷的氧离子占据空穴，也就相当于带正电荷的空穴做反向运动，也可以说固体电解质是靠空穴导电的，这和P型半导体靠空穴导电机理相似。固体电解质的导电性能与温度有关，温度越高，导电性能越强。

ZrO2测量含氧体积分数的基本原理是利用所谓的“氧浓差电势”，即在一块ZrO2两侧分别附以多孔的铂电极（又称“铂黑”），并使其处于高温下。如果两侧气体中的含氧体积分数不同，那么在两电极间就会出现电动势。此电动势是由于固体电解质两侧气体的氧体积分数不同而产生的，故叫氧浓差电势，这样的装置叫做氧浓差电池，原理如图1所示。

图1 氧浓差电池原理

氧浓差电池两侧分别为氧体积分数不同的两种气体。氧分子首先扩散到铂电极表面吸附层内，高温下在多孔铂电极中变成原子氧，然后扩散到固体电解质和电极界面上。由于固体电解质内有氧离子空穴，扩散来的氧原子便从周围捕获2个电子变成氧离子进入空穴，同时产生2个电子空穴。铂电极中自由电子体积分数高且逸出功小，所以产生的2个电子空穴立即从铂电极上夺取2个电子而达中和。当氧离子空穴被氧离子填充后，形成一个完整的晶格结构。由于在电极上和固体电解质界面上空穴中氧离子体积分数较高，在扩散作用下，进入氧离子空穴的氧离子还会跑出来，去填补靠近的氧离子空穴，空出来的位置又由新进入的氧离子所填补。这样直到氧离子到达另一电极，释放出2个电子成为氧原子，并与其他氧原子结合成为氧分子。应当指出，氧离子的这种扩散迁移是双向的，但由于氧浓差电池两侧气体的氧体积分数不同，氧分压不同，因而总的趋势是氧离子从氧体积分数高的一侧向体积分数低的一侧扩散，即氧从电极1上得到电子，通过氧离子空穴迁移到电极2后释放出电子，变为氧气。这时在电极1（阴极）产生下列反应：

到达电极2（阳极）后，将产生下列反应：

这样在电极上产生了电荷的积累，从而在两极板间建立了电场，此电场将阻止这种迁移的进一步进行，直至达到动态平衡状态，此时在两极板间形成电势。

1.2 氧传感器动态机理模型［6－7］

根据氧传感器测氧原理，氧浓差电势的大小可由能斯特（Nerenst）公式计算得出：

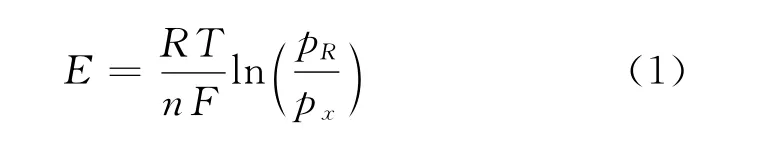
式中：E——氧浓差电势，mV；R——理想气体常数，R＝8.314J／（mol·K）；T——氧化锆管的绝对温度；n——1个氧分子输送的电子个数，n＝4；F——法拉第常数，F＝9.65×104C／mol；pR——参比气体氧分压；pX——被测气体氧分压。

在工业应用中，一般取参比气体为空气，pR＝20.95%，代入式（1），得到测量氧体积分数的计算公式，即式（2）。

当T一定，电池产生的氧浓差电势与被测气体的氧体积分数成单值函数关系。目前，氧化锆氧测氧仪表根据氧传感器输出的浓差电势E，得到被测气体的氧体积分数。有些设计，会考虑新锆头特性差异的补偿量，在此公式基础上加补偿量。

2 软测量模型的建模与分析

考虑到能斯特方程是一个理想公式，针对的是理想气体，其模型与实际环境不一定一致。笔者对氧传感器信号进行实测实验，采用国产ZrO2，φ9mm管（700℃）、配合氧体积分数连续可调的锆头检定仪，当氧电势为20～180mV时，得到表1数据。首先，对表1中的数据建立以氧电势为自变量，氧体积分数为因变量的数学模型。其次，利用MATLAB软件对已建立的数学模型的未知量进行求解，并对求解后的模型进行检验；最终利用逐步回归法对检验模型进行优化。

表1 氧电势与氧体积分数关系

初建线性回归模型：

根据试验数据，利用MATLAB统计工具箱中的命令regress进行求解［8］，得到方程：

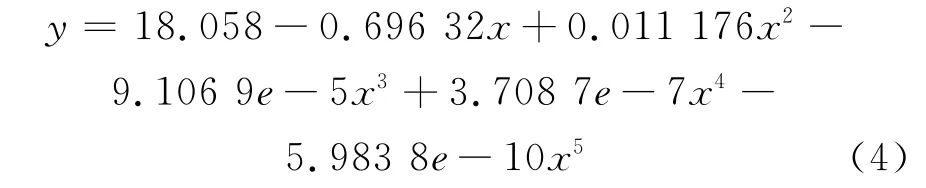
对该模型进行F检验［9］，得到相关系数R2＝0.999 81，统计量F＝783 91，概率P＝0.0000。通常，若R的绝对值在0.8～1，可推断回归变量之间具有较强的线性相关性。该模型的拟合优度R2的绝对值为0.999 81，表明回归变量之间线性相关性较强。当F＞F（1－α）（k，n－k－1）（其中，α——预定显著水平，本文取0.05；k——自变量个数；n——试验样本数，本文为80）时，认为因变量y与自变量x之间存在显著的线性相关关系；否则认为线性相关关系不显著。该模型的统计量F＝7.839 1＞F（1－0.05）（1，120）＝3.92，则说明y与x之间存在显著的线性相关关系。显著性概率P＝0.0000＜0.05，则进一步说明y与x之间存在显著的线性相关关系，因而模型（4）可以选用。

按照能斯特方程做出的理论曲线与实际曲线、回归分析曲线的对照如图2所示，可见，回归分析所得的曲线更接近于实际曲线。因此，在实际应用中，每次测得的电势值经过数字滤波、老化补偿后，代入式（3），即可得到氧气体积分数。

图2 各模型曲线比较

系统的残差如图3所示，不难看出，残差条均通过零线，说明它们不是异常值，但样本1.74，80为奇异点。如果进一步进行模型优化时，应剔除该数据。

图3 新模型的残差图

3 结束语

为了减少测量误差、探头老化、噪声干扰对氧化锆氧传感器测量精度的影响，本文建立一定温度下氧化锆氧传感器的氧电势与氧体积分数机理模型，用实际数据辨识模型参数，并验证了模型的有效性。该模型与传统应用的能特斯模型，误差值更小，更适用于氧化锆氧传感器控制系统的仿真及设计，可以明显提高氧化锆氧传感器的检测精度和稳定性。

［1］陈玉霞.氧化锆氧分析仪及其应用［J］.石油化工自动化，2008，44（04）：58－59.

［2］李忠友.氧传感器的结构原理与检测［J］.实用汽车技术，2008（03）：31－32.

［3］王孝良，赖晓晨.氧化锆测氧的数据处理方法［J］.现代科学仪器，2003（04）：58－59.

［4］路顺，林健，陈江翠.氧化锆氧传感器的研究进展［J］.仪表技术与传感器，2007（03）：1－3，6.

［5］罗志安，肖建中.氧化锆传感器电极电化学性能研究［J］.武汉科技大学学报，2008，31（04）：386－388.

［6］马博，梁楚华，周建.基于MATLAB的短电弧加工工艺模型回归分析与研究［J］.机械工程与自动化，2011（04）：45－47.

［7］钟丽颖，金福江.热定型工艺优化设计系统［D］.厦门：华侨大学，2010.

［8］钟丽莹，金福江.基于LS－SVM棉／氨纶弹力布热定形效率预测［J］.武汉理工大学学报（信息与管理工程版），2010，32（01）：88－91.

［9］盛骤，谢式千，潘承毅.概率论与数理统计［M］.北京：高等教育出版社，2005.