基于预期电压矢量的永磁同步电机直接转矩控制系统*
2012-08-28王少珠黄韬
王少珠, 黄韬
(1.重庆邮电大学计算机科学与技术学院,重庆 400065;
2.福州大学电气工程与自动化学院,福建福州 350108)
0 引言
直流电机很早就被人们广泛应用于生产和生活中。但是,由于电刷及换向器的限制,直流电机表现出调速范围窄、参数扰动鲁棒性差、维护费用高、过载能力弱等缺点,使其在性能要求较高的场合中的进一步推广受到极大限制。永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)具有高功率密度、高效率、高可靠性等优良的动态特性,而且过载能力强、转矩密度大,更加适用于电动汽车、混合动力汽车等各种性能要求高的场合,发展前景广阔[1]。
1985年,德国鲁尔大学的M.Depenbrock教授及日本的I.Takahashi教授先后针对异步电机提出了直接转矩控制理论[2-3],并于1987年将其推广至弱磁调速范围。直接转矩控制是一种高性能的交流变频调速技术,它通过检测电机定子电压和电流,借助瞬时空间矢量理论计算电机的磁链和转矩,并根据与给定值比较所得差值,实现磁链和转矩的直接转矩控制。此方法仅涉及到定子电阻和电感,对电机参数的依赖性较小。
传统的直接转矩控制系统一般是将定子磁链和转矩的偏差信号输入到两个滞环比较器,并根据滞环比较器的输出及定子磁链的空间相位经过查表选择合适的电压矢量。这种基于开关表的直接转矩控制构造出来的空间电压矢量数量有限,在空间是离散分布的,不能很好地满足每一个控制周期内对控制电压提出的要求;而且在扇区交界处,可能出现扇区的错误选择,从而造成电机的振荡现象[4]。针对该问题,本文对基于预期电压的直接转矩控制系统进行研究,并利用MATLAB进行了对比仿真试验,试验结果表明基于预期电压的直接转矩控制相对于传统的直接转矩控制在各个方面都具有更好的控制效果。
1 PMSM数学模型
1.1 直接转矩控制的提出
在表贴式PMSM(SPMSM)中,电机定子电感的dq轴分量Ld=Lq=L,不存在磁阻转矩,电机的电磁输出转矩为

式中:pn——电机极对数;|
ψ|s——定子磁链幅值;
ψf——转子磁链;
δsf——转矩角。
将定子磁链幅值控制为定值,对式(1)两端求 δsf的微分:

由式(2)可知,当 δsf在[-π/2,π/2]范围内变化时,电磁转矩Te与δsf的变化趋势是一致的,故可利用δsf来控制转矩Te。
综上,直接转矩控制可分为双闭环:一个闭环的控制目标是将磁链的幅值控制成一个不变的值,而另一个闭环实际上就是控制转矩角,使得磁链在空间内环绕成圆形。
1.2 PMSM的定子磁链与转矩
由上述可知,定子磁链与转矩是实现直接转矩控制系统必须的信息。根据SPMSM三相绕组的电压方程,可得其电压矢量方程[6]:

对式(3)进行移项操作,两边积分,并分解成αβ坐标轴下的分量,得定子磁链的估计算子:

得到定子磁链后,利用式(7)可得电磁转矩估计值:

2 SVPWM
SVPWM的理论基础是平均值等效原理,即在一个控制周期内通过对相邻两个基本电压矢量及零矢量作用时间加以控制,使其平均值与给定的电压矢量相等[6]。
如图1所示,非零电压矢量U1~U6将整个矢量平面分成6个60°的扇区,两个零矢量在平面的中心。图中,t1和t2分别是电压矢量U1和U2的作用时间,usref是预期电压矢量,uαref和uβref分别是usref的α轴和β轴分量,θuref为usref的空间相位角。按图1所示的方式可合成每个扇区内的任意电压矢量,即:

式中:Ux和Uy分别是两个相邻的基本电压矢量,U0和 U7分别是两个零矢量,tx、ty、t0、t7分别是它们的作用时间。
现假设预期电压矢量usref在第Ⅰ扇区,如图1所示,其相邻基本电压矢量为U1和U2,可用U1、U2、U0和U7合成该电压矢量。由正弦定理可得


得到每个基本矢量的作用时间后,讨论如何产生合理的PWM波。在SVPWM方案中,零矢量的选择是比较灵活的,适当的选择零矢量可最大限度地减少IGBT的开关次数,延长其寿命。因此,可将基本矢量作用顺序确定为每次开关状态转换时,只改变其中一相的开关状态,并对零矢量进行了平均分配,产生对称的 PWM波,降低PWM的谐波分量。为了输出对称的PWM波形,在不同扇区安排不同的开关顺序,各扇区的开关切换顺序如表1所示。

图1 基本电压矢量分布图

表1 开关切换顺序表
同样以第Ⅰ扇区为例,在控制周期Ts内,其三相PWM波形如图2所示。其中A、B、C分别为A、B、C相绕组所连接的逆变器上桥臂的IGBT控制端。
3 基于预期电压矢量的直接转矩控制
针对传统的基于开关表的直接转矩控制空间电压矢量数量有限,不能很好地满足每一个控制周期内对控制电压提出的要求,在扇区交界处,可能出现扇区的错误选择等现象。考虑SVPWM能够合成空间内一定幅值范围内的任何相位的电压矢量,可采用SVPWM替代开关表与滞环比较器的传统方法产生电压矢量。

图2 扇区Ⅰ的三相PWM波
采用SVPWM的方法产生电压矢量,需要有一个期望的电压矢量作为输入,该电压矢量可称之为预期电压矢量。
3.1 预期电压矢量的确定
对于SPMSM,由式(1)取微分得

在直接转矩控制中,定子磁链幅值 | ψ|s被控制成恒值,可忽略其对转矩变化的影响,故转矩的增量ΔTe决定于转矩角增量Δδsf。
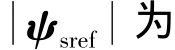

图3 转矩角增量
又,在αβ坐标系中,PMSM电压矢量方程为

由图3及其分析,可将式(12)近似表示为

式中:Ts——控制周期;
uαref、uβref——分别为预期电压矢量的 α 轴和β轴分量。
3.2 基于预期电压的直接转矩控制系统
由上述预期电压矢量的计算方法可知,欲获得预期电压矢量必须有期望的定子磁链矢量作为输入。定子磁链的期望幅值较易获取,根据图3可知,定子磁链的期望空间相位可由当前定子磁链的空间相位加上转矩角增量获得。
由式(12)可利用一个PI控制器将转矩的偏差信号调理成转矩角的增量信号。增量信号与当前定子磁链的空间相位相加,输入到预期电压矢量计算模块。基于预期电压的直接转矩控制框图如图4所示。

图4 基于预期电压的直接转矩控制框图
4 仿真试验及结果分析
为了证明基于预期电压的直接转矩控制策略相对于传统直接转矩控制策略的优势,利用MATLAB/Simulink分别对两种控制策略进行仿真试验。同时,SPMSM(Ld=Lq)作为控制对象。其具体技术参数如表2所示。

表2 电机技术参数表
设采样周期为10-6s,速度PI控制器的最大输出电磁转矩为6 N·m,最小为-6 N·m,参考转速为800 r/min,定子磁链控制在0.2 Wb,负载转矩设置为2.5 N·m,分别按照上述基于预期电压的直接转矩控制策略构造Simulink模型。并与传统的基于开关表的直接转矩控制策略作比较,为了保证下面对比试验的说服力,模型中速度环PI控制器的Kp经调节后,应与传统直接转矩控制模型的PI控制器相等,Ki亦同。
设置运行时间为0.18 s,分别运行两个Simulink模型,得到图5所示的电机三相电流波形。

取A相电流0.073 2 s后的4个周期波形,进行FFT分析,结果如图6所示。

图5 PMSM三相电流波形仿真图

图6 A相电流的FFT分析
从图6可看出,相对于预期电压的直接转矩控制,基于开关表的直接转矩控制的A相电流存在着38~50 kHz之间的高次谐波,波形畸变率较高。可见预期电压的直接转矩控制能够较好地控制PMSM的定子电流。分别画出两种控制策略产生的磁链圆,如图7所示。由图7可看出两种控制策略都能够很好地控制磁链,说明直接转矩控制能够很好地控制磁链幅值。
计算可得,基于预期电压的直接转矩控制产生的磁链幅值方差为0.067,而基于开关表的直接转矩控制产生的磁链幅值方差为0.026 6。故,相对而言,基于预期电压的直接转矩控制产生的磁链波动较小。

图7 磁链圆
因系统在0.007 s处已基本达到稳定状态,故选择0~0.03 s的转矩及转速数据进行比较,如图8、图9所示。
由图8可知,两种控制策略同样能够很好地控制PMSM的电磁输出转矩。
为了比较两种控制策略在控制转矩方面的优劣性,与磁链幅值的比较相同,分别计算两种控制策略得出的转矩响应方差,取0.02~0.03 s的转矩响应数据计算转矩的稳态方差:
基于预期电压的转矩响应稳态方差=1.489 3
基于开关表的转矩响应稳态方差=3.084 1
由上述方差可看出,基于预期电压的直接转矩控制产生的转矩响应具有更小的转矩脉动。
由图9(a)可知,基于预期电压的直接转矩控制的速度响应具有更短的上升/调节时间,这是由于基于预期电压的直接转矩控制的转矩动态响应压矢量,为了改善直接转矩控制的控制性能,本文对基于预期电压矢量的SVPWM直接转矩控制进行研究,并与传统的直接转矩控制进行了仿真对比试验。试验结果表明,基于本文所提出的直接转矩控制策略无论在定子电流、磁链幅值、转矩响应还是速度响应的控制都优于传统基于开关表的直接转矩控制。幅度较大。将图9(a)局部放大得到图9(b)。
由图9(b)可知,基于预期电压的直接转矩控制速度响应具有较小的稳态误差。

图8 转矩响应曲线
5 结语
由于SVPWM能够产生空间内任意相位的电

图9 两种控制策略的速度响应曲线
[1]王成元,夏加宽,孙宜标,等.现代电机控制技术[M].北京:机械工业出版社,2009.
[2]DEPENBROCK M.Direct self-control(DSC)of inverter-fed induction machine[J].IEEE transactions on industrial electronics,1988,3(4):420-429.
[3]TAKAHASHI I,NOGUCHI T.A new quick-response and high efficiency control strategy of an induction motor[J].IEEE Transaction on Industry App,1986,22(5):820-827.
[4]LIU L,ZHOU W,RONG X.Research on direct torque control of permanent magnet synchronous motor based on optimized state selector[J].IEEE International Symposium on Industrial Elec,2006,3(2):2105-2109.
[5]李耀华,刘卫国.永磁同步电机直接转矩控制不合理转矩脉动[J].电机与控制学报,2007,11(2):148-152.
[6]周扬忠,胡育文.交流电动机直接转矩控制[M].北京:机械工业出版社,2011.
[7]陈振,刘向东,戴亚平,等.采用预期电压矢量调制的PMSM直接转矩控制[J].电机与控制学报,2009,13(1):40-46.
