无速度传感器在矿用电机车矢量控制系统中的应用

2012-08-28陈名辉徐立波

电机与控制应用 2012年2期

陈名辉，阮毅，宗剑，徐立波，柳巍

(1．上海大学机电工程与自动化学院，上海 200072;2．上海应用技术学院，上海 201418)

0 引言

直流电机体积大、维护困难、运行成本高、电刷易产生电火花，不利于防爆。牵引电机中，异步电机已逐步代替直流电机，成为主要的轨道牵引用电机。选择矢量控制作为控制方法可获得较好的交流调速性能。

矿用电机车通常工作在比较恶劣的环境中［1-2］。供电系统稳定性差;轨道高低不平，机车需要频繁起动、制动、加速、减速，并要适应上、下坡和颠簸路况，震动强烈;电磁干扰严重。因此，为获得较好的控制性能，应针对实际的工况要求对传统的矢量控制系统进行改进。速度传感器存在测速精度受安装精确度影响、维护困难以及受工作环境影响等问题，故采用无速度传感器。

无速度传感器矢量控制需要准确估算转速和磁链信息。传统的电压模型在低速时，由于定子电阻压降作用明显，测量误差淹没了反电动势，使得观测精度较低。传统的电流模型由于电机运行导致转子温度上升或磁路饱和，转子时间常数变化较大，影响其磁链观测精度，高速时不适用。因此，仅采用电压模型或电流模型难以满足宽速度范围的转速估算精度要求。为解决此问题，模型参考自适应法提供了一个很好的思路。

本文首先对系统中的基于模型参考自适应(Model Reference Adaptive System，MRAS)转速估算环节进行分析研究，然后采用改进型电压模型对系统进行改进，在此基础上搭建了一套基于MATLAB/Simulink的电机控制仿真系统，进行了MRAS转速估算的仿真。仿真结果表明该方法能够准确估算转子磁链与转子转速，系统运行良好。

1 基于MRAS的转速估算方法

1．1MRAS 原理

MRAS的主要思想是将不含未知参数的方程作为参考模型，将含有待辨识参数的方程作为可调模型，利用两个模型具有相同物理意义的输出量的误差构成合适的自适应律，来实时调节可调模型待辨识的参数，最终达到控制对象的输出跟随参考模型的目的。MRAS是一种基于稳定性设计的参数辨识方法，通过选取合适的自适应律，可保证参数辨识的渐进收敛［3］。

1．2 参考模型的选择

MRAS采用两种结构不同，输入变量也不同的模型，其中以不包含待辨识电机转速的模型作为参考模型，以包含待辨识电机转速的模型作为可调模型。

电压模型方程为式中:ψrα，ψrβ——分别为两相转子磁链，其中下

标u表示电压模型;

Lr——转子电感;

Lm——互感;

usα，usβ——分别为两相定子电压;isα，isβ——分别为两相定子电流;Rs——定子电阻;

Ls——定子电感;

1．3 可调模型的选择

电流模型方程为

式中:下标i——电流模型;

p——微分算子;

Tr——转子时间常数，Tr=Lr/Rr;

电流模型中含有转速项，所以选择电流模型作为可调模型。

1．4 自适应律

电压模型和电流模型的输出都是转子磁链的两个分量ψrα和 ψrβ。选择合适的自适应律，可以提高系统稳定性和估算转速精度。

根据Popov超稳定理论，按MRAS参数的结构，速度估算子模块将估算转速取为比例积分形式。自适应律为

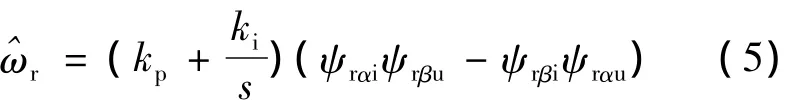
MRAS系统结构如图1所示。

图1 MRAS系统结构

2 改进型电压模型

从式(1)、式(2)可看出，电压模型中存在纯积分环节，实际计算中，存在两个问题:第一是积分初值问题，因为只有ψr从零相位开始积分才能使输出值正确，否则一直包含一个初始直流分量;第二是直流漂移导致积分溢出，实际应用中因为传感器误差引起的电压电流检测偏差，直流偏置及积分漂移现象，在长时间积分后导致纯积分环节的溢出，使得估算磁链不准，造成矢量控制的性能变差。

为克服上述问题，采用增加一个高通滤波器环节以消除影响。估算环节传递函数为

式中:x——系统输入;

y——系统输出;

ωc——截止频率。

由传递函数可知，纯积分与一阶高通滤波器的组合可等效为一阶惯性环节。

由于一阶惯性环节的引入会使得磁链幅值衰减并使相位滞后。当运行频率等于一阶惯性环节的截止频率时，磁链观测幅值约为实际的1/，相位滞后实际值π/4，如果不进行有效补偿，将导致磁场定向位置不准确，使得矢量控制解耦不完全，所以需要进行有效补偿。转子磁链补偿参考值可使用电流模型的磁链输出值［4］，也可使用电压模型输出经过饱和限幅后的值作为磁链参考补偿［5］，本系统中采用的改进型的电压模型如图2所示。

图2 改进型电压模型结构框图

该方法是通过引入定子电流d轴分量，与互感Lm相乘，得到参考值ψ*r，通过低通滤波器补偿磁链幅值与相位。该方法更简单，易于实现，有较好的效果。由式(7)可知，假设磁链初始值ψr=，则误差为零;当初始值 ψr≠ψ*r，存在积分漂移时，改进型的电压模型开始引起ψ^动态收

r敛，收敛速度取决于滤波时间常数Tr。由于受电流、温度、频率等变化引起的电阻变化导致的估算误差，可通过选择适当的Tr来加以削弱，能有效抑制积分漂移，得到比较准确的ψr。

3 无速度传感器矢量控制系统的设计

无速度传感器矢量控制系统的结构如图3所示，由坐标变换模块、MRAS模块、PI调节器和SVPWM模块等组成。通过检测的电子电压、电流经过3s/2s变换得到αβ坐标系下的定子电压usα、usβ和电流isα、isβ，将这些量输入到 MRAS 转速估算模块与改进型电压模型磁链观测模块得到转速估算值^ωr与磁链角φ，分别反馈到转速比较环节，以及用于逆旋转变换的磁链角定向。

图3 无速度传感器矢量控制系统框图

4 仿真结果及分析

为验证上述速度估算法的正确性及方案的可行性，在MATLAB/Simulink下建立了无传感器矢量控制仿真系统，并进行仿真。仿真中采用的异步电机的额定参数如下:PN=4 kW、fN=50 Hz、np=2、UN=400 V、Rs=1.405 Ω、Rr=1.395 Ω、Lm=0.245 H、Ls=Lr=0.012 H、J=0.013 1 kg·m2。

仿真过程中采用定步长的接法求解，仿真算法 ode32tb。仿真时空载起动，在系统运行到t=0.2 s时，突加一个阶跃负载转矩，大小为10 N·m。仿真结果如图4、图5所示。