基于RVACD和WPE感应电机转子断条故障诊断

刘 进， 王 莉， 吴家梁

(空军工程大学防空反导学院，陕西三原 703800)

0 引言

转子断条故障是感应电机常见的故障之一，占电机总故障的10%［1］。感应电机在起动时，转子会承受很大的冲击力，电机反复起动，会导致转子导条和端环变形。由于各部分位移量不同，受力不均匀，加上导条的生产质量存在问题，导致导条受应力分布不均而断裂。转子故障严重时会因转子扫堂擦伤定子铁心，导致整机报废［2］。因此研究转子断条故障的诊断方法十分必要。

目前对转子断条故障诊断主要是分析定子电流，但是存在诸多不足之处:例如利用起动电流作时变频谱分析时，起动时间短，采样困难［1］;Fourier变换处理转子断条故障信号效果较差。有人提出对电机的断电残压进行分析，该方法在断电的情况下可避免外界因素的影响;Shannon熵具有较强的容错能力，小波包分析很适用于处理复杂非平稳信号。因此，本文提出利用小波包熵分析断电残压的方法进行转子故障诊断。

1 转子断条故障在断电残压中的表现

感应电机工作时定子三相电流在气隙中形成旋转磁场F1，磁场切割定子绕组产生感应电动势E1，在定子回路中的单相电压方程为——;

式中 相电压

磁场F1也切割转子，在转子回路上产生感应电动势和电流。设转子电流产生的磁场为F2，F1和F2共同作用则形成感应电机的气隙合成磁场F。正常工作中的电机突然断电后，定子电流I1突降为0，导致磁场F1消失，但是定、转子间的磁通不能突变，在转子导条上会产生瞬时感应电流，以抵消合成气隙磁场的变化。转子感应电流产生的磁势相对于定子绕组以转速(1－s)w0旋转(s是转差率，w0为同步转速)，此时定子绕组中感应电动势E1的频率突变为(1－s)w0。断电后由于转速不断下降，导致E1的幅值和频率都不断减小。这个E1为感应电机的定子断电残余电压，简称断电残压［3］。

正常电机断电后，转子电流在定子绕组中产生的磁势主要为正弦波，谐波分量相对于基波来说很小，可以忽略。

当转子发生断条故障后，转子上的磁势波形发生畸变，使定子绕组上的感应电压发生变化，产生相应的谐波分量。在定子断电残压中，含有的谐波次数n为［1］

由于制造工艺的缺陷，即使正常的电机，在断电残压中也存在一定的上述谐波分量，只是这些分量相对较小。另一方面断电残压是一个时变信号，其频率和幅值都随时间不断衰减。因此对定子断电残压的谐波分量进行分析相当困难。

2 小波包熵理论

2.1 信息熵

信息熵是信源平均不确定性大小的度量，与

式中:M——信源状态总数;

ai——x可能取值［4］。

2.2 小波包理论

小波包变换是一种基于“频带”的时频分析方法，在高频范围内时间分辨率高，在低频范围内频率分辨率高，它通过多层次划分频带能够进一步分解细分高频部分，根据待分析信号的特点，自适应地选择合适的频段，与信号频谱相匹配，使频谱窗口进一步分割变细，以提高信号的分辨率，适合于故障电机的非平稳信号分析。

设正交小波基的滤波器系数分别为hn和gn，并将尺度函数φ(t)改记为w0(t)，小波函数ψ(t)改记为w1(t)，则关于φ(t)和ψ(t)的方程变为［5］信源可能出现的状态数目及各个状态出现的概率有关，熵越大说明系统越混乱，携带的信息越复杂，熵越小说明系统越有序，其携带的信息量越简单。

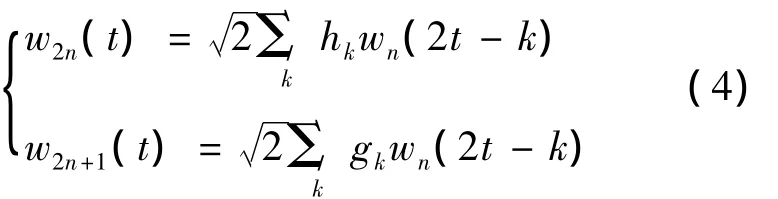
Shannon信息熵理论指出对于一个不确定的系统，若用一个取有限值的随机变量X表示其状态特征，取值ai的概率为P(x=ai)，则熵H定义为

由式(4)定义的函数集合wn(t{ })n∈Z称为由w0(t)=φ所确定的小波包。与小波分解相比，小波包变换增加了一个频率参数n。它用w2n和w2n+1将Wj空间分为相对低频和相对高频的两个子频带。通常对信号f作i次分解，一共可以分解得到的N=2i个子频带。当i=3时，小波包分解可以得到8个子频带，如图1所示。

2.3 小波包熵理论

结合小波包和信息熵给出小波包熵理论，对信号进行j层小波包分解可得到节点系数Sj，k，其中k=0，1，2……2j－1。设小波包系数的采样点数为N，由此得出第i个子频带小波包节点系数对应的能量Ej，k(i):

将各层子频带的节点系数能量作归一化处理得

图1 小波包树

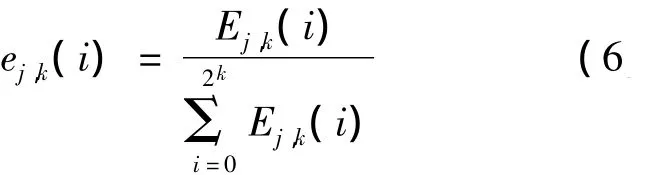
可以看出ej，k(i)是第i个子频带包含的信息能量在j层小波包上总能量中的概率，根据Shannon信息熵的基本理论，定义信号小波包分解的第j层k节点Sj，k的小波包熵Hj，k为［6］

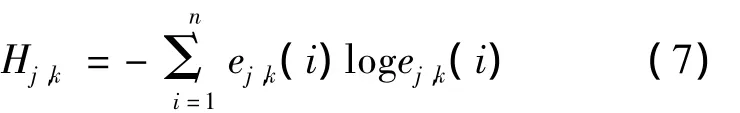
小波包分析反映了信号在时频域中能量分布情况，不同信号在时频分析上的差异表现为不同子块时频区间的能量分布差异，小波包熵理论是基于小波包分析方法建立起类似的信息熵理论，能够发现信息中微小的异常变化，实现低信噪比条件下提取弱信号和消除噪声，对时频域上的能量分布特性进行定量描述［4］。

发生转子断条故障后，断电残压信号中会出现相应的故障特征频率，故障特征频率的存在使信号不同频段的能量发生变化。应用小波包熵理论分析故障电机断电残压信号，可以清楚地反映出故障特征频率在信号不同频段中的分布情况，通过与正常电机断电残压信号作对比，判断故障是否发生。

3 仿真验证

感应电机断电后电压的幅值和频率是不断下降的，负载越大，断电残压的幅值和频率下降的速度越快，这样会影响信号的采样时间，给故障诊断带来困难。本文设电机失电前的状态为空载。

设信号采样频率为1 000 Hz，感应电机电源频率为50 Hz，由于断电残压信号随着时间不断衰减，为提高数据采样精度，采样时间应尽可能提前［3］，本文设为 0 ～0.2 s。图 2 为两种不同状态电机断电后的电压波形。

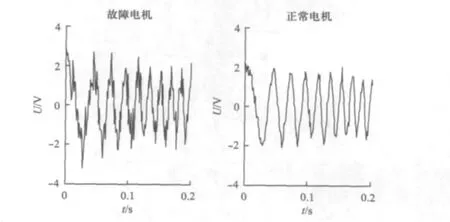
图2 断电残压波形

从图2可看出，发生转子断条故障后，由于相应谐波分量的存在，导致断电残压波形发生畸变。分别对转子断条故障电机和正常电机的断电残压进行频谱分析，得到的频谱如图3所示。

图3 断电残压频增

从图3可看出，发生转子断条故障后感应电机断电残压的频谱中除了基频分量外，5倍频分量和7倍频分量分别比正常电机断电残压频谱中的幅值大45%和90%。验证了转子断条故障特征频率在断电残压信号中的存在。

应用db1小波对感应电机断电残压信号进行3 层小波包变换，可以得到(3，0)，(3，1)…(3，7)共8个子频带，采样频率1 000 Hz，则得到的频带频率范围为(0 ～62.5 Hz)，(62.5 ～125 Hz)，(125 ～187.5 Hz)…，转子断条故障特征频率在(3，1)和(3，3)频段内。仿真结果如图4所示。

图4 小波包分解

通过图4中小波包分解后得到的3层和2层的低频系数及高频系数，可以看出:发生转子断条故障的感应电机中子频带系数均比正常电机的幅值要大，也就是说故障特征频率的存在使得子频带的能量发生了变化。应用Shannon小波熵理论得到故障电机和正常电机子频带的熵值，如表1所示。

表1 小波包Shannon熵值

从表1中可看出发生转子断条故障后电机断电残压小波包熵值中(3，1)段比正常电机熵值大，变化率为61%。这是由于故障特征频率在这个子频段中使得相应的子频带能量发生变化，信号中含有的信息量多，熵值增大，这就为感应电机转子断条故障诊断提供了新的理论依据。

4 结语

利用断电残压进行转子断条故障诊断，能够有效避免外界因素干扰;小波包分解是基于时频分析的有效工具，有效克服了非平稳信号高频段分辨率低的缺陷，小波包和Shannon熵理论相结合，得到的感应电机断电残压信号子频带的小波包熵值简单明了，熵值的变化率可作为故障诊断的依据。这为转子断条故障诊断提供了新的思路和方法。

［1］马宏忠.电机状态监测与故障诊断［M］.北京:机械工业出版社，2008.

［2］牛发亮.感应电机转子断条故障诊断方法研究［D］.杭州:浙江大学，2006.

［3］王轩.基于失电残压小波分析定子绕组故障诊断［J］.微特电机，2011(1):32-34.

［4］胡鹏.基于小波包熵的船舶轴频电场信号消噪研究［J］.应用基础与工程科学学报，2011，19(4):672-677.

［5］杨新华.基于小波分析的电机故障诊断研究［J］.电气自动化，2009，31(3):67-68.

［6］张亚楠.基于小波包Shannon熵SVM和遗传算法的电机机械故障诊断［J］.电力自动化设备，2010，30(1):87-91.