电网电压不对称跌落下双馈风力发电机机侧变频器控制策略的研究

邬冬临， 佘 岳， 徐凤星， 刘志星， 蒋耀生

(南车株洲电力机车研究所有限公司，湖南株洲 412001)

0 引言

由于变速恒频双馈感应风力发电机(Doubly Fed Induction Generator，DFIG)的优越性，使其在风力发电中得到广泛应用。但是，风能资源分布的特殊性使得风场接点处电网相对较薄弱，会在风力发电机连接点处出现电网电压不平衡现象。电网电压的不平衡会影响电机的运行状态，对整机产生不良影响，减少整机使用寿命，如不采取相应的控制措施将会影响电网的稳定性。因此，在电网电压不对称跌落下如何控制DFIG的运行，已成为国内外风电技术以及各整机制造商研究的重点［1-4］。目前，关于这方面的研究策略主要是通过电机的转子电流或转子电压，从双馈电机本身的控制实现双馈电机的抗电网电压不平衡运行特性。本文在传统的定子磁链定向矢量的基础上通过加入电流谐振调节器来控制转子电流。仿真结果和试验波形能够证明，本文所提出的电流谐振控制策略，在电网电压不对称跌落时能够很好地控制转子电流，提高DFIG发电机组运行的可靠性。

1 双馈风力发电机系统数学模型

变速恒频DFIG风力发电系统原理框图如图1所示。从图1可看出，DFIG发电机组主要由风力机、齿轮箱、控制电路、变频器和变压器等组成。

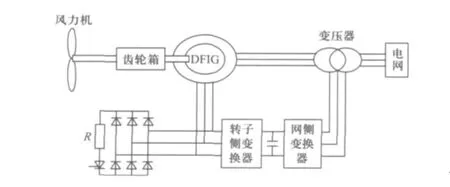
图1 变速恒频DFIG风力发电系统示意图

按电动机惯例，同步旋转坐标系下DFIG的电压方程为

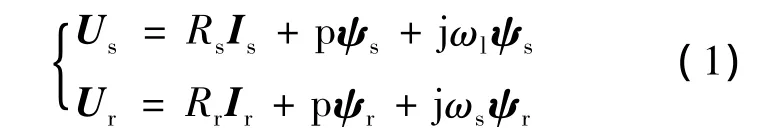
式中:Us、Ur——定、转子电压矢量;

Is、Ir——定、转子电流矢量;

ψs、ψr——定、转子磁链矢量;

Rs、Rr——定、转子电阻;

Ls，Lr——定、转子绕组全自感，Ls=Lsσ+Lm，Lr=Lrσ+Lm;

Lsσ、Lrσ、Lm——定子漏感、转子漏感和定、转子间的互感;

ωl——同步电角速度;

ωs——滑差角速度，ωs=ωl－ωr;

ωr——转子旋转电角速度。

其磁链方程为

2 比例-谐振控制器的提出

2.1 电网电压不平衡下双馈发电机的数学模型

当电网电压发生不平衡故障时，DFIG发出的功率不能及时送出，在定子侧将会产生很大的故障电流。由于定子和转子之间存在的强耦合关系，故障电流被传递到转子侧，在电网电压发生不平衡时会导致运行滑差增大，电磁转矩变小，使馈入转子的功率增加，致使转子侧的电流和电压增加，大电流又会导致电抗减少、电机铁心饱和，实际上转子电流还会加大。在电网电压不对称跌落时，转子电流除了含有基波成分外，还包含谐波频率为二倍频的谐波成分。在电网电压不平衡条件下，两相静止αβ坐标系中矢量形式的DFIG定、转子电压和磁链方程分别为

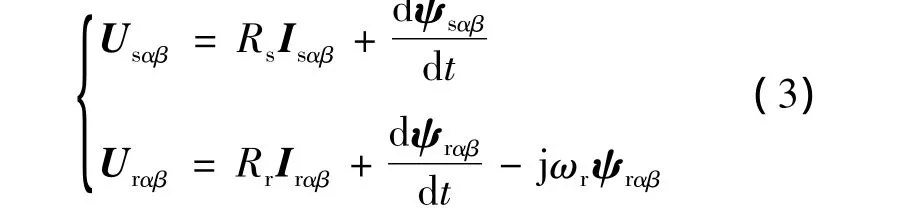
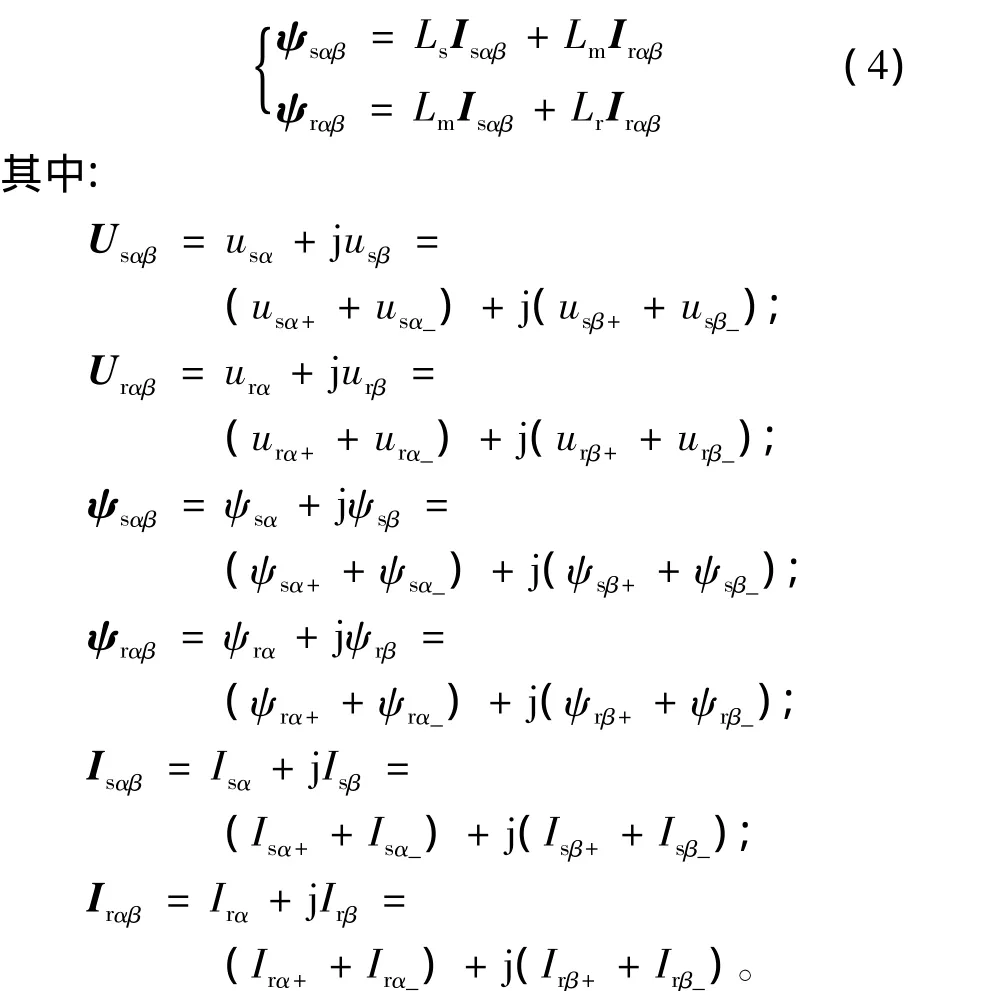
在上式中以各自正、负序分量分别表达的静止αβ坐标系中定、转子电压、电流和磁链方程:

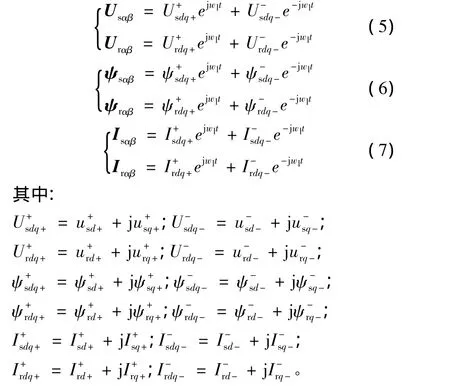
将式(5)～式(7)代入式(3)和式(4)，并经过整理，可得正、反转同步速度旋转dq+、dq－坐标系中分别由各自正、负序分量表示的DFIG电压、磁链方程。

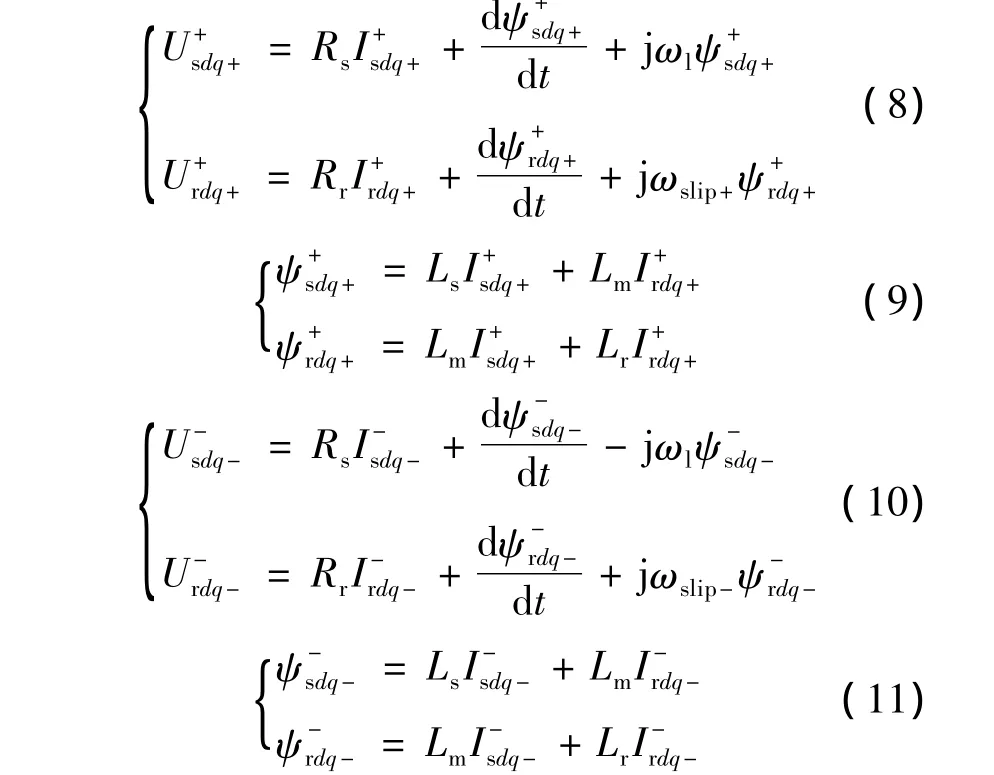
式中:ωslip+——正转滑差角频率，ωslip+=ωl－ωr;

ωslip－——反转滑差角频率，ωslip－=－ωl－ωr。

式(9)和式(11)表明，电网电压不平衡时可以有转子电流的正、负序分量作为可控变量，即:、，通过对转子电流运行能力控制策略，可以降低不平衡电网电压时，负序电压对DFIG系统的不利影响，提高不对称电网电压故障下DFIG风电机组的不间断运行能力。

2.2 PR控制器的定义

由于在电网电压产生不平衡故障时，转子侧将会产生较大的冲击电流，如何控制在电网电压不平衡时的转子侧电流是目前风电技术研究的重点之一。本文将研究不平衡电网电压条件下，DFIG转子侧变换器的设计和性能评估，并给出仿真结果和验证试验波形。逆变器输出波形的质量及动静态性能是衡量逆变器性能优劣的重要依据。由于负载的多变性，简单的开环控制不能满足对动态响应的要求，为了能够实时调控逆变器的输出波形，提高逆变器性能，引入各种实时反馈控制方法对逆变器输出的波形进行控制。因此模糊控制、重复控制、谐波反馈控制及滑模变结构控制等各种高性能的波形控制技术迅速发展起来。虽然PI控制器具有较快的动态响应特性和鲁棒性等优点，但是在交流系统的反馈控制时，PI控制并不能实现无静差控制。由于比例谐振控制器能够直接控制交流量，并且具有非常好的稳态和瞬时性能［5-7］，为了能够提高对转子侧电流波形的控制，本文采用了比例-谐振控制器。比例-谐振控制器直接通过控制交流量来消除稳态误差的目的，其数学传递函数为

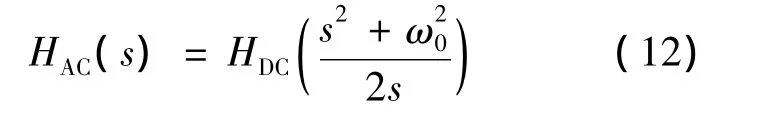
式中:ω0——谐振角频率，在此为 100 π(工频为50 Hz)。

式(12)的转换原理是把一个期望的直流补偿器转换成一个等价的交流补偿器，并且使它们在带宽范围内具有相同的频率响应。由于模拟系统中的部件误差以及数字系统中有限的精确度，直流补偿器通常用一个低通传递函数来表示

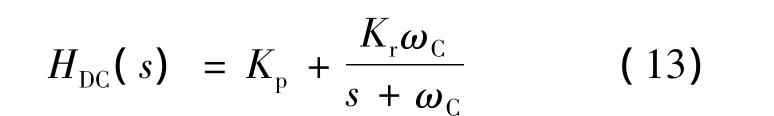
式中:ωC——直流补偿器的截止频率。

将式(13)代入式(12)得到比例-谐振(PR)控制器为

当电网电压发生不平衡时，双馈发电机(DFIG)数学模型中存在交流分量，在正序dq坐标系下为2倍频交流量。根据比例-谐振控制器对交流量的直接控制特点，将其引入常规的双馈风力发电机的控制中。

3 加入谐振控制器的DFIG机侧控制策略

DFIG在dq坐标系下电压方程为

根据电机磁通定义:

根据转子侧励磁控制策略［8］，可以大大提高风电机组在电网发生跌落情况下的不间断运行能力。采用定子磁链定向，定义定子磁链为旋转坐标系的d轴，即ψsq=0，将式(16)代入式(15)，得到正序坐标系下包含正负序的转子电压方程:

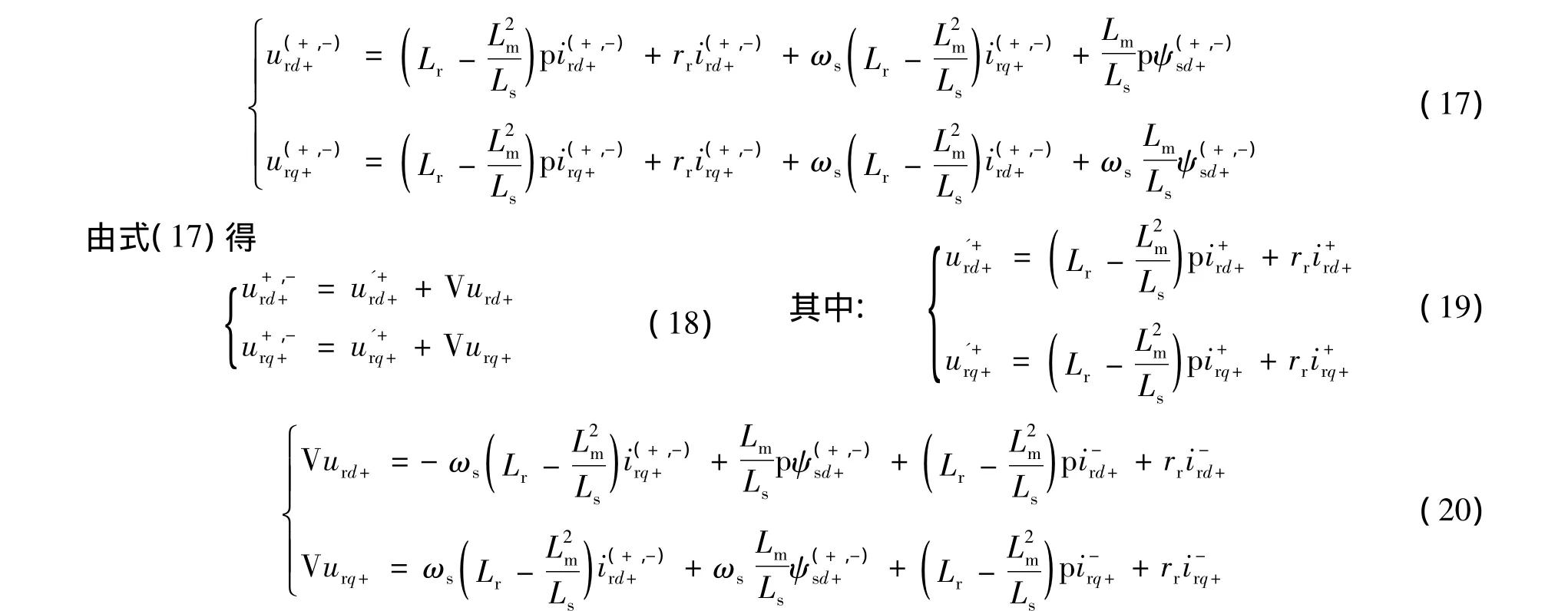
Vurd+、Vurq+——两倍频电网电压的补偿项。

将式(18)作为电网电压不对称跌落时，双馈风力发电机控制策略的实现依据与传统的矢量控制策略相比较，改进后的控制策略是在原来的基础上增加转子电压两倍频补偿项Vurd+、Vurq+，可以通过比例-谐振控制器无差跟踪实现。由以上DFIG的数学模型可推导出电网电压不平衡跌落时的控制框图如图2所示。

图2 电网电压不平衡跌落时的控制系统框图

4 仿真分析及试验结果

为了验证本文提出的对转子侧变流器转子电流加入的谐振控制，能够在电网电压不平衡时对转子电流进行有效控制。本文采用PSIM仿真软件进行仿真验证，并在1.65 MW风机功率试验台上进行试验。在PSIM仿真软件中搭建的1.65 MW双馈风力发电机模型，系统仿真参数如下:额定电压UN=690V，额定功率PN=1.65 MW，额定频率f=50 Hz，定子绕组电阻Rs=0.007 84 Ω，转子绕组电阻Rr=0.005 9 Ω，定子绕组漏感Lsσ=0.053 Ω，转子绕组漏感Lrσ=0.062 Ω，互感Lm=3.71 Ω，极对数p=2，直流母线电压Udc=1 150 V，选取 RCrowbar=0.2 Ω。在仿真试验中分别在电网电压单相跌落33%时，对转子电流进行不加入谐振控制和加入谐振控制进行仿真，仿真波形如图3、图4所示。

图3 在单相电压跌落33%时对转子电流不加入谐振控制的电网电压波形图和转子电流波形图

在1.65 MW风机功率试验台上，当电网单相电压跌落33%时，分别对转子电流不加入谐振控制和加入谐振控制得到的转子电流试验波形，如图5、图6所示。

图4 在单相电压跌落33%时对转子电流加入谐振控制的电网电压波形图和转子电流波形图

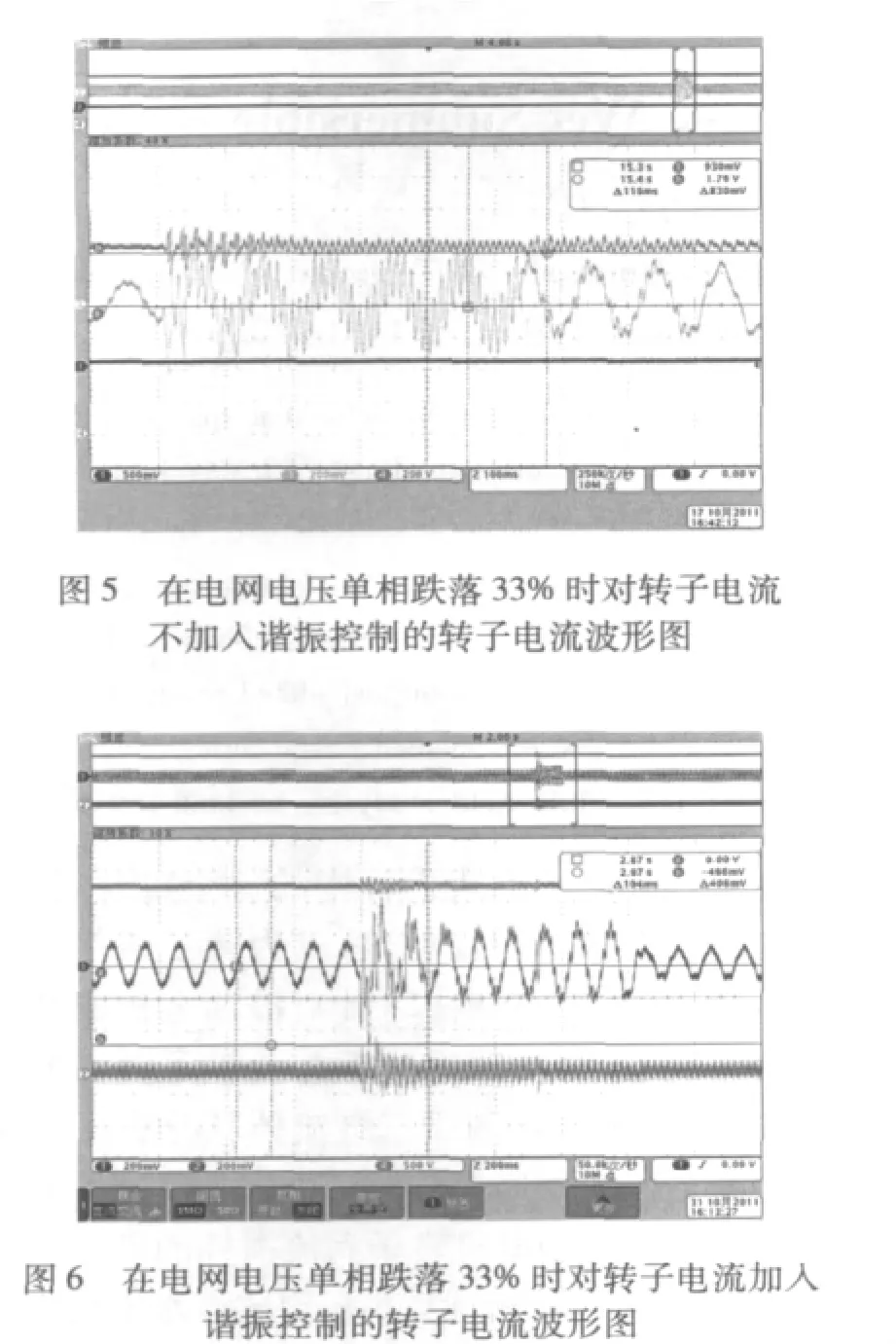
从仿真图3和试验波形图5可看出，在电网电压单相跌落33%时，对转子电流不加入比例-谐振控制，转子电流将会产生较大的谐波，并且容易产生转子侧过流故障，影响风机在电网电压不平衡时的不间断运行能力。从仿真图4和试验波形图6中可看出，在电网电压单相跌落33%时，加入对转子电流的谐振控制后，能够对转子电流的谐波进行较好的控制，以实现波形控制，实时地调控输出的电流波形，提高逆变器的质量，快速减少电流的振荡，具有快速限流的保护能力，使整机系统的可靠性得到提高。

5 结语

针对PI控制器在瞬时值反馈控制中不能完全消除交流系统稳态误差的问题，本文提出了在不平衡电网电压条件下DFIG风电机组用比例-谐振(PR)控制器方案。在电网电压不对称跌落时，该谐振控制器能够对转子侧变换器交流实现有效、快速调节控制，并且能够对降低转子电流的过流产生较好控制。仿真结果和试验结果有力表明比例-谐振电流控制方案能够在电网电压不平衡时实现既定的控制目标。在电网电压不平衡故障时具备良好的调节性能，有效保障和增强了在不平衡电网电压故障下DFIG风电机组的故障穿越(不间断)运行能力。因此，在实际的DFIG风电机组运行中具有相当实用的工程应用价值。由于变流器容量和器件耐压等级等因素的限制，在电网电压严重不平衡情况下的谐振控制，以及怎样通过谐振控制减少电网电压不平衡下电机转矩脉动是下一步工作研究的重点。

［1］MORREN J，SJOERD W H.Ridethrough of wind turbines with doubly-fed induction generator during a voltage dip［J］.IEEE Trans Energy Convers，2005，20(2):435-441.

［2］胡家兵，孙丹，贺益康，等.电网电压骤降故障下双馈风力发电机建模与控制［J］.电力系统自动化，2006，30(8):21-26.

［3］SUN T，CHEN Z，BLAABERG F.Voltage recovery of grid-connected wind turbines and DEIG after a short-circuit fault［C］∥ Institute of Electrical and Electronics Engineers Inc， Piscataway， United States，2004:1991-1997.

［4］LOPEZ J， SANCHISP， ROBOAM X， etal.Dynamicbehaviorofthe doubly fed induction generator during three-phase voltage dips［J］.IEEE Trans Energy Convers，2007，22(3):709-717.

［5］ZMOOD D N，HOLMES D G，BODE G.Frequency domain analysis ofthree phase linear current regulators［J］.IEEE Trans Ind Applicat，2001，37(2):601-610.

［6］LOH P C，NEWMAN M J，ZMOOD D N，et al.Improved transient and steady state voltage regulation for single and three phase uninterruptible power supplies［C］∥PESC-IEEE Annual Power Electronics Specialists Conference，2001(2):498-503.

［7］LOH P C，NEWMAN M J，ZMOOD D N，et al.A comparative analysis of multilooop voltage regulation strategies for single and three-phase UPS systems［J］.IEEE Trans PowerElectron，2003，18(5):1176-1769.

［8］ZMOOD D N，HOLMES D G.Stationary frame current regulation of PWM inverters with zero steady state error［J］.IEEE Trans Power Electron，2003，18(3):816-817.