《几何画板》的应用价值之我见
2012-08-28河南省固始县慈济高中
☉河南省固始县慈济高中 吴 强
当前,践行“科学发展观”已成时代主题.在这个信息技术日新月异的时代,教师应时刻思考用先进技术手段改进教学方法,并发展、升华教育思想,实现教育教学的科学发展.《几何画板》作为一款优秀的教学软件,虽然早已面世,但很多教师出于认识或条件所限,并未将其真正应用于教学.本文着重介绍笔者在教学中应用该软件的心得和收获,以期引起思索和共鸣,并让更多同仁投身于教改和信息技术应用中来.
形象思维在学习和研究中都起着重要作用,一个学生如果不具备良好的数学形象思维能力,不可能学好数学.数学家柯尔莫哥洛夫曾说:“只要有可能,数学家总是尽力把他们正在研究的问题从几何上视觉化.”因此,随着信息技术的发展并广泛应用于各个领域,也给课堂教学带来了深刻变革——用计算机辅助教学,改善学生的认知环境已成为必然趋势.《几何画板》以其门槛不高和操作方便的优点,及强大的图形处理能力、易用的动画功能被国内外专家、教师推崇,并成为制作数学课件的主流软件之一.其应用价值主要体现在以下方面.
一、《几何画板》让代数教学图形化、直观化
“数形结合”一直是高中数学中的一个重要思维方法,而对其运用最广泛的莫过于函数部分.“函数”的思维和分析方法渗透在高中数学的各个章节;同时,函数是以运动、变化的观点对现实世界数量关系作出刻画,这又决定了它是对学生进行素质教育的重要载体.函数的两种表达方式——解析式和图像之间常常需要比照、融合(如研究函数的单调性、讨论方程或不等式的解的情况等).在函数的传统教学中,教师多用手工绘图,但手工绘图有不精确、效率低的弊端.而应用《几何画板》精准直观的展示及变化功能则可以克服上述弊端,大大提高教学效果和课堂效率,起到事半功倍的效果.
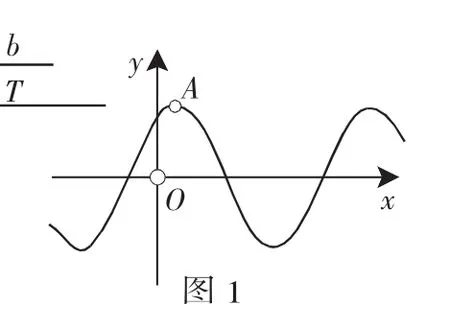
例如,利用《几何画板》作图功能,在同一个直角坐标系中作出函数y的图像,通过各自图像特点,比较其位置和变化规律,归纳幂函数的性质.同时《几何画板》还可以作出含有若干参数的函数图像,当参数变化时函数图像也相应地变化,如在讲函数y=Asin(ωx+φ)的图像时,传统教学只能将A、ω、φ代入有限个值,观察各种情况的函数图像之间的关系;而利用《几何画板》则可以以线段b、T的长度和A点到x轴的距离为参数作图(如图1),当拖动两条线段的某一端点(即改变两条线段的长度)时分别改变三角函数的初相和周期,拖动点A则改变其振幅,达到动态演示.这样在教学时既快速灵活、形象直观,又不失一般性.
二、《几何画板》让立体几何教学更加高效、精准
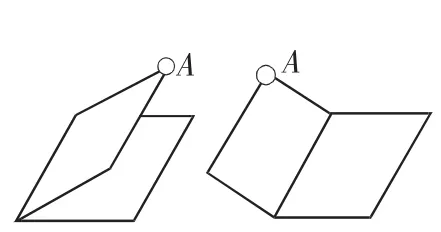
图2
立体几何是在平面图形分析的基础上讨论空间图形的性质.从平面观念过渡到立体观念,无疑是认识上的一次飞跃.初学立体几何时,大多数学生不具备丰富的空间想象力及较强的平面到空间的图形转化能力,这给学生学习立体几何增加了困难.而应用《几何画板》将图形动起来,就可以使图形中各元素之间的位置比照和度量关系惟妙惟肖,能让学生从多个不同的角度去观察图形.这样,不仅可以帮助学生理解和接受立体几何知识,还可以让学生的想象力和创造力得到充分的发挥.
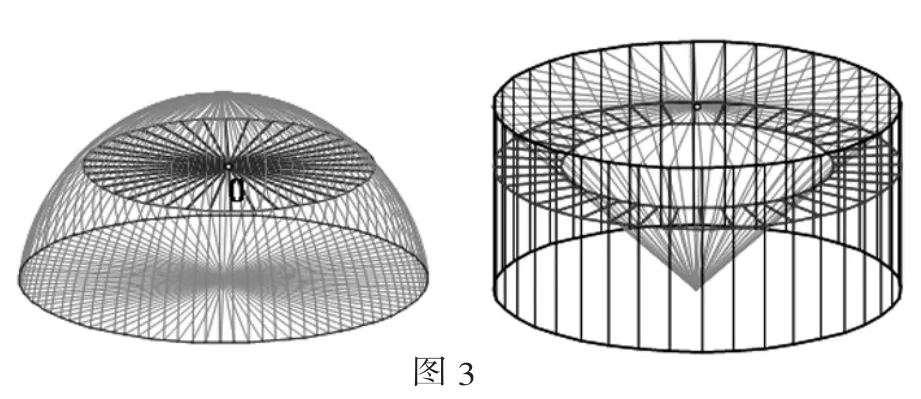
像在讲二面角的定义时(如图2),当拖动点A时,点A所在的半平面也随之转动,改变了二面角的大小.生动直观的图形变动有利于帮助学生建立空间思想和培养空间想象力;在演示用祖暅原理推导球体积公式时,运用动画和
轨迹功能作图3,过O作球和柱、锥的水平截面,当上下拖动点O时,让学生观察此过程中两个几何体相应截面的变化规律和内在联系,并在预习教材的基础上论证所截得的两截面面积之和为定值,进而自主应用祖暅原理推导出球体积公式.这样的教学设计能让学生产生浓厚兴趣和强烈求知欲,同时美丽生动的画面在学生学得知识的同时,给人以美的感受,创建一个轻松、乐学的氛围.
三、《几何画板》让平面解析几何更加生动形象
平面解析几何是用代数方法来研究几何问题的一门数学学科,展示几何图形变化与运动的动态过程在解析几何教学中是非常重要的.《几何画板》又以其极强的运算功能和图形分析处理功能在解析几何中大显身手.比如它能作出各种形式的方程(普通方程、参数方程、极坐标方程)的曲线;能对动态的对象进行“追踪”,并显示该对象的“轨迹”;能通过拖动某一对象(如点、线)观察整个图形的变化来研究两个或两个以上曲线的位置关系.
例如在讲椭圆的定义时,可以由“到两定点F1、F2的距离之和为定值的点的轨迹”入手——如图4,在几何画板上令线段AB的长为“定值”,在线段AB上取一点E,再分别以F1为圆心、AE的长为半径和以F2为圆心、BE的长为半径作圆.然后拖动点E,使得两圆半径随之变化但半径和为定值,大家可以自主发现两圆的交点轨迹即符合要求的研究对象.
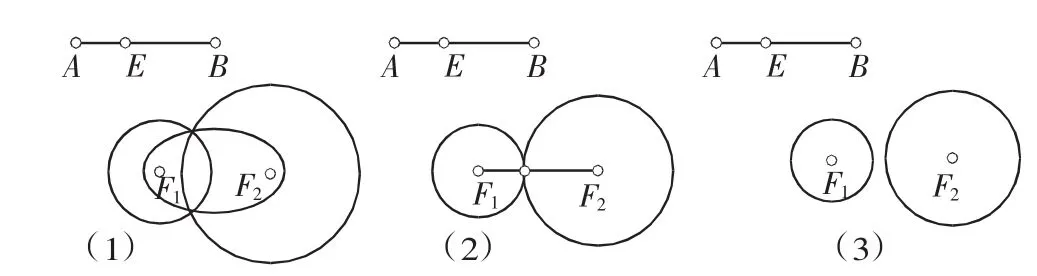
图4
先让学生猜测这样的点的轨迹是什么图形,学生各抒己见之后,老师动态演示图4(1),学生豁然开朗:“原来是椭圆!”.这时老师用鼠标拖动点B(即改变线段AB的长),使得|AB|=|F1F2|,如图4(2),满足条件的点的轨迹变成了一条线段F1F2,学生开始谨慎起来并主动思索,接下来不难得出图4(3)(|AB|<|F1F2|时)的情形,随后请大家自主归纳这三类情况之间的区别与联系.经过上述过程,学生不仅深刻地掌握了椭圆的概念,也锻炼了其思维的缜密性,强化了分类思想.
综上所述,使用《几何画板》进行数学教学,通过形象的感性信息呈现,给学生留下更为深刻的印象,使学生不再是把数学作为单纯的知识去理解记忆,而是能够更有实感地去体会、把握.这样,既能激发学生的情感、培养学生的兴趣,又能大大提高课堂效率,取得良好教学效果.
1.姚淑华,李孝诚.《几何画板在中学数学教学中应用模式的探讨》.《电脑知识与技术》,2008年30期.
2.陶维林.《几何画板实用范例教程(第2版)》,清华大学出版社出版,2008-07-01.
