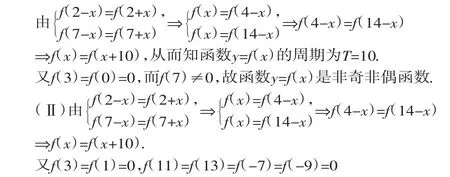方程搭台 函数“唱戏”
2012-08-28江苏省沭阳如东中学高安军
☉江苏省沭阳如东中学 高安军
函数和方程有着千丝万缕的联系,在近年的高考中,频频出现一些方程和函数结合起来的题目,在解答时,主要是利用函数的特性来解,下面举例说明.
A.4 B.5 C.7 D.8
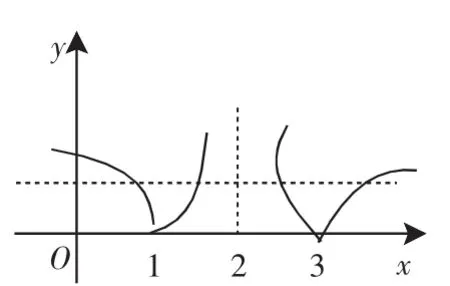
解析:方程f2(x)+bf(x)=0可化为f(x)=0或f(x)=-b.而y=f(x)的图像大致如图所示.
由图可知,直线y=0(即x轴)与y=f(x)的图像有3个交点,直线y=-b(b<0)与y=f(x)的图像有4个交点,即方程f(x)=0有3个实根,方程f(x)=-b有4个实根,从而原方程共有7个实根,故答案选C.
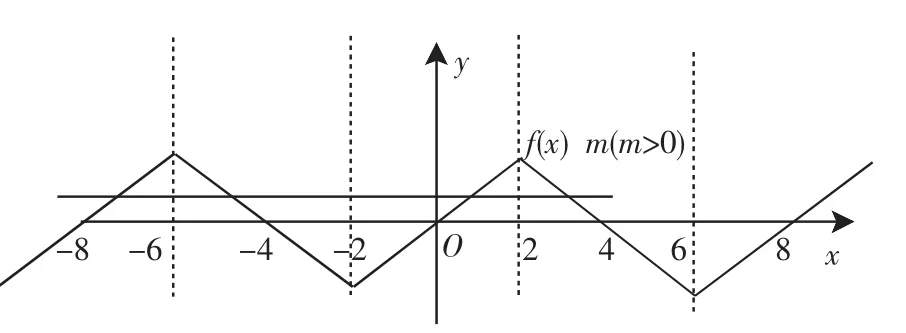
例2已知定义在R上的奇函数f(x),满足f(x-4)=-f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=__________.
解析:因为定义在R上的奇函数f(x),满足f(x-4)=-f(x),所以f(x-4)=f(-x).由f(x)为奇函数,所以函数图像关于直线x=2对称且f(0)=0,由f(x-4)=-f(x)知f(x-8)=f(x),所以函数是以8为周期的周期函数.又因为f(x)在区间[0,2]上是增函数,所以f(x)在区间[-2,0]上也是增函数.如图所示,那么方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,不妨设x1 图1 图2 评注:本题综合考查了函数的奇偶性,单调性,对称性,周期性,以及由函数图像解答方程问题,运用数形结合的思想和函数与方程的思想解答问题. 图3 例4 设a>1,若仅有一个常数c使得对于任意的x∈[a,2a],都有y∈[a,a2]满足方程logax+logay=c,这时a的取值的集合为__________. 分析:题目给出的方程中含有x,y,a,c等多个字母,而条件中是对任意的x∈[a,2a]都有y∈[a,a2],这使我们联想到函数的定义域、值域,所以必须把方程改写为关于y的函数,再进一步研究函数的性质. 例5设函数f(x)在(-∞,+∞)上满足f(2-x)=f(2+x),f(7-x)=f(7+x),且在闭区间[0,7]上,只有f(1)=f(3)=0. (Ⅰ)试判断函数y=f(x)的奇偶性. (Ⅱ)试求方程f(x)=0在闭区间[-2005,2005]上的根的个数,并证明你的结论. 解:(Ⅰ)由f(2-x)=f(2+x),f(7-x)=f(7+x)得函数y=f(x)的对称轴为x=2和x=7, 从而知函数y=f(x)不是奇函数. 故f(x)在[0,10]和[-10,0]上均有两个解,从而可知函数y=f(x)在[0,2005]上有402个解,在[-2005,0]上有400个解,所以函数y=f(x)在[-2005,2005]上有802个解.