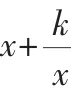对2012年高考湖北卷(理科)压轴题的思考
2012-08-28江苏省灌云县杨集中学
中学数学杂志 2012年23期
☉江苏省灌云县杨集中学 苏 勇
对2012年高考湖北卷(理科)压轴题的思考
☉江苏省灌云县杨集中学 苏 勇
题目:(2012年高考湖北卷(理科)压轴题)(Ⅰ)已知函数f(x)=rx-xr+(1-r)(x>0),其中r为有理数,且0<r<1.求f(x)的最小值.
(Ⅱ)试用(Ⅰ)的结果证明如下命题:设a1≥0,a2≥0,b1,b2为正有理数,若b1+b2=1,则a1a2≤a1b1+a2b2.
(Ⅲ)请将(Ⅱ)中的命题推广到一般形式,并用数学归纳法证明你所推广的命题.
注:当α为正有理数时,有求导公式(xα)′=αxα-1.
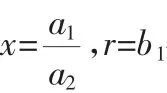
例1 (2012年高考湖南卷(理科)第22题)已知函数f(x)=eax-x,其中a≠0.
(1)若对一切x∈R,f(x)≥1恒成立,求a的取值范围.
(2)在函数f(x)的图像上取定两点A(x1,f(x1)),B(x2,f(x2))(x1<x2),记直线AB的斜率为k.问:是否存在x0∈(x1,x2),使f′(x0)>k成立?若存在,求x0的取值范围;若不存在,请说明理由.
下面给出(2)的解答: