探索性问题的几种类型与求解策略

☉广东省中山市东升中学 郭 华

探索性问题的几种类型与求解策略

☉广东省中山市东升中学 郭 华

探索性问题是指没有明确的结论，需要经过分析、推断、计算并加以证明的一种新题型.由于这类问题题型新颖，涉及面广，综合性强，难度大，不但能考查学生的基础知识，而且能从较高层次上考查学生的创造性思维能力和发现问题、提出问题、分析问题并解决问题的能力，一直受到高考命题者的青睐.探索性问题常以不同的形式出现在每年的高考数学压轴题当中，因而扮演着重要的角色，很多考生往往无从下笔.

从笔者多年的工作中所收集和整理的一些高考题来看，高考探索型问题主要有以下三种类型：（1）猜想归纳型，（2）存在型，（3）分类讨论型.下面通过举例谈谈这类问题的解题策略.

一、猜想归纳型

猜想归纳型探索问题的解题思路是：从最简单、最特殊的情况出发，推测出结论，再进行严格的证明.

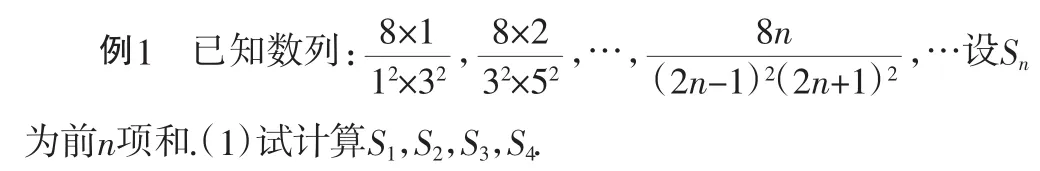
（2）根据所求结果，推测出Sn的计算公式，并用数学归纳法加以证明.

由此可知，当n=k+1时等式也成立.

根据①②可知，等式对任何n∈N都成立.

评析：本题考查观察、分析、归纳的能力和数学归纳法，是一道典型的猜想、归纳型探索性试题.

二、存在型

对于结论没有明确给出，常常以“是否存在”“是否有”的形式进行提问，暗示结论有待判断，这类问题我们称之为存在性问题.

存在型问题的解题思路是：先假设结论存在，若推证无矛盾，则结论成立；若推证出矛盾，则结论不存在.分析法和反证法在解题中起着关键作用.

例2 设{an}是由正数组成的等比数列，Sn为前n项和.

由此可知，不满足条件①，即不存在常数c＞0使结论成立.

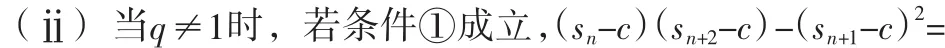
三、分类讨论型

当问题的对象不能进行统一研究时，就需要对研究的对象进行分类，然后对每一类分别研究，给出每一类的结果，最后综合各类结果得到整个问题的解答.因此需搞清楚引起分类讨论的原因是什么，在分类探索的过程中应注意分类原则：（1）对所讨论的全域分类要“既不重复，也不遗漏”.（2）在同一次讨论中只能按所确定的一个标准进行.（3）对多级讨论，应逐级进行，不能越级，层次分明是分类讨论的基本要求.

例3 已知数列{an}和{bn}满足：a1=b1=1+lga，a2=b2=（1+lga）lga.当n≥2时，a2，a3，...，an，...是以（1+lga）为公比的等比数列，b2，b3，…，bn，…是以lg2a为公差的等差数列，{an}和{bn}的前n项和分别为sn和Tn.当a＞且a≠1时，试比较s和T的大小关系并证明你的结论.nn

猜想当n≥3时，sn＜Tn，下面用数学归纳法加以证明.

①n=3时，已证S3＜T3正确.

评析：这是一道典型的分类讨论探索性问题，结论不确定，需分n=1，n=2；n≥3.这两大类进行讨论.而当n≥3时又要分a＞1和＜a＜1两种情形讨论.从而问题得以完美解答.正是这类问题包含的数学思想丰富，技巧性强，书写解答的量大，考生如果没有解题信心是很难出色完成任务.

从以上举例可以发现，凡是解答探索性问题都遵循从一般到特殊、到猜想证明、再到分类讨论、最后到归纳总结这一认识事物的基本规律，这其中数学归纳法扮演着重要的角色.事实证明，学好数学归纳法和善于分类讨论以及养成良好的总结习惯是解决这 类较高思维层次试题的根本前提.