一道课本习题的 一题多变
2012-08-28江苏省泰州中学郑丽年
☉江苏省泰州中学 郑丽年
一道课本习题的 一题多变
☉江苏省泰州中学 郑丽年
数学,作为一种科学和艺术,从本质上反映了自然界的五彩缤纷、绚丽多彩;但是作为一门学科,它的大部分内容却显得抽象和乏味.
高中数学内容多,容量大,老师在上课的时候,生怕学生见的题型少,拼命在课堂上给学生灌很多的题目,让学生在题海中奔波,没有了自己的见解,导致一部分学生在考试时出现了“不怕难,就怕新”的怪现象.
笔者认为能否运用所学知识解决问题关键还在于有没有真正地理解这个知识点,道家有句话叫做道生一,一生二,二生三,三生无穷,也就是平时说的“悟”,这样的要求对很多学生都比较高,这就需要老师在平时教学过程中有意识的加强这方面的训练.
例如课本上有这么一道题:
例题 求曲线y=x3+3x在点P(-2,-14)处的切线方程.
解:令f(x)=x3+3x.因f′(x)=3x2+3,则f′(-2)=15,故所求切线方程为y=15x+16.
这道题目本身比较平淡,如果我们上课时也仅仅是点到为止,那么学生根本就不感兴趣,也失去了这道题目的潜在的解题功能,现在我们做一些小小的变化.
变题1:已知曲线C:f(x)=x3-x+2,求经过点P(1,2)的曲线C的切线方程.

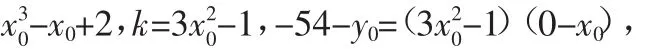

变题4:斜率为3的直线与曲线C:y=x3相切于P点,并与曲线有另一个交点Q,求两点P、Q的坐标.
解:因y′=3x2,k=3,故xP=±1,切点坐标为(1,1)或(-1,-1).
当切点为P(1,1)时,切线方程为y=3x-2,得另一点Q的坐标为(-2,-8);当切点坐标为P(-1,-1)时,同理可得Q(2,8).
变题5:P为曲线C:y=x3上一动点,若曲线在点P处的切线与曲线有另一交点Q,求PQ的中点的轨迹方程.
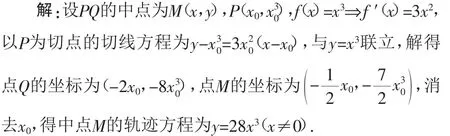
挖掘教材习题的潜在功能,有利于活跃学生的思维,拓广思路,长期坚持下去,有利于学生智力的发展,解题能力的提高,也有利于避免题海战术,减轻学生的负担.
