挖掘赵爽弦图的导入功能:信息技术使数学史熠熠生辉的一则案例
2012-08-28华中师范大学数学与统计学院徐章韬
☉华中师范大学数学与统计学院 徐章韬
挖掘赵爽弦图的导入功能:信息技术使数学史熠熠生辉的一则案例
☉华中师范大学数学与统计学院 徐章韬
*本文系中国博士后科学基金第五批特别资助 “信息技术推动数学历史文化走进数学课堂之研究”(编号:2012T50656)的部分成果.
一、引言
最近,张奠宙先生指出:导入和创设情境是有区别的,不可能在每堂课都创设情境,创设情境不能天天搞.而导入则是每堂课都能进行的.导入的价值和实行的办法是要思考的问题.导入强于创设情境,导入作为艺术在中国已经成形了,导入的价值和施行方法应该立起来.每节课都要引入[1].张先生的话从大处着眼,高屋建瓴.要把张先生的思想落到实处,就要从小处着手,从近处着手.用数学史作课堂教学的引子是个不错的主张.但数学史的运用绝不仅仅限于用有趣的历史故事吸引学生,而是要充分挖掘历史文化的底蕴.若能用信息技术使数学史的文化底蕴动态地、形象地揭示出来,将是一件“锦上添花”的事情:浓郁的历史文化氛围与现代文明跨时空地交织在一起,历史文化使思想更深邃,信息技术使思想更完美.本文在吃透赵爽弦图的基础上,深入挖掘赵爽弦图的导入功能,以期抛砖引玉,以期在信息技术的支持下,更多的历史文化能更好地融入到课堂教学之中.
二、吃透历史:以形证数、形数统一的赵爽弦图
三国时期的数学家赵爽是最早对勾股定理进行证明的人.赵爽创制了一幅“勾股圆方图”(如图1),用形数结合得到方法,并给出了勾股定理的详细证明.在“勾股圆方图”中,以弦为边长的正方形ABDE是由4个全等的直角三角形再加上中间的小正方形组成的.每个直角三角形的面积为ab;中间的小正方形边长为b-a,面积为(b-a)2.于是便可得如下的式子+(b-a)2=c2,化简即得,a2+b2=c2.
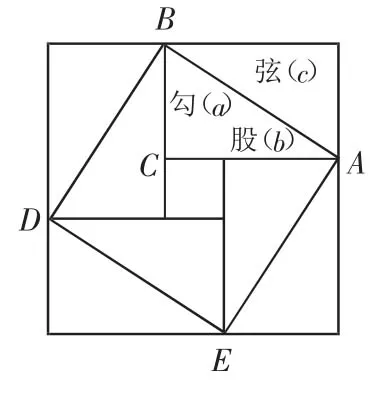
图1 勾股圆方图
赵爽的证明别具匠心,极富创新意识:用几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范.以后的数学家大多继承了这一风格并且屡有发展.例如,稍后一点的刘徽在证明勾股定理时用的也是以形证数的方法,只是具体图形的分、合、移、补略有不同而已.
中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位.尤其是其中体现出来的“形数统一”的思想方法,更具有科学创新的重大意义.事实上,“形数统一”的思想方法正是数学发展的一个极其重要的条件.正如吴文俊先生所说:“在中国的传统数学中,数量关系与空间形式往往是形影不离地并肩发展着的……十七世纪笛卡儿解析几何的发明,正是中国这种传统思想与方法在几百年停顿后的重现与继续.”
华罗庚先生指出:“数形本是相倚依,焉能分作两边飞;数缺形时少直观,形少数时难入微;数形结合百般好,隔裂分家万事休.”形数结合,让抽象的数栖居在形之上,用解析的数描述形的特征,坚持抽象性与直观性的统一其实是一条教学原则.
三、技术使历史熠熠生辉:赵爽弦图是很好的导入载体
1.完全平方和公式、完全平方差公式的导入
人教社的教材先举出计算几个整式的乘法的实例,然后归结出完全平方和、完全平方差公式.接着教材又给出图2说明完全平方和公式.

图2 人教社教材中的完全平方和(差)公式的说明图
这是从代数的角度来引入的,图形起辅助说明.其优点在于和前面的整式乘法的知识衔接紧密,不足之处是文化味儿少了一点儿,没有充分体现“以形证数,形数统一”的思想.
赵爽弦图是我国古代的优秀文化遗产,其中闪烁着智慧的光芒迄今仍不过时.我们设想,在介绍一个公式、定理之前,先要让学生直观感知,然后再让学生形式化地证明,可能更符合认知规律.基于上述认识,用超级画板制作了下面的动画(如图3).
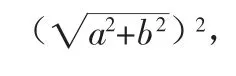

图3 赵爽弦图背景中的平方差公式和重要不等式

点击动画,还可以看到下面的情形(如图4).

图4 赵弦弦图背景中的平方和公式
这里,一幅图的两种状态分别表征了平方和公式与平方差公式,这表明这两个公式其实是一回事!这是从图形连续变化角度得出来的结论,从代数的角度看,更是如此!初学代数的同学不容易看到这一点,不能把-b看做b,不能理解代数的精髓,现代信息技术使我们慢慢地接受这种观点,信息技术能改变同学们对数学的看法.
因此,完全平方和、平方差公式的导入流程可以是:演示动画——计算面积关系——得到公式——验证公式.这样,学生经历感知——观察——说理——直观论证这样一个完整的学习路线.这种引入法完全符合新课程理念.整个过程如图5所示.

图5 引入过程和学生的学习过程
2.重要不等式的引入
人教社教材是由直接展开(a-b)2=a2+b2-2ab,再利用平方数的非负性得到重要不等式的.并由图6给出了重要不等式的图解.
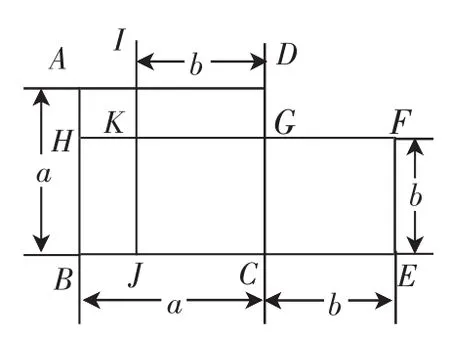
图6
而从赵爽导出重要不等式,既为重要不等式配置了图形背景,也为重要不等式注入了文化的气息,而且赵爽弦图美于图6.

图7 赵爽弦图背景中重要不等式取等号的情形
四、一点看法
教育理念上说“不是教教材,而是用教材教”.从人教社教材的编排来看,是先得出数量关系(相等关系或不等关系),然后再用图形作补充说明.而我们的导入是先给出图形直观,然后再观察得到初步的结论,最后再进行严密的论证.这两种做法孰优孰劣,教师自有选择.现在教育取向的数学史日益引起广大一线教师的浓厚兴趣,我们想,如果能用信息技术把史料中闪烁智慧光芒的思想充分挖掘出来,而不是简单地复古,使课堂教学既有文化底蕴,又有现代信息社会的气息,那么教育取向的数学史将在信息技术的支持下大放异彩.这是我们的愿景.
1.代钦,李春兰.对中国数学教育的历史和发展之若干问题的理性思考——对张奠宙先生的访谈录 [J].数学教育学报,2012,(1):21-25.
