y=Asin(ωx+φ)+k——研究三角函数性质的法宝
2012-08-28湖北省襄阳市第五中学
中学数学杂志 2012年7期
☉湖北省襄阳市第五中学 谢 伟
三角函数是高中数学的重点内容之一,高中学生在分析三角函数问题时,往往因对三角变换的目标不明确、找不到解题方向而丢分.实际上,三角变换包括三个方面:①变换角,即化异角为同角;②变换函数名,也就是化异名函数为同名函数;③变换结构,主要是将高次式降幂为一次式,将低次式升幂为一次式.即将目标三角函数化为y=Asin(ωx+φ)+k的形式.因为课本中的三角函数的性质都是以y=Asin(ωx+φ)+k为对象进行讨论的,因此,我们只有将三角函数转化为这种模型,才能准确且方便地运用相关性质解题.
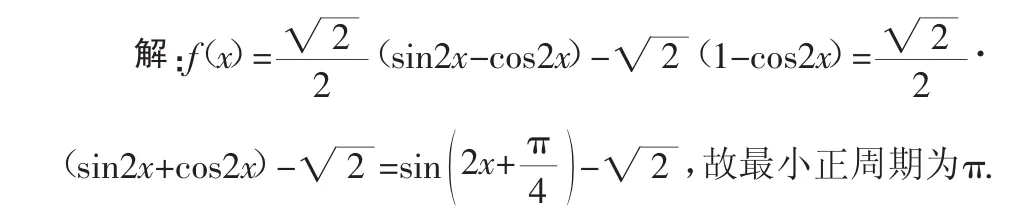
(1)求f(x)的最小正周期;
分析:求三角函数的最值,仍然离不开三角恒等变换,朝什么方向变形?怎样变形?这就要求熟练掌握三角函数恒等变形的方向和目标:转化为y=Asin(ωx+φ)+k型函数.结合目标,可以发现,首先需要变角,将变换为x,然后再变结构(降幂),将二次式结构化为一次式结构.

所以最小正周期为π.

分析:研究三角函数的性质常常需要通过等价变形将比较复杂的三角函数式转化为y=Asin(ωx+φ)+k型函数.再分析函数的图像变换、单调性、奇偶性等性质.
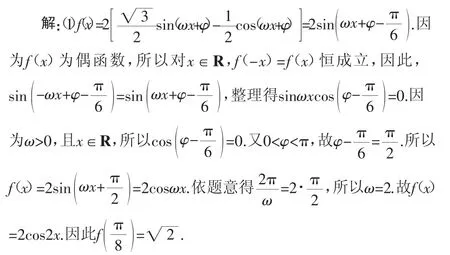

高中新课标教材是以y=Asin(ωx+φ)+k为对象研究三角函数的性质的,但是,高考试题为了考考生的化归与转化的能力,往往以比较复杂的三角函数形式来出现,这就需要我们在进行三角函数变换时牢固抓住三角变换的目标,即:将比较复杂的三角函数形式转化为y=Asin(ωx+φ)+k型函数.
