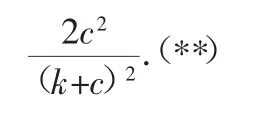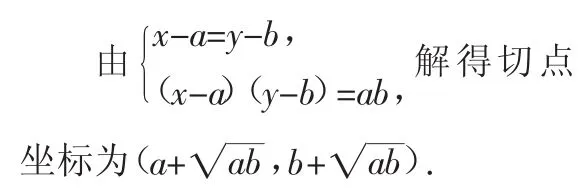巧构反比例函数图像探究函数最值型问题的新解法

☉上海市崇明中学 徐智愚（特级教师）

徐智愚，1964年12月出生，中学高级教师，上海市特级教师，上海市数学学科中学高级教师评审委员会成员，上海市普教系统数学名师培养基地导师.至今在《数学通报》等数学杂志上发表文章五十余篇.

有人问陈省身先生：“什么是数学？”陈省身先生回答说：“数学的对象是打‘引号’的数与形”.不少代数（函数）问题常有其几何的背景，若能予以充分揭示，利用其几何意义、图形性质，常能获得直观、独特、巧妙的新解法.

（1）当a=1、b=2时，求f（x）的最小值；

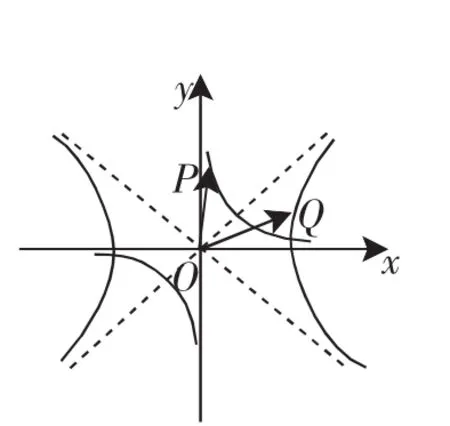
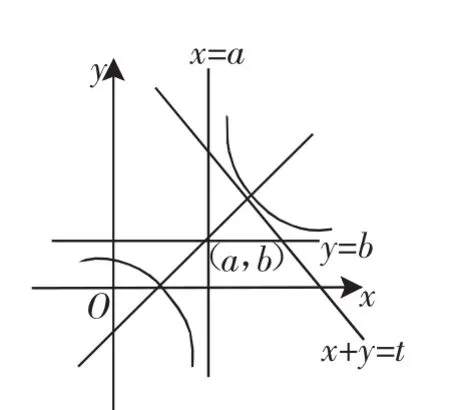
（2）若f（xa）≥2m-1对任意0

（3）设k、c>0，当a=k2、b=（k+c）2时，记f（x）=f1（x），当a=（k+c）2、b=（k+2c）2时，记f（x）=f2（x），求证

（2011年12月上海市七宝中学等十三校市重点中学高三数学联考压轴题）

标准答案很复杂，现仅将第三问的标准答案抄录如下.

图1

这时候，一些同学窃窃私语，一个同学问：“双曲线图像和反比例函数图像有什么关系呢？”不料此同学的提问引起了较多同学的共鸣，“一石”卷起“千重浪”，学生们分成各个小组，开始讨论此同学的问题，但是讨论的“焦点”已经集中在“双曲线图像和反比例函数图像的关系”这个问题的内核上.

图2

我很遗憾，因为我没有完成预定的教学计划；但我更高兴，因为我的学生的探究能力又有了新的提高！

在一次总复习课上，我布置学生做这样的练习.

我欣喜地发现，学生发现了较多我备课时没有发现的新方法，其中就包括巧构反比例函数图像解决此题的新解法！

图3

在另一节课上，当我向学生介绍了如下全国高考题的几种常规的方法后，几个同学到办公室找我，他们又发现了几个与我课上所讲不一样的解法，其中就有一个新的“数形结合”解法：巧妙构造反比例图像解之！我在课上及时进行了介绍，取得了很好的教学效果！

x>0，y>0，方程（*）的图像是反比例函数在第一象限内的部分（如图4）.

当直线x+y=t与双曲线右上支相切时，t即为所求最小值.由反比例函数图像的对称性知切点应在过中心（a，b）并与直线x+y=t相垂直的直线x-a=y-b上.

图4

顾泠沅先生曾经说：“当今，学生的独立分析和探究能力常常是被窒息的.虽然课程改革以来，我们鼓励学生探究，但是实际情况是被教师所替代.”

法国学者让·托马斯说：“教师的态度最终决定着革新的成败.”新课程改革是否顺利的关键取决于教师的教育观念的更新.因此，在高三复习课中，我们提倡把足够的时间留给学生思考；数学探究反对满堂灌，同时更反对机械重复学习，应该把足够的时间留给学生.我想：若教师平时上课时能经常注意“数形相融”，激发学生们的创造性“火花”，这对学生探究和创新能力的培养和提高是不无裨益的.

1.顾泠沅主编，邵光华著.《作为教育任务的数学思想方法》.上海，上海世纪出版股份有限公司，上海教育出版社，2009年.

2.郭海军.例谈反比例函数中的几个不变性问题.《中学数学》.2009，12.

3.王远征.与反比例函数的图像有关的面积问题.《中学数学》.2009，12.

4.徐智愚.思维破定势，反面更简捷，不用“数归法”——简析两道高三数列综合题的解法.《数学教学》.2008，7.

5.徐智愚.充分发挥课本例习题在探究性思维训练中的作用——新教材《行列式》教学扎记.《中学数学》.2008，4.