把握问题本质 探究通性通法

☉江苏省锡山高级中学 管恩臣

探究性教学是课堂教学的一种方式，其宗旨是让学生通过探索的方式解决问题，促进学生自主活动和积极思考，从而使学生的知识技能、兴趣和爱好得到和谐发展.采用这种教学方式的关键是选择好探究的问题，让学生多方寻求答案，解决疑问，并从中发现规律，把握问题本质，使探究活动富有意义.

一、问题设计的背景

图

苏教版数学5第一章复习题有这样一个问题：

如图1，已知A为定角，P、Q分别在A的两边上，PQ为定长.当P、Q处于什么位置时，△APQ的面积最大？

教材参考书提供了如下解法.

设A=α，PQ=a，AP=x，AQ=y，其中α、a为定值.

这个解法用到了重要不等式：x2+y2≥2xy，而关于不等式的知识要在数学5的第三章学习，显然用这个解法不现实.这又是一道非常好的题目，于是教师在本章复习课把它当做一个探究材料，与学生一起探索这道题目的解法，收到非常良好的效果.

二、教学实录和分析

1.解法探索.

例 如图1，已知A为定角，P、Q分别在A的两边上，PQ为定长.当P、Q处于什么位置时，△APQ的面积最大？

问题呈现给学生后，让学生探索5分钟.

教师：学生1以角为变量，根据正弦定理表示出两边，充分运用了已知一边及其对角这个条件.除了这个解法外，同学们还有没有其他解法？

教师：有没有同学帮助他解决这个问题？

学生3：由AP2+AQ2=（AP+AQ）2-2AP·AQ，可得PQ2=（AP+AQ）2-2AP·AQ（1+cosA），只要求AP+AQ的最大值就可以了，同学们感觉很有道理！

学生把a2+b2变形成（a+b）2-2ab这一想法很自然，不过对于本题不使用基本不等式来说，这样变形意义不大.

教师：AP+AQ的最大值怎么求呢？学生3说暂时没想好.

学生沉思了一会儿以后，学生4举手：AP2+AQ2=（AP-AQ）2+2AP·AQ，所以PQ2=（AP-AQ）2+2AP·AQ（1-cosA），只要求（APAQ）2的最小值就可以了，至此，该问题得以解决！

学生把a2+b2变形成（a-b）2+2ab这一想法就有很大跳跃性，之前较少接触！

教师点评：两种解法是从解三角形的基本方法正弦定理和余弦定理出发，努力构建目标函数，实践中学生运用解法1变形思路常规但运算烦琐，解法2运算简洁但技巧性强.两种解法出发点都非常自然，用到的知识是解三角形的核心知识，过程中的变形尤其是解法1中的变形是常用方法，充分说明例题是一道入口宽、意境深的好题！值得探索.

2.归纳本质.

变式：（2009福建高考理科）如图2，某市拟在长为8km的道路OP的一侧修建一条运动赛道，赛道的前一部分为曲线段OSM，该曲线段为函数y=Asinωx（A>0，ω>0，x∈［0，4］）的图像，且图像的最高点为；赛道的后一部分为折线段MNP，为保证参赛运动员的安全，限定∠MNP=120°.应如何设计，才能使折线段赛道MNP最长？

图2

学生很快得到两种解法.

解法1：在△MNP中，∠MNP=120°，MP=5.设∠PMN=θ，则0°<θ<60°.

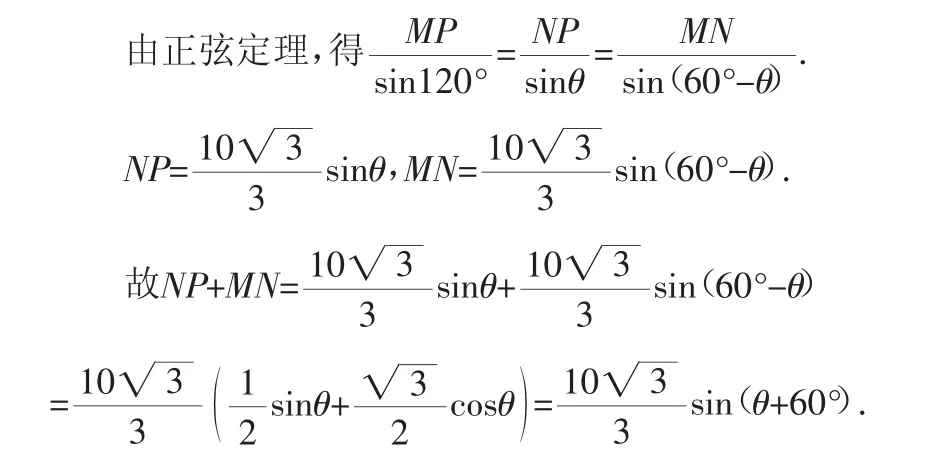
由0°<θ<60°，得当θ=30°时，折线段赛道MNP最长.

将∠PMN设计为30°时，折线段道MNP最长.

解法2：MP2=NM2+NP2-2NM·NPcos∠MNP，即25=NM2+NP2+NM·NP=（NM+NP）2-NM·NP，则只要求出NM·NP的最大值即可.

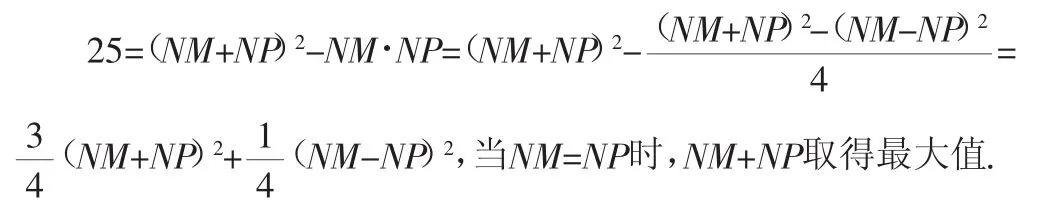
教师：例题和变式题中的（2）解法相似，这两个题目问题情景有什么共同特征？

学生：都是已知三角形的一条边及其对角.

教师：所求的问题本质上分别是什么？

学生：例题是求另两边积的最大值，变式题中的（2）求另两边和的最大值.

教师点评：这类问题的本质是：已知三角形的一条边及其对角求另两边积或和的最值问题，以另一角为变量，应用正弦定理，构建目标函数，是非常自然的想法；应用余弦定理也非常好，因为余弦定理a2=b2+c2-2bccosA可变形成a2=（b-c）2+2bc-2bccosA，这样余弦定理与两边和、两边差可以直接建立联系.

3.最值变化规律背景探索.

苏教版数学5第17页的第12题：如图3，已知圆内接四边形ABCD中，AB=2，BC=6，AD=CD=4，如何求四边形ABCD的面积？

学生上节课曾解过这个问题，现拓展：如图4，若A、B、D为定点条件不变，当点C在优弧BD上运动时，四边形ABCD面积何时最大？

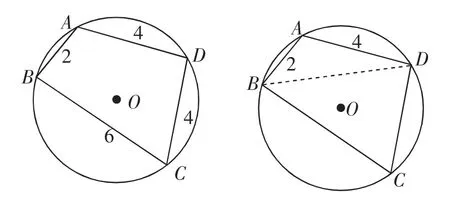
图3图4

学生5：连接BD，要使四边形ABCD面积最大，只要△BCD面积最大，而BD是定值，只要C到BD的距离CE最大即可，即CE过圆心时四边形ABCD面积最大.

教师：这个拓展问题和例题、变式题中的（2）有什么联系？

学生6：点C在优弧BD上运动时∠BCD大小不变，线段BD长度不变，同时所求最大值就是求CB·CD的最大值，和例题一样.

教师：对，同弧所对圆周角相等，所以保持∠BCD大小不变！除了学生的直观观察外，还能想到什么方法？

学生7：说出例题和变式题中的（2）的两种解法

教师：你能说出变式题中的（2）中点N的轨迹吗？学生8：根据题意应该是在一段劣弧上，如图5所示.教师：当角的顶点在圆上运动时，保持了角的大小不变，例题能否从这个角度来看呢？

学生9：可以假设线段PQ不动，点A在△APQ的外接圆上运动，这个过程中，A的大小保持不变，效果相当于点A不动线段PQ在动！如图6.此时，教室响起一阵掌声！

图5图6

三、教学设计的反思与感悟

本节课围绕已知三角形的一条边及其对角，求另两边积或和的最大值（同一时刻取得）的问题，放弃了教材参考书中的解法，从学生熟悉的正、余弦定理出发，师生、生生互动尝试、修正，一步步向目标前进，最终获得此类问题的两种解法，同时挖掘出几何规律！在这个过程中，教师要能够设计好探索的素材，把握好问题的本质，引导学生从不同的侧面和角度进行探索，设计中还应注意：

1.一题多解要重视通性通法.

一题多解是从不同的角度、不同的方位审视分析同一题中的数量关系，用不同解法求得相同结果的思维过程.教学中适当的一题多解，可以激发学生去发现和创造的强烈欲望，加深学生对所学知识的深刻理解，训练学生对数学思想和数学方法的娴熟运用，锻炼学生思维的广阔性、深刻性、灵活性和独创性，从而培养学生的思维品质，发展学生的创造性思维.

2.多题一解要抓住本质.

尽管数学习题浩如烟海头绪万千，但正如一切事物都有自己的规律一样，解数学题也有规律可循有方法可依，某些习题由于它们所反映的数量关系和空间形式存在相似之处，则可以串连起来考虑，提炼出共性，把握问题的本质，多题归一.为此，应该在学习中重视探索、自觉摸索解不同题目的规律，并依据这个规律去思考分析，不断丰富解题经验.长期坚持，遇到新问题就能思维活跃判断准确，有法可循，就能掌握多题一解的金钥匙.

3.立足教材灵活多变.

从近几年江苏高考题来看，把考查学生的能力和素质放在了首位的同时，也未忽视对基础知识、基本思想方法的考查，这些基本知识主要表现在课本例题和习题及其变形上.教师自己在平时的教学中要钻研教材，精心设计一题多解和一题多变的练习题，并能对相似的多题进行归纳，找出本质上的共性，多题一解，培养学生举一反三的能力，让学生在有趣的学习中探索知识，使他们灵活运用知识的技能、技巧得到提高.而在课堂上，师生互助，生生互助，共同努力，体验探索数学本质与规律的乐趣.