浅谈高中数学教学中如何培养学生解题反思

☉陕西省米脂县米脂中学 申婀娜

长期以来，高中学生陷入题海战术的泥沼中不能自拔，常常重复着昨日的错误，结果是老师苦恼，学生后悔.为什么会出现这样的状况呢？怎样改变这种状况呢？我陷入了沉思.

解题反思能促进学生的理解从一个水平升到更高的水平，促使他们从新的角度，多层次、多侧面地对问题及解决问题的思维过程进行全面的考查、分析与思考，从而深化对问题的理解，揭示问题的本质，探索一般规律，并进而产生新的发现，同时也有助于优化学生的思维品质，提升学生的数学能力.

那么如何培养学生进行解题反思呢？如何使之成为学习的好习惯呢？

一、反思错解，探究解题过程的合理性

例1 已知x、y≥0，2x2-3xy-y2+8x+3y-4z+2=0，2x+y-6=0.求z的取值范围.

错解：由题意得y=6-2x. ①

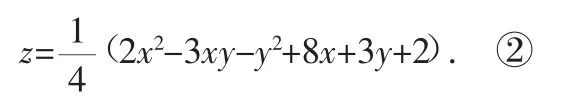
把①代入②，整理得z=（x+1）2-5.

因为x≥0，所以x=0时，zmin=-4.

所以z∈［-4，+∞）.

反思：上述解法虽然注意了x≥0，但忽视了隐含条件y对x的约束：y=6-2x≥0.结合x≥0知x∈［0，3］，所以z∈［-4，11］.解完一道题后，应进一步思考：题目中所有条件都用过了吗（包括括号内的条件）？题目所要求的问题解决了吗？还有没有需要增加说明和舍掉的部分？

二、思一题多解，探究优化解法

很多数学问题有多种解法，解题后要多角度思考，看是否还有其他解法，通过寻求新的方法，可以开拓思路，防止思维定势，及时总结出各类解题技巧，养成“从优”、“从快”的解题方式.

三、反思解题的思维过程，培养思维的灵活性

解题的关键是从已知和未知中寻找解题途径，学生在做完一道题后的反思，不仅是简单回顾或检验，而应根据题目的基本特征与特殊因素，进行多角度、多方位的观察、联想.反思自己的解答是否有错，错误的原因是什么.若解答正确，则想一想有无新的解题途径.若有另解则应分析比较，找出最佳解法，最后再总结一下解答此类题目有无规律可循，使学生思维的灵活性在变换和化归的训练中得到培养和发展.

例3 已知关于x的三次方程x3-mx2-2mx+m2-1=0有且仅有一个实根，求实数m的取值范围.

对于此题，很多学生在练习时，没有清晰的思路，一开始就从关于x的方程仅有一个实根去考虑，但发现行难以解决问题.于是在点评时，鼓励大家反思题目已知及所求目标的特征，既然从字母x入手有困难，何不以字母m为主元试试看？学生受到启发：关于字母x是一个三次方程，而关于字母m则是一个二次方程.基础较好的学生马上领悟过来，将原方程变形得：m2-（x2+2x）m+x3-1=0，解得m=x-1或m=x2+x+1.考虑到有唯一实数解，则

四、思形似质不同题目，提高辨别能力

①不等式的解集为［0，3）；

②不等式在［0，3）上有解；

③不等式在［0，3）上恒成立；

④不等式的解集是区间［0，3）的子集.

反思：上述四个小题常容易混淆，通过反思各种解决方法的不同，弄清四个不同的概念及相应的解题方案.

在数学解题中，教给学生解题后再分析、再思考的方法，培养学生多思善想的良好习惯，通过对解答的辨析和反思，对解法的深化、变式，不仅给学生更广阔的思考空间，有利于知识的归纳、规律的形成，促进“双基”的掌握，而且能优化学生的数学认知结构，培养了学生高层数学思维的能力和创新能力，加强知识的同化和有效迁移，促进知识向能力转化，使学生“乐学”、“会学”，是提高解题能力的重要途径，也是提高数学教学质量的有效途径.