创造性使用高中数学教材的主要策略

☉江苏省常州市第一中学 王月维

创造性使用教材，要求教师在充分了解和把握课程标准、学科特点、教学目标，并仔细研读和分析教材的基础上，立足于学生的学习需要，以教材为依托，根据学生的实际情况并结合具体的教学环境，利用现有的教学资源，充分发挥教师的个人教学特长和创新能力，有计划、有目的地对教材进行活化、改编和重构，并灵活有效地组织教学，从而拓展教学空间，促进学生的主动发展的过程.它也是教师个性化地运用教材内容，生成实际的教学内容的一种现代教学策略.

一、深挖教材

挖掘教科书的教学内容，站在学生发展的高度，旨在拓宽学生的视野，锻炼学生的思维，培养学生分析问题、解决问题的能力，而不是刻意加深教科书深度，加重学生负担，更不是以卖弄“学识”为目的，讲一些偏、难的内容和古怪、烦琐的习题.

案例：数列的概念（必修5第2章2.1）

《数列》内容，在高中数学中起着承前启后的作用，有关于“数列是一种特殊的函数”这一问题，以往的做法是在第一课时不提或者一带而过.但我们仔细研究教材，可以发现在这一节明确提到了这一问题.在教材中有这样一段话：“在数列{an}中，对于每一个正整数n，都有一个an与之对应，因此，数列可以看成以正整数集N*（或它的有限子集）为定义域的函数an=f（n）.反过来，对于函数y=f（x），若f（i）（i=1、2、3、…）有意义，那么我们可以得到一个数列f（1），f（2），f（3），…，f（n），…”.鉴于教材的这种处理，教师应该意识到“用函数思想研究数列问题”是在学习数列的一开始就渗透在教学中的，教学中可以紧扣这一中心，自然“生成”数列的概念、表示法等问题.

二、改编教材

教材的改编的内涵很丰富，可以改编情境（情境的选择既切合学生的生活，又能够激发学生的学习兴趣，关键是还要与所讲的知识点联系紧密，反映全面）；可以改编例题（例题的选择要能反映学生所得，也要能为后期的教学做好铺垫）；可以改编习题（命制试题的主渠道就是“改编教材上的题目”）等，不一而足.

案例：算法的含义（必修3第1章1.1）

例1 给出求1+2+3+4+5的一个算法.

学生可能很快给出算法步骤，但会觉得没有思考价值.如果在开发过程中，加入变化，就能激起所有学生的兴趣，也能体现算法的作用.设计如下.

变式1：给出求1+2+3+....+100的一个算法.

学生对于此题，肯定会给出书本的算法2，但是能否再进一步，这是教师对于教材和学生开发最有效的组合，也是最实际的开发.

这个题就能激发学生的兴趣，教师不见得要在课堂上解决这个题，但是告诉学生学完后续内容，就能解决这个问题，相信学生都迫不及待地希望听下一节课.

三、增补教材

这里所讲的增补教材，并不是将新教材中没有涉及的老教材的内容一股脑儿地补充给学生，以不变应万变，而是指针对新教材中“有关结论不全面，易引起学生的误解，造成人为的学习障碍”的内容进行适当地增补以完善.

案例：函数的零点（必修1第2章2.5.1）

函数的零点将几何问题和代数问题结合在了一起，充分体现了数形结合思想.研究教材后发现：用二次函数引入缺乏吸引力；结论的给出过于直接，缺少问题铺垫；零点存在的结论易使学生有错误认识等.可以如下设计.

引入时：方程lnx+x－4=0是否有实根？如果有，有几个？在哪里？（用陌生的有挑战性的问题引起学生的思考，激发学习兴趣）

零点存在性定理的给出可通过设计以下“问题串”：①为什么会在函数前加“不间断”这个修饰语？②［a，b］变化为（a，b），为什么？③结论是有零点，那么有几个呢？④若f（a）·f（b）>0，是不是表示没有零点？

学生已有的认知结构是学生知识的生长点，也是教师开展教学活动的起点.问题的解决就是由未知向已知的迁移，再回到未知的过程.

四、整合教材、重组调整顺序产生的问题

许多高中是按照1-4-5-2-3的顺序进行教学，这在使用新教材的同时也顾及到原有教材中的线性逻辑顺序，也更符合学生的认知规律.这样处理的话，在一些定理、公式给出时，就不必完全按照教材上的方法，而可以根据学生学过的、相关的知识进行重组、融合，形成全面的、综合性的背景素材.在“温故知新”的情境中，通过对比、联想来学习新的知识，在优化认知结构的同时，丰富他们的创造力，锻炼他们的理解能力.

五、探究性教材的使用

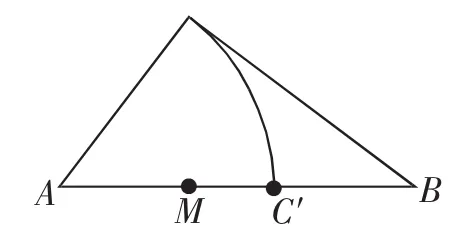
图1

作为教材内容的补充，苏教版的《数学》有很多探究性的内容，它所选取的内容既拓展了学生的视野，又为学有余力的学生提供了一个更为广阔的学习空间，同时还为教师创造性使用教材提供了可以选择的方向，有利于形成更好的教学设计.

案例：几何概型悖论（必修3第3章3.3）.

几何概型的教学目标是了解几何概型的基本特点并会进行简单的几何概率的计算.3.3中的

例3：“在等腰直角三角形ABC中，在斜边AB上任取一点M，求AM

图2

习题3.3中的第6题：“在等腰直角三角形ABC中，过直角顶点C在∠ACB内部任作一条射线CM与线段AB交于点M，求AM

在教学中，这一现象势必引起学生的认知困惑.教师可以利用这一契机，适当介绍概率悖论，如著名的贝特朗问题，激发学生的探索与思考.

对教材进行创造性开发，需要教师不断学习、提高，其能力也不是一朝一夕可以形成的，只有在实践中不断潜心学习，大胆实践，认真反思，并且不要拘泥于固定环节、固定课型的创造性使用.创造性使用教材并非仅仅限定在新授课里，更不是仅仅局限于情境引入的环节.在练习课、复习课中，在任何一节课的任意一个环节中，我们都可以通过独具匠心的个性化设计，通过不断积累经验，改进不足，形成具有个人特色的创造性使用教材的方法.