一道2011高考题的解法探 究与推 广

☉江苏省常熟中学 朱峰

题目 （2011年重庆高考理科卷第7题）设a>0，b>0，若a+b=2，则的最小值为（ ）.

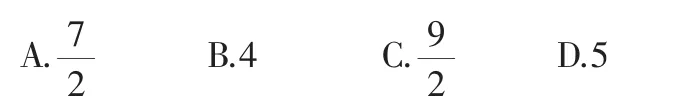
这道试题从它的问题背景和难易程度来看，显然相当平凡，不见得有多大的“新奇”之处，但剖析其内涵，挖掘其内在的功能，可引发众多的思考，笔者结合自己的教学实践，谈谈试题给我们的思考，供大家参考.

“问题是数学的心脏”，学习数学的过程与解题紧密联系的，而数学能力的提高在于解题的质量而不是解题的数量.所以要重在研究解题的方向和策略.要善于从题目的条件和求解（求证）的过程中提取有用的信息，作用于记忆系统中的数学认知结构，提取相关的知识，推动题目信息的延伸，归结到某个确定的数学关系，从而形成一个解题的行动序列，这就是解题方向.题目信息与不同数学知识的结合，可能会形成多个解题方向.

一、代换

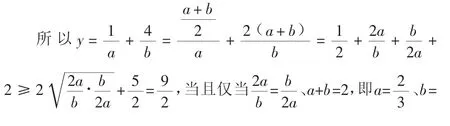
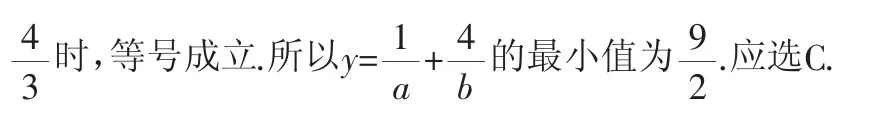
二、构造

点评：巧妙地构造定必分点坐标公式，引入参数λ，再利用基本不等式求解.

三、转化凑项

点评：将变量x转化成y，进行凑项，使积为定值，利用基本不等式求解.

四、三角换元

点评：根据已知条件，通过三角恒等变形，创造基本不等式成立的条件，从而进行解题.

五、引入参数（加0法）

点评：引入参数m，巧妙地构造基本不等式进行求解.

六、构造一元二次方程，利用根的判别式

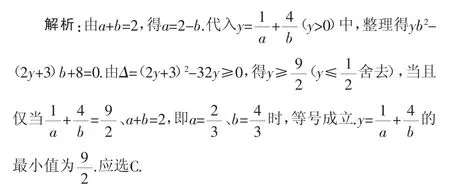
点评：巧妙地构造关于b的一元二次方程，由根的判别式求解.

七、利用平均数代换，构造方程

点评：利用平均数代换，转化成关于t的方程，利用根的判别式进行求解.

反思是对所解的数学问题进行发散性扩展或是收敛性的概括.发散性扩展是指改变习题条件、扩大外延的一题多变的思考，培养发散性思维；而收敛性的概括则是对所解的题目从结构上和思路上进行抽象、概括和归纳，以便形成更高层次上的题型模式和数学思维模式.因此，要求教师对习题、试题进行“深加工”，重视对其的挖掘、引申和改编，进行创造性的设计.

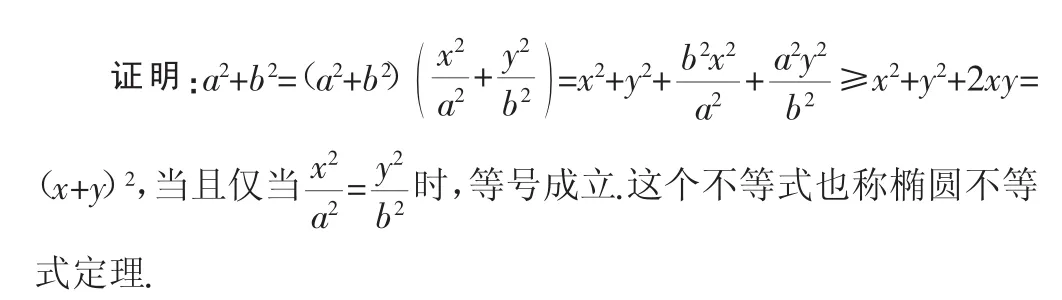
应用某些习题的结论和拓广所得的新知识解决问题，不仅能使知识深化，而且也有可能使解题方法巧妙、简捷，从而使学生体会创造的美感，激发学生的创造热情，培养自觉、自主的创造品质.

1.求二元一次式的最值.

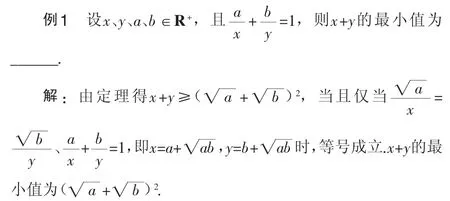
2.求二元二次式的最值.

例2 已知x、y满足x2+y2-2x+4y=0，求x-2y的最值.

4.求二元分式函数的最值.

在数学教学中，若老师有目的、有意识地引导学生研究一些典型习题、考题，揭示其丰富的内涵，则不仅有利于学生掌握基础知识，而且对于培养应变能力、开拓思路、活跃思维都是有益的.