基于跟踪微分器的模型参考自适应控制

周 涛， 王 磊

(1.洛阳师范学院物理与电子信息系，河南 洛阳 471022; 2.同济大学中德学院，上海 200092)

0 引言

自适应控制的研究始于20世纪50年代，用来解决高性能飞机自动驾驶仪的设计问题，这类飞机的飞行高度和速度变化范围很大，从而造成大幅度的参数变化［1］。许多动力系统数学模型参数在较大的范围内具有不确定性，而自适应控制可以补偿系统参数的不确定性，因此它在许多实际问题中得到应用，例如电力系统、电机控制、机器手的控制、飞行器控制、化工过程和舰船的驾驶等［2］。目前，自适应控制主要有两种形式:一种是模型参考自适应控制方法(MRAC);另一种是自校正方法(STC)。文献［3］采用输入—输出变量设计了超声波电机模型参考自适应转速控制器，并给出了自适应速率在线调节等方法以改善起始阶段的转速控制性能;文献［4］运用分散模型参考自适应控制方法研究了一类不确定时滞大系统问题，在选择参考模型时，根据系统所期望的性能指标，考虑各子系统的相互作用;文献［5］针对模型参考自适应控制中参考模型的建立问题，探讨了3种模型设计方法;文献［6］提出了自适应反推控制应用于具有不确定参数的永磁同步电机速度跟踪控制，该方法能够在系统参数发生变化时保证控制系统的快速跟踪性等［7］。

本文提出了一种基于跟踪微分器的二阶系统模型参考自适应控制。首先，证明了该模型参考自适应控制系统的全局稳定性，并推导了参数自适应调节律表达式;然后，说明了基于跟踪微分器的模型参考自适应控制系统的结构;最后，在雷达伺服系统中进行了试验验证，证明了该新型控制器的有效性。

1 二阶系统模型参考自适应控制的设计

1.1 二阶系统误差状态方程

设二阶系统被控对象为［8］

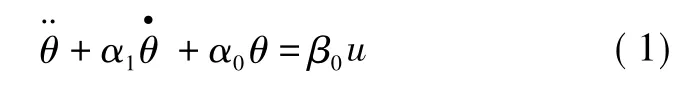
式中:θ为系统输出;u 为控制输入;α0≥0;α1≥0;β0＞0。定义参考模型为

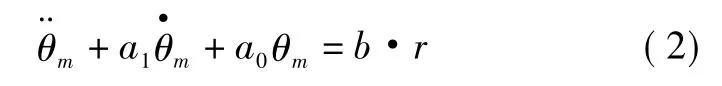
式中:θm为参考模型的输出;r为系统指令输入;a0＞0;a1＞0;b＞0。

定义误差信号为

由式(2)减去式(1)可得误差动态方程为

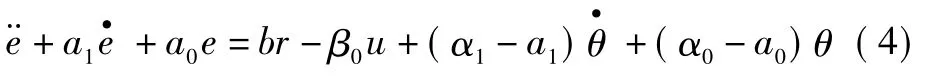
设计自适应控制律为

将式(5)代入式(4)得

式(7)中，s为标量函数。因为矩阵A的特征值具有负实部，所以系统(7)是稳定的，存在正定对称矩阵P、Q使得

1.2 模型参考自适应控制的稳定性

取李雅普诺夫函数

式中，λ ＞0。

xTPx的导数为

式中，xTPBβ0ΦTV，β0VΦBTPx均为标量函数，且 P 为正定对称矩阵，所以

由引理可知［2］，向量Φ的自适应律取为

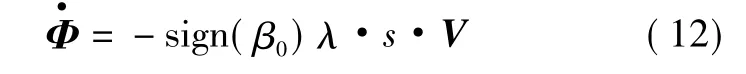
式中，sign(β0)为符号函数。均为标量函数，

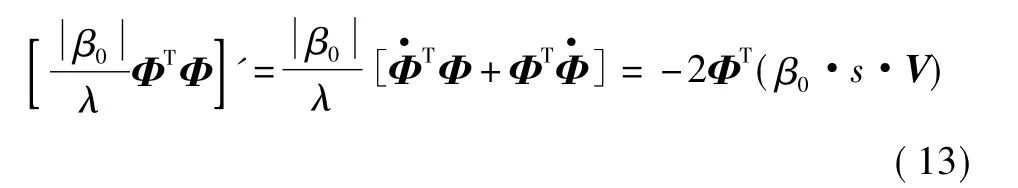
由式(7)～式(8)、式(11)和式(13)得(推导过程略)

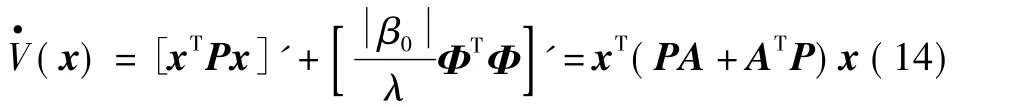
由式(8)、式(14)得

由李雅普诺夫主稳定性定理知，系统(7)为全局渐近稳定。

1.3 参数自适用调节律的设计

因为

2 基于跟踪微分器的二阶系统模型参考自适应控制

由式(5)的自适应控制律和式(17)的参数自适应调节律可知，为了实现自适应控制，需要得到被控对象的输出信号θ和输出的微分信号，以及误差信号e和误差的微分信号实际系统输出信号和误差信号一般都包含大量高频噪声成分，常规的微分算法会造成严重的高频噪声放大效应，影响控制效果和精度，因此输出的微分信号及误差的微分信号常常难以利用。理想微分信号的获取一直是控制工程上一个难点，这里，在模型参考自适应控制中，提出采用二阶非线性跟踪微分器(Tracking Differentiator，TD)得到输出的跟踪信号和理想的微分信号，而且很好地抑制了高频噪声放大效应［9］。

2.1 二阶最速离散跟踪微分器

二阶跟踪微分器可以对它的输入信号进行低通滤波，同时得到输入信号理想的微分信号。设h为采样周期，x1(k)，x2(k)为二阶系统的状态变量，二阶最速离散跟踪微分器为［9］

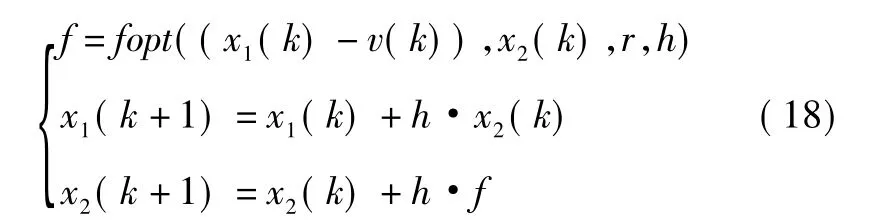
二阶最速控制函数 fopt(x1(k)，x2(k)，r，h)为［10］

式中:fix(b1)为向零取整函数;sat(x，n)为饱和函数。

2.2 基于跟踪微分器的模型参考自适应控制系统

基于跟踪微分器的二阶系统模型参考自适应控制系统结构如图1所示。

图1 基于跟踪微分器的二阶系统模型参考自适应控制系统结构图Fig.1 Structure diagram of model reference adaptive control based on tracking differentiators

图1 中:r(t)为控制系统的指令输入信号;θm(t)为参考模型的输出信号;θ(t)为被控对象的输出信号;u(t)为被控对象的控制输入信号;e(t)=θm(t)－θ(t)为误差信号。图1中包含了两个二阶最速离散跟踪微分器:跟踪微分器1能对实际输出信号进行低通滤波，并获得输出信号的跟踪值θ和微分信号;跟踪微分器2能对误差信号e(t)进行低通滤波，得到误差信号的跟踪值e和微分信号

3 实验验证

在某型雷达系统进行实验验证，利用工控机系统作为控制平台，该雷达系统如图2所示。

图2 实验的雷达系统Fig.2 Experimental radar system

该雷达伺服系统被控对象为［8，11］

对比式(1)可得:α0=35，α1=30，β0=120。

参考模型为

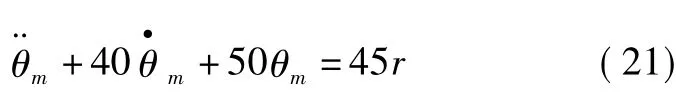
当设定输入指令为正弦信号时，被控对象的位置跟踪误差如图3所示(纵坐标的单位为(°))，控制器参数h0、h1、h2的自适应变化曲线如图4所示。

图3 正弦信号位置跟踪误差Fig.3 Sine signal position tracking error

图4 控制器参数的变化曲线Fig.4 Change curves of controller parameters

图3 表明在2.5 s之后被控对象正弦信号的跟踪误差始终小于 ±0.4°×10－3。同时，图4表明，由于正弦信号属于持续激励信号，导致了快速的参数收敛。

假设雷达伺服系统被控对象变为

即 α0=0，α1=5，β0=70。

参考模型仍为式(21)，且两个TD的参数、模型参考自适应控制器的初始状态、自适应调节律参数λ和正定矩阵Q取值均保持不变。设定输入指令为相同的正弦信号，则被控对象的位置跟踪误差如图5所示(纵坐标的单位为(°))，控制器参数的自适应变化曲线如图6所示。

图5 正弦信号位置跟踪误差Fig.5 Sine signal position tracking error

图6 控制器参数的变化曲线Fig.6 Change curves of controller parameters

图5 表明在2.5 s之后被控对象正弦信号的跟踪误差仍小于±0.4°×10－3，图6表明自适应控制器的参数快速达到收敛。当雷达伺服系统被控对象模型的参数α0、α1和β0在较大范围内变化时，实验表明采用该新型控制器的伺服系统总能够保持高的位置跟踪精度。

4 结论

本文提出的新型二阶系统模型参考自适应控制利用跟踪微分器获取理想的微分信号，同时跟踪微分器对输出信号和误差信号进行低通滤波。实验结果表明，当雷达伺服系统的数学模型参数发生了较大变化时，该控制器能自动补偿伺服系统参数的不确定性，提高了系统稳态和动态跟踪精度，对处理一般二阶系统模型参数的不确定性具有重要的参考意义和应用价值。

［1］ 贺昱曜，闫茂德.非线性控制理论及应用［M］.西安:西安电子科技大学出版社，2007.

［2］ SLONTINE J J E，LI Weiping.应用非线性控制［M］.程代展，译.北京:机械工业出版社，2006.

［3］ 史敬灼，张慧敏.行波超声波电机Lyapunov模型参考自适应转速控制［J］.电工技术学报，2011，26(4):44-49.

［4］ 翟丁，金超，梁力，等.一类不确定时滞大系统的分散模型参考自适应控制［J］.东北大学学报，2011，32(2):169-171.

［5］ 刘少华，段征宇.飞行器自适应控制参考模型建立方法研究［J］.飞行力学，2011，29(4):56-59.

［6］ 刘栋良，王家军，崔丽丽.永磁同步电机参数自适应调速控制［J］.电工技术学报，2011，26(8):159-164.

［7］ 魏春玲，王强德，孔宪福.不确定高次随机非线性系统的自适应控制［J］.控制理论与应用，2011，28(2):242-246.

［8］ 刘金琨.先进PID控制MATALAB仿真［M］.北京:电子工业出版社，2004.

［9］ 韩京清.自抗扰控制技术—估计补偿不确定因素的控制技术［M］.北京:国防工业出版社，2008.

［10］ 孙彪，孙秀霞.离散系统最速控制综合函数［J］.控制与决策，2010，25(3):473-477.

［11］ 高磊，许人灿，陈曾平.一种宽带单脉冲雷达测角方法［J］.电光与控制，2011，18(10):55-58.

［12］ 李莉，孙富春，裴卫东.基于模糊奇异摄动模型的直接型自适应控制器的设计［J］.电光与控制，2011，18(11):62-66.