基于STL快速重构平面有限元网格边界

王家林，张德立，何 琳

(重庆交通大学土木建筑学院，重庆400074)

在有限元分析中，有时需要找出模型的边界进行某些特殊的处理，如对于多连通截面的扭转问题，需要在外边界上施加应力函数为零的约束条件，在内边界上施加应力函数相等的约束条件［1］。如果基于几何来建立有限元网格，则边界是预先已知的;如果直接从其它有限元软件中导入网格数据，则边界需要根据网格数据分析得到。所以，快速、高效率地根据有限元网格数据找出模型边界成为算法优化的一部分。

笔者针对多连通截面的平面有限元网格，灵活应用C++标准模板库(简称 STL)中的 vector、list、set和map容器，研究了快速分析模型边界的方法，并成功地应用于多连通截面扭转问题的有限元分析中。

1 C++STL中基本容器的特点

C++标准模板库STL是C++的组成部分，提供了大量的可复用软件组件，包含了vector、list、set、map等容器及算法，其实现速度和内存利用方面都是高效的［2］。充分利用STL技术能够极大地提高应用程序的开发效率，殷际英［3］将STL技术用于边界元程序设计中，解决大量数据的动态存储和内存分配问题;李余江，等［4］运用STL技术以向量模板类的特化继承对象为变容量数据容器编制了面向对象的有限元程序;唐丽玉，等［5］和吴小平，等［6］将 STL 技术用于Delaunay三角形网格的高效构建。

vector是一种连续存放、可根据序号随机访问数据元素的容器，在所有容器中具有最高的元素访问效率。不过在插入和删除元素时会产生内存块的拷贝，当内存空间不够时，需要重新申请一块足够大的内存并进行内存的拷贝，导致执行时间增加。

list是STL提供的双向链表，它的数据元素在内存空间不必连续存放，插入和删除数据元素的效率高。list数据结构只具有顺序访问数据元素的能力，不能通过序号直接访问一个指定的数据元素。

set容器使用一种称为红黑树的平衡二叉检索树结构来组织泛化的元素数据，其每个节点包含一个取值红色或黑色的颜色域来进行树的平衡处理，不会将重复的键值插入容器，也不需要指定具体的插入位置，而按元素在树中的关联关系，进行位置检索和插入，元素的删除亦然。元素数据的检索，使用的是二叉检索树的中序遍历算法，检索的效率高于vector、deque 和 list等容器。

map映照容器由一个键值和其它若干数据(映照数据)组成，键值和映照数据之间，可建立一个数学上的映照关系。容器的数据结构同样是采用红黑树进行管理，插入的元素键值不允许重复，所使用的节点元素的比较函数，只对于元素的键值进行比较，元素的各项数据可通过键值检索出来。故它能快速查找、插入、删除元素。

2 网格边界的分析方法

2.1 单元节点编号的存储方式

对于一个确定的有限元网格，单元个数及每类单元的节点个数是已知的，因此为了提高数据访问效率，对于每个单元采用了vector＜int＞数据类型存储各节点编号。

2.2 边界的判别方法

在平面有限元网格中，一条边如果只在一个单元中出现，则该边为边界上的边，一条边如果被两个单元共有则不是边界。例如，对于简单网格(图1)，只属于单元1的边(2 7 4)是边界。既属于单元1又属于单元2的边(4 8 5)就不是边界。

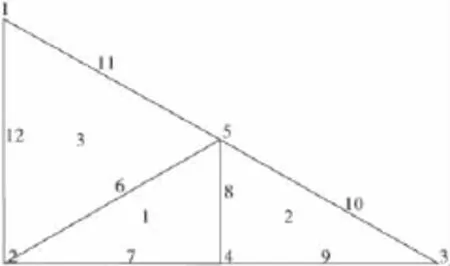
图1 平面有限元网格示例Fig.1 Plane finite element mesh

2.3 利用set容器分析边界

在查找模型边界的过程中，约定单元的每个边采用该边上节点编号按逆时针方向组成的字符串表示。例如，对于图1的平面有限元网格，单元1的边为“2 7 4”、“4 8 5”和“5 6 2”，单元2的边为“4 9 3”、“3 10 5”和“5 8 4”。很显然，不在模型边界上的边会以相反的节点顺序出现两次，如单元1的边“4 8 5”和单元2的边“5 8 4”。于是，可以采用下面步骤来实现边界的快速识别:

1)建立一个存储字符串的set，用以保存分析过程中识别出来的边界。

2)对于单元的每一个边，按单元顺时针方向将边上的节点编号组成字符串，用该字符串在set中查找有无该字符串:①如果在set中找到该字符串，说明此字符串表示的边为第2次出现，不是模型边界，则从set中将该字符串删除;②如果在set中找不到该字符串，表明此字符串表示的边为第1次出现，可能是模型边界，则将该边上的节点的编号按单元逆时针方向组成字符串后加入set中。

3)当全部单元的所用边均按照步骤2)分析处理完毕后，则set中的字符串标记出的边为模型的边界。

按照上述算法，set中不是模型边界的边能够及时从set中删除，使set容器中的元素个数尽可能少，从而提高查询效率。

2.4 利用map容器分析边界环线

尽管set容器中的字符串标记了模型的边界，但各个边处于散乱状态，没有连接成边界环线，扭转分析需要能识别出每一个边界环线。在图1中，处于单元1的边界(2 7 4)和处于单元2中的边界(4 9 3)是相连接的。可见两条相连的边界，其中一条的末尾节点号正好是另一条的首节点号。基于此特点，即可建立形成边界环线的算法。

2.4.1 生成边界map

从前述set中取出各边界边组成的字符串，以首节点号为关键字、字符串为数据形成map，具体算法步骤为:

1)建立一个以整数为键值，数据为字符串的map。

2)按顺次遍历的方式访问set中的每个元素(即表示每个边的字符串)，获得第1个节点编号，以第1个节点编号为键值、以字符串为映照数据生成一个元素添加到map中。例如，对于单元2中的边(3 10 5)，在 set存放为字符串“3 10 5”，就以“3”为键值、“3 10 5”为映照数据插入map中。

对set中每个元素执行完毕后，map中每个元素的键值表示了一个边的起始节点，其数据字符串表明了该边上的各个节点。

3)清空set容器以节省内存。

2.4.2 利用边的连接性生成边界环线

基于map中边的连接性即可形成各条边界环线，具体算法步骤为:

1)新增一个list＜int＞类型的链表表示一个环线，用于存放一个环线上的各个节点的编号。

2)从map中取出第一个元素(即获得该元素的数据字符串，并从map中将该元素删除)作为当前分析边。

3)从当前分析边的字符串中取得各个节点编号，除最后一个节点外，将其余节点的编号顺次加入到环线链表中。不加入最后一个节点是为了避免环线上节点编号重复，例如:对于图1中的边界“2 7 4”，将边界存入环线时只存放节点号2、7。

4)当前分析边的最后一个节点的编号指出了与之相连的下一个边的起始节点，因此以其作为键值在map中查找相连边:①如果在map中找到了与当前分析边相连的下一边，则将该边从map中取出(即获得该元素的数据字符串，并从map中将该元素删除)作为新的分析边，回到步骤3);②如果在map中找不到相连的边，则表明环线已闭合，保存当前边界环线。

5)查看map中是否还有未分析边:①如果map非空，则表明边界环线还没有分析完毕，回到步骤1);②如果map已空，则表明边界环线已经分析完毕，结束边界环线的分析。

上述算法中，从map中逐步取出边的措施及时删除了已经分析过的边，使map中元素个数递减，此策略有助于提高map中元素的查找效率。

3 算法示例

用ABAQUS有限元软件建立一个含两个孔洞的平面区域，采用三角形单元进行网格划分后得到如图2的有限元网格，写入inp文件。

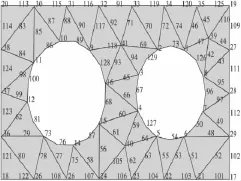
图2 ABAQUS划分的平面有限元网格Fig.2 Finite element mesh in ABAQUS

ABAQUS的inp文件是关于有限元模型的文本文件，文献［7-8］对其具体信息进行了介绍。笔者编写了从inp文件读取到网格数据并分析边界的程序，找出了网格边界并连成了环线，其结果如下:

与图2对比可见，成功地获得了图中网格的3条边界，验证了前述算法的正确性。

4 结语

本文方法利用了set和map容器能够快速查找数据的特点，能达到快速、高效地从网格中找出边界并将边界连成环线。程序量小、简单、适用，解决了基于平面有限元网格快速分析模型边界的问题。

［1］ 崔振山，刘国燕，刘才.多连通任意截面杆件扭转问题的有限元法［J］.燕山大学学报，2001，25(4):297-300.

Chui Zhenshan，Liu Guoyan，Liu Cai.Finite element method for torsional bar with arbitrary shaped and multiple-connected crosssections［J］.Journal of Yanshan University，2001，25(4):297-300.

［2］ 叶至军.C++STL开发技术导引［M］.北京:人民邮电出版社，2007.

［3］ 殷际英.STL技术在边界元离散化过程中的运用［J］.北方工业大学学报，2001(1):64-67.

Yin Jiying.Application of STL technique to discretion by boundary element method［J］.Journal of North China University of Technology，2001(1):64-67.

［4］ 李余江，殷际英，赖锡煌，STL技术在面向对象有限元程序中的应用［J］.应用力学学报，2005，22(1):146-149，170.

Li Yujiang，Yin Jiying，Lai Xihuang.STL C++in finite element programming with applications［J］.Chinese Journal of Applied Mechanics，2005，22(1):146-149，170.

［5］ 唐丽玉，朱泉锋，石松.基于STL的Delaunay TIN构建的研究与实现［J］.遥感技术与应用，2005(3):40-43.

Tang Liyu，Zhu Quanfeng，Shi Song.Research and implementation of constructing delaunay TIN based on STL［J］.Remote Sensing Technology and Application，2005(3):40-43.

［6］ 吴小平，许天会，赵文光.高效构建Delaunay三角网算法研究及应用解决方案［J］.水电能源科学，2009(1):96-98，108.

Wu Xiaoping，Xu Tianhui，Zhao Wenguang.Research on effective construction of delaunay TIN algorithm and its solution［J］.Water Resources and Power，2009(1):96-98，108.

［7］ 庄茁.基于ABAQUS的有限元分析和应用［M］.北京:清华大学出版社，2009.

［8］ 刘展.ABAQUS6.6基础教程与实例详解［M］.北京:水利水电出版社，2008.