变截面开口薄壁钢箱稳定性分析

刘芳平，周建庭

(1.重庆交通大学土木建筑学院，重庆400074;2.重庆三峡学院 土木工程学院，重庆404000)

任何薄壁结构事实上都是由壳体构件组合而成，如果用壳体理论分析薄壁结构，结果比较精确，但工作量非常大，对于一些由多个此类结构组成的体系，壳体理论的分析就变得艰难。此时，就能够利用薄壁构件长度方向比横截面要大的特点，引入一些适当的假定，把它作为一根构件进行研究，也能够得到精确的结果。假想荷载法(Notional Load Technique)作为推导薄壁构件稳定理论的一种有效方法，由 Vlasov［1］首先提出，并被广泛采用［2-3］。但是，目前的假想荷载法不是全面的。存在的问题是:没有在板件理论的范畴内确定假想荷载，因而在薄壁截面的板件内存在剪应力和横向正应力时，目前假想荷载法不能得到正确的平衡微分方程。

1 开口薄壁构件弯扭分析基本假定

Vlasov［1］提出的开口截面构件基本假设如下:

1)刚周边假定。在构件逐步变形的过程中，其横截面形状始终不变。即，各横截面有可能产生垂直于截面的翘曲，但在自身平面内的投影保持固定形状，只是像刚性盘子一样转动或者是进行移动。

2)构件中面内剪应变为0。也就是说，弯曲扭转产生的中面内剪应变对构件内应力分布影响非常小。

笔者从薄板理论出发，用假想荷载法利用单块板的平衡推导了薄壁构件的平衡微分方程。在推导弯扭平衡微分方程时，除了上面的两条基本假定之外，补充了以下假定:

3)材料为理想弹性各向同性均质材料。

4)小变形分析。

5)假定薄壁构件由平板组成。

2 开口薄壁构件弯扭平衡微分方程

2.1 薄板单元体的假象荷载

假想荷载实际上不是真正的外荷载，因为它的作用与荷载一样，能够促使板件的变形发展。薄板屈曲后中面内力在屈曲后的板中面法线方向的分力由式(1)给出［4］:

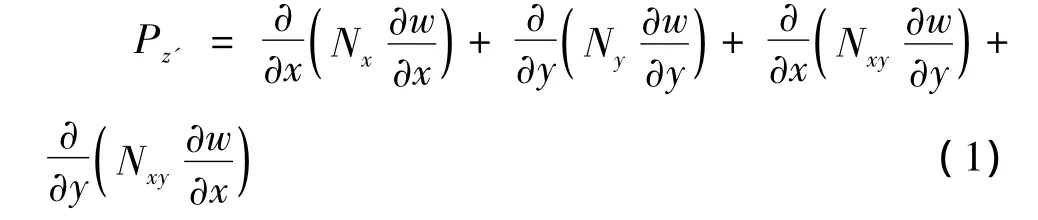
如果将板单元的x，y和z轴与薄壁构件中的n-s-z坐标系的z，s和n轴对应，则板挠度w即为薄壁构件位移 vn，单位宽度膜力 Nx，Ny和 Nxy对应于 σzt，σst和τzst。因此，变位后的中面法线方向上的分量为:

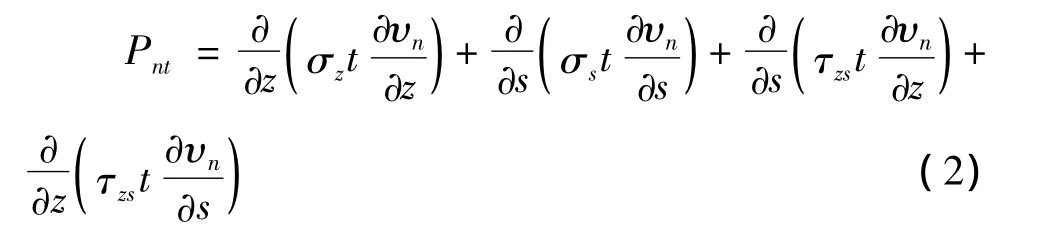
由于应力状态板件发生切线方向位移 υs［5］，因此沿变位后曲线坐标方向的假想面荷载如式(3):

y'方向上的假想的和真正的面荷载之和为:

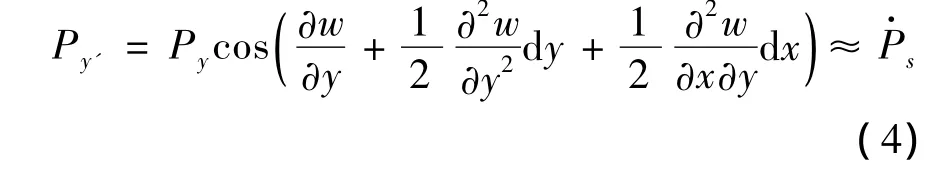
由式(3)和式(4)，得到变位后s方向的总的荷载分量为:

由式(2)和式(5)可以求得薄壁结构中的基本板件在变形后的坐标上的假想荷载。

2.2 假想荷载法的基本方程

假想荷载法是在变形后的截面主轴方向上建立平衡微分方程。这里的假想荷载与以往的说法不一样，指的是变形后坐标轴方向上总力的分量，基本方程如下:

式(6a)～(6c)的方程都是建立在结构变位后的坐标系上，假想荷载和外荷载都往变形以后的主坐标轴方向上(如图1的x'，y'方向)分解，扭矩同样是对截面剪切中心S1取矩得到。

图1中，截面上任意点P在变形前的位置为P0，变形后的位置为P1点。P0点的坐标与变形前的主轴坐标系x轴间夹角为α，荷载qs作用在P0点的切线方向上。截面发生转动，P从P0点移动到了P1点，与此同时，P1点与x轴间的夹角变为α+θ，形心主轴的方向变到图中的x'和y'的方向，S0到S1的位置变化是指截面的剪心位置变化情况。

图1 坐标系随变形的变化Fig.1 Coordinate system changes with deformation

由图1可得，变形后x'和y'方向的荷载分量qxt和qyt以及对剪切中心s1的分布扭矩mzt为:

以x方向的假想分布荷载qxt为例，将薄壁构件变形后坐标方向上的假想面荷载式(2)和式(5)代入(7)式，得:

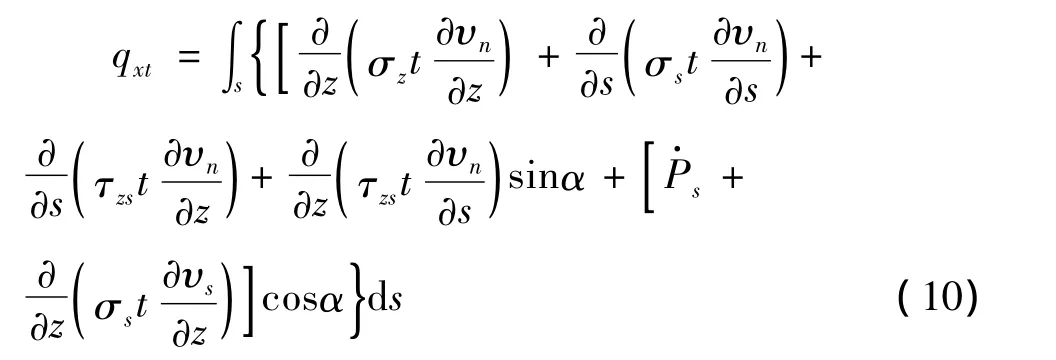
对式(10)的各个部分进行分步积分得:

同理，对变形后y'方向的荷载分量qyt以及对剪切中心s1的分布扭矩mzt做同样的变换得到:

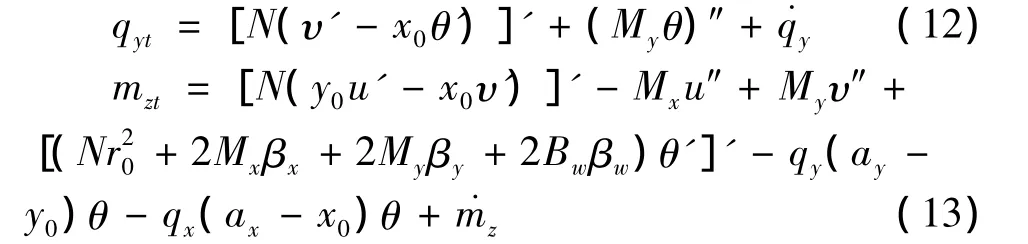
将式(11)～式(13)中变形后x'和y'方向的荷载分量qxt和qyt以及对剪切中心s1的分布扭矩mzt代入到式(6a)～(6c)，就可得到薄壁构件弯扭平衡微分方程:

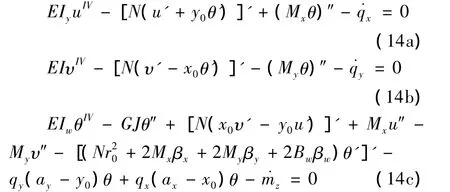
在以上假设下，利用假想荷载法得到的弯扭平衡微分方程组(14a)～(14c)与利用虚功原理［6］得到的结果是完全一致的。通过引入假想荷载法的推导，直观的解释了薄壁构件弯扭屈曲问题用能量法［7-8］进行分析推导时为什么不能引入外荷载的非线性功，也对薄壁构件弯扭屈曲过程中到底发生了什么，产生了什么有了更清楚深刻的理解。

3 数值模拟研究

3.1 研究背景

近几年国内一些桥梁专家在钢-混凝土组合桥梁的研究过程中，开发了竖转钢-混凝土组合拱桥，并成功应用在重庆藻渡大桥等4座桥梁当中。在此基础上，又提出了钢箱-混凝土组合连续刚构桥，其截面主要是U型钢箱和预制混凝土桥道板组成，在桥梁施工过程中，首先吊装好U型钢箱，然后在安装预制混凝土桥道板，截面如图2。笔者以此为背景，以变截面长悬臂开口钢箱为研究对象，对变截面开口钢箱的稳定问题进行了探讨。

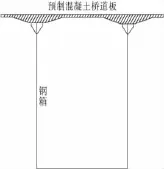
图2 钢-混凝土组合断面示意Fig.2 Steel-concrete composite cross-section

3.2 计算模型

假设以变截面悬臂长度为L，底板跨度W，根部腹板高度H1，自由端腹板高度H2为影响参数，模型中不考虑加劲肋的影响，底板线形采用二次抛物线，将混凝土车道板荷载简化为均布力施加于U型钢箱腹板上，模型分析示意如图3。

图3 模型分析示意Fig.3 Schematic model

有限元分析时选取悬臂长 L分别为50，75，90 m，底板宽度 W 分别为4，6，8 m，H1为4～15 m，H2为2～15 m，钢板厚度均为2 cm。利用ANSYS对不同尺寸结构进行屈曲分析。腹板和底板采用shell63单元模拟，单元厚度为0.02 m。在L=50 m，W=4 m，H1=4 m，H2=2 m时进行了单元网格划分的有限元模型如图4。

图4 单元网格划分后的有限元分析模型Fig.4 Finite element analysis model with the unit meshed

3.3 计算结果

通过计算，变截面开口钢箱在竖向荷载作用下，不同几何尺寸1阶屈曲模态可归纳为4种形态，如图5。

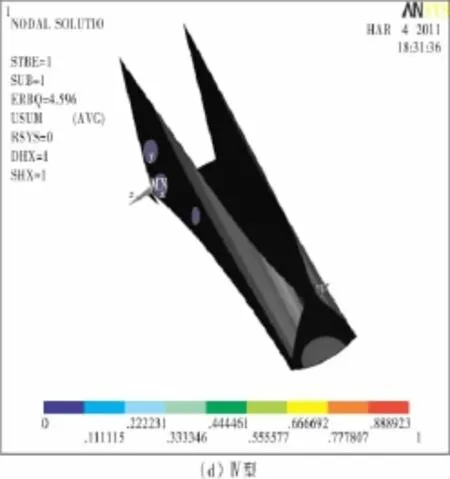
图5 屈曲模态Fig.5 Buckling mode

3.4 结果分析

3.4.1 Ⅰ型屈曲模态

固定端附近底板形成了凸凹不平的波段，屈曲后竖向腹板和底板间的连接线保持原来的直线，竖向腹板截面的轮廓形状保持不变，即:固定端附近底板发生局部屈曲。

3.4.2 Ⅱ型屈曲模态

固定端附近底板和腹板同时形成了凸凹不平的波段，屈曲后竖向腹板和底板之间的连接线由原来的直线发生倾斜，屈曲区域附近底板和腹板差生位移，原来的截面形状和轮廓发生了改变，即:固定端附近底板和腹板发生了畸变屈曲。

3.4.3 Ⅲ型屈曲模态

固定端附近腹板形成了凸凹不平的波段，竖向腹板截面的轮廓形状保持不变，屈曲后竖向腹板和底板之间的连接线没变，即:固定端附近腹板发生了局部屈曲。

3.4.4 Ⅳ型屈曲模态

自由端腹板受到荷载后向内和向下发生位移，但其自身截面形状并未出现凸凹不平的波段，即自由端腹板发生了弯扭屈曲。

分析可知，受竖向均布荷载作用下变截面悬臂开口薄壁构件有3种基本屈曲形态，即板件的局部屈曲、截面的畸变屈曲和构件的整体屈曲。在理想状态，这3种屈曲均属于稳定分岔失稳问题［9］。

悬臂长度依次是50，75，90 m，底板宽度依次是4，6，8 m，在悬臂长度和底板宽度一定的条件下，竖向数值H1变化范围4～15 m，水平数值H2为2～15 m的各种尺寸模型所对应的屈曲模态的计算统计结果如图6。

图6 不同尺寸屈曲模态统计Fig.6 Buckling mode statistics of different sizes

从图6可以得出以下规律:

1)悬臂长度对悬臂开口钢箱屈曲影响较大，当悬臂长度L从50 m增大到90 m时，发生Ⅰ型屈曲的概率显著增多，发生Ⅳ型屈曲的概率显著减少。Ⅱ型屈曲和Ⅲ型屈曲变化不显著，尤其是Ⅱ型屈曲只有在某几中尺寸下才发生。

2)悬臂长度L＜75 m时，底板宽度变化对屈曲影响较小，当跨径增大到90 m时，底板宽度变化对屈曲影响较大，不能忽略。具体来说，发生Ⅰ型屈曲的概率增多，发生Ⅳ型屈曲的概率减少。

3)从 L=50 m，W=4 m，H1=4 m，H2=2 m 最小模型开始，首先发生Ⅰ型屈曲;Ⅱ型和Ⅲ型作为Ⅰ型与Ⅳ型的过渡型态，出现频率很小。H2/L＞0.12左右时屈曲型态均为Ⅳ型。

4 结语

1)目前的假想荷载法由于没有在板件理论的范畴内确定假想荷载，不能得到正确的平衡微分方程。笔者在板件理论的范畴内确定假想荷载，将基本方程建立在变形后的结构上，利用假想荷载法得到的弯扭平衡微分方程，直观地解释了薄壁构件弯扭屈曲问题用能量法进行分析推导时，不能引入外荷载的非线性功的原因，对薄壁构件弯扭屈曲的过程作了更清楚地解释。

2)大量数值模拟分析发现，受竖向均布荷载作用的变截面悬臂开口薄壁构件有3种基本屈曲形态，即板件的局部屈曲、截面的畸变屈曲和构件的整体屈曲，这3种屈曲均属于稳定分岔失稳问题。

3)悬臂长度对悬臂开口钢箱一阶屈曲影响较大，而且当悬臂曾长时，固定端底板屈曲增多，自由端腹板屈曲减少。固定端底板和腹板同时发生屈曲以及固定端腹板发生屈曲为过渡型态，出现较少。当悬臂端高度与悬臂长度H2/L＞0.12左右时均为自由端腹板屈曲。

［1］ Vlasov V Z.Thin-Walled Elastic Beam［R］.Washington，D.C.:National Science Foundation，1961.

［2］ 吕烈武，沈世钊，沈祖炎，等.钢结构构件稳定理论［M］.北京:中国建筑工业出版社，1983.

［3］ 郭耀杰.悬臂构件稳定性理论及其应用［M］.武汉:华中理工大学出版社，1997.

［4］ 童根树.钢结构的平面外稳定［M］.北京:中国建筑工业出版社，2007.

［5］ 徐芝纶.弹性力学［M］.北京:高等教育出版社，2008.

［6］ Trahair N S，Papangelis J P.Flexural-torsional buckling of monosymmetric arches［J］.Structural Engineering，ASCE 1987，113(10):2271-2288.

［7］ Papangelis T P，Trahair N S.Flexural-torsional buckling test on arche［J］.Structural Engineering，ASCE，1987，113(7):1433-1443.

［8］ Papangelis T P，Trahair N S.Flexural-torsional stability of arch［J］.Structural Engineering，ASCE，1987，113(4):889-906.

［9］ 陈骥.钢结构稳定理论与设计［M］.北京:科学出版社，2006.