基于MATLAB的公路桥梁车桥耦合数值计算方法

易晋生，顾安邦，王小松

(重庆交通大学土木建筑学院，重庆400074)

车桥耦合振动的研究最早可追溯到19世纪初期。1847年当列车通过英国Chester铁路桥时由于振动产生挠度过大而导致桥垮塌，此后100多年来，车桥动力相互作用问题一直是各国桥梁设计工作者研究的重点课题［1］。当车辆通过桥梁时，在桥梁自身惯性力和车辆自振惯性力等动载作用下，桥梁变形和受力会大于相同荷载静力作用。尤其当车辆的激振频率和桥梁自振频率相接近时，会发生共振现象，使得桥梁产生过大挠度甚至破坏。

近年来，随着桥梁计算理论和施工技术的不断完善，以及高强轻质材料在桥梁工程中的应用，促使桥梁结构向着跨度越来越大、质量越来越轻、刚度越来越小的体系发展。随着人们对交通运输的需要日益增长，不仅车辆的数量迅速的增长，而且车辆的行驶速汽车与众多的服役期满或损伤的桥梁承载能力不足之间的矛盾也日益突出［2］。此外，振动过大将严重影响到行车的舒适性，更为严重的还将影响到行车安全。有关研究表明，现行规范关于桥梁结构冲击系数的取值是偏不安全的［3］。这两方面因素使得桥梁承受的汽车活载以恒载的比例越来越大，车桥耦合振动效应越趋突出，已成桥梁设计计算重要因素之一。

笔者根据所推导出的车桥动力方程组，利用数学分析软件MATLAB，结合两种计算精度较高而实用的数值计算方法编制了车桥耦合振动计算程序。针对用NEWMARK法求解分离的车辆和桥梁运动方程组时，在每个时间步长内迭代计算直至桥梁响应平稳以提高计算精度。为求解复杂的车桥耦合振动问题提供了简便、实用而且计算精度较高的数值计算方法。

1 车桥模型及振动方程的推导

1.1 车辆模型及车辆运动平衡方程

人们在对车桥相互作用问题的研究过程中建立了各种车桥分析模型，其中，梁的模型都是弹性连续体，而对简化车辆荷载就具有从简单到复杂的各种形式，从最早的不变的移动荷载、考虑惯性力的移动质量，到后面的由弹簧和阻尼器所连接的簧上质量模型以及竖向密贴和竖向非密贴现代车辆模型［4－5］。笔者采用两自由度汽车模型(图 1)，将车辆视为多刚体组成的动力系统，质量集中在车体上，车轮和车体之间的支撑由弹簧和阻尼器来模拟。此车辆共两个自由度，它们分别是车体的沉浮、点头。

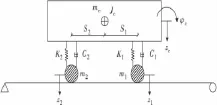
图1 两自由度车辆模型Fig.1 Vehicle model with 2-DOF

假设车辆坐标系以图1中所示为正方向，车体、车架和轮对均视为刚体，不考虑各部件的变形;弹簧和阻尼均为线性;车辆各部件在各自平衡位置附近做小位移的振动。利用达朗贝尔原理对图1所示的两自由度车辆的振动方程进行推导如下。

车体竖向运动平衡方程为:

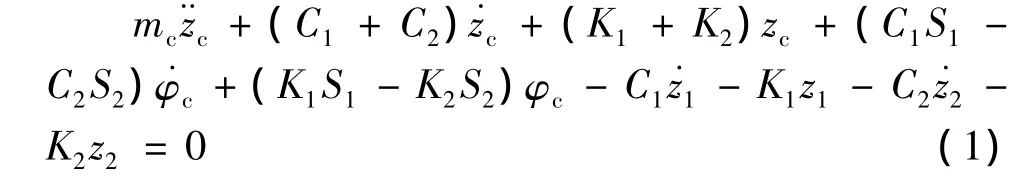
车体点头运动平衡方程为:

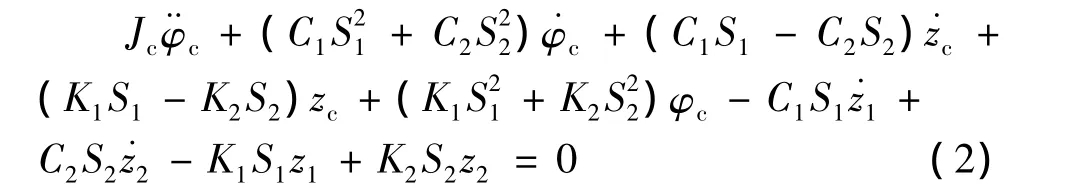
对式(1)、式(2)进行整理并写成如下矩阵方程的形式:

式中:Mc为车辆的质量矩阵;Cc为车辆的阻尼矩阵;Kc为车辆的刚度矩阵;Fc为车辆运动方程的荷载项。具体如下:

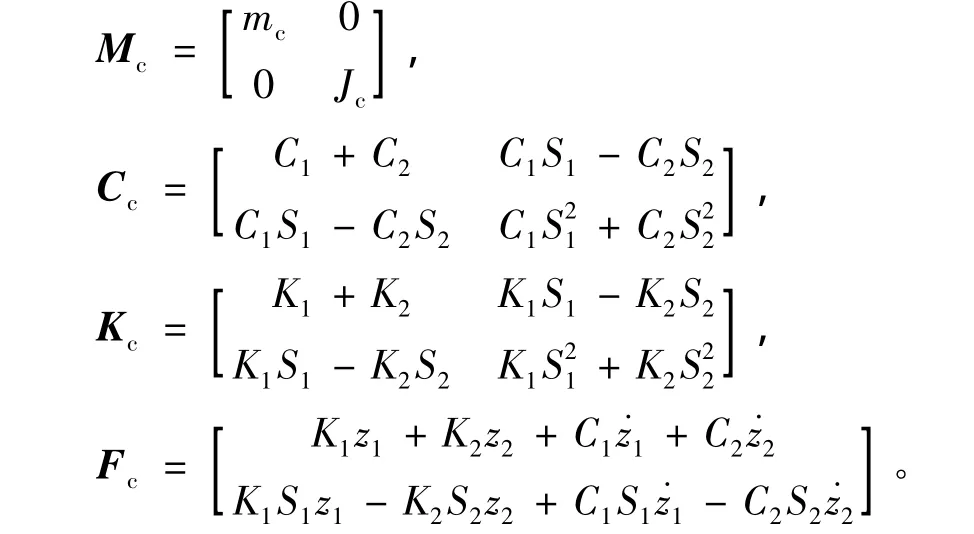
1.2 桥梁运动平衡方程

桥梁是多自由度体系，其运动平衡方程为:

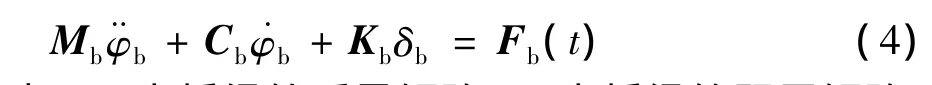
式中:Mb为桥梁的质量矩阵;Cb为桥梁的阻尼矩阵;Kb为桥梁的刚度矩阵;Fb为桥梁运动方程的荷载项。

分别取前、后轮对作为研究对象，可以得到Fb的表达形式，限于篇幅就不一一展开，这里直接给出车辆对桥梁作用的荷载Fb:

2 车桥耦合数值方法及计算原理

车桥耦合振动的分析方法可以分为时域法和频域法，时域法又分为以下两种方法［6-7］:

1)将车辆模型与桥梁模型的所有自由度通过轮轨关系耦合在一起，消除不独立自由度，建立统一的系统运动方程组，进行同步求解。

2)将车桥系统以轮轨接触为界，分为车桥两个子系统，分别建立车桥的运动方程，两者之间通过轮轨接触处的位移协调条件与轮轨相互作用力的平衡关系，采用迭代法求解系统响应。

从计算车桥耦合振动的数值分析方法中作者选用了常用的精度较高而且计算速度较快的龙格-库塔法和NEWMARK法［8］，并结合它们各自的计算特点编制了MATLAB计算程序，并在后面通过算例进行结果比较。

2.1 龙格-库塔法

龙格-库塔法［9］是单步法中的一种，它精确度较高，无需计算高阶导数，就可以达到与泰勒级数方法同样的精度。其基本思路是构造在某些点处的值的线性组合公式，使其按泰勒展开后与初值问题的解的泰勒展开式比较，以相同项系数相等以确定其中的参数。

笔者主要对4阶龙格-库塔法的求解思路进行说明。并选用4阶龙格-库塔法进行计算，采用MATLAB编制了相应的计算程序，对4自由度桥梁与桥梁耦合进行了计算分析。4阶龙格-库塔法的计算公式如下:

2.2 NEWMARK 法

2.2.1 NEWMARK 法计算原理

NEWMARK法［10-11］是结构动力分析中最常用的计算方法之一，1959年N.M.Newmark基于公式(11)、公式(12)发展了一类时间步进法:

参数β和γ定义了时间步内加速度的变化，并决定方法的稳定性与精度特征。对于γ=1/2和1/6≤β≤1/4的典型选择，从包括精度的所有观点来看都是令人满意的。式(1)、式(2)与时间步结束时的平衡方程结合，提供了从i时刻已知的ui，˙ui，¨ui计算i+1时刻的ui+1，˙ui+1，¨ui+1的基础。执行这些计算需要迭代，因为未知的¨ui+1出现在式子的右侧。然而，对于线性体系，修正NEWMARK法的原始公式可以允许使用式(11)、式(12)求解时不迭代。单自由度问题采用NEWMARK法求解的具体步骤如下:

1)初始计算

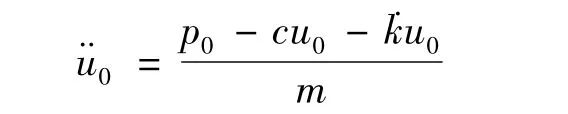
选择Δt

2)对每个时间步i进行计算

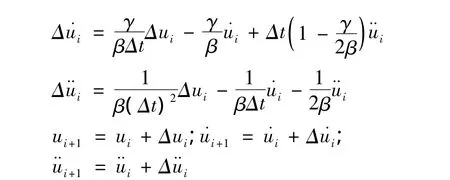
3)对下一个时间步进行循环。而i由i+1取代，对下一个时间步重复2)。

2.2.2 采用NEWMARK法计算车桥分离系统策略

将车桥系统以轮轨接触为界分为车桥两个子系统，分别建立车桥的运动方程，采用迭代法求解系统响应，同时两个系统之间在轮轨接触处满足位移协调条件与轮轨相互作用力的平衡关系。基于MATLAB平台，采用NEWMARK法进行车桥耦合数值计算分析的具体求解思路与过程如下:

1)在t时刻，提取当前桥梁的动力响应作为初始迭代值，并以此为基础通过插值计算车辆轮对处响应的位移、速度和加速度;

2)根据前面求得的车辆轮对处响应的位移、速度求车辆受到的力的作用，并利用NEWMARK法计算t+dt时刻车辆的动力响应;

3)根据前面利用耦合条件计算的轮对响应的位移、速度和加速度和t+dt时刻车辆的动力响应，计算得到车辆对桥梁的作用力;

4)利用t时刻的桥梁响应采用NEWMARK法计算t+dt时刻的桥梁动力响应;

5)重复步骤1)～步骤4)，直至两次相邻计算的桥梁响应收敛，再进行下一个时间步计算。

步骤5)中先根据前后相邻两次计算得到的同一时刻的桥梁响应的差值向量，然后计算其向量的范数作为收敛性的判断的依据。步骤5)的收敛性判断是必要而且关键的，这将在后面的计算中得到证明。

3 算例分析

桥梁参数为:跨径L=30 m，抗弯惯性矩 I=8.65 m4，弹性模量 E=2.943 ×1010N/m，线质量m=3.64 ×104kg/m，泊松比 ν=0.2。

车辆参数为:Mc=5.4 ×105kg，Jc=1.38 ×107N·m2，K1=4.135 ×107kg/m，C1=0 N·s/m，K2=4.135 ×107N/m，C2=0 N·s/m，S1=8.75 m，S2=8.75 m。

计算参数为:桥梁运行速度v=100 km/h，模态阻尼比ζ=0，时间积分步长为0.01 s。

分别采用基于统一方程求解的龙格-库塔法和分离迭代法求解的NEWMARK法对上述算例求解。图2～图4分别为两种方法下简支梁跨中位置的位移响应、速度响应、加速度响应比较。为便于对比，同时给出了采用NEWMARK法而未迭代计算至桥梁振动平衡状态下的结果。

图2 桥梁跨中的位移响应比较Fig.2 Comparison of response of vertical displacement at Mid-span

图3 桥梁跨中的速度响应比较Fig.3 Comparison of response of vertical velocity at Mid-span

图4 桥梁跨中的加速度响应比较Fig.4 Comparison of response of vertical acceleration at Mid-span

由图2～图4可知:

1)由龙格-库塔法和采NEWMARK法迭代计算车桥分离系统都得到了较精确的结果，两者之间的符合度较高。

2)采用NEWMARK法迭代计算车桥分离系统时，在每个时间步内迭代收敛速度较快，并没有因为平衡迭代损失太多时间，并且结果精度较高。

3)采用NEWMARK法计算车桥分离系统时，所得到的跨中挠度位移值与龙格-库塔法的结果最大偏离仅为0.6%;而未进行迭代计算至桥梁振动平衡状态时，其与龙格-库塔法的最大偏离为5.1%。可见，采用NEWMARK法进行迭代计算的计算精度比未进行迭代计算至桥梁振动平衡状态的算法要高。因此，在每个时间步内，迭代计算求解分离的车辆和桥梁运动方程组直至桥梁振动平衡状态是必要且有意义的。

4 结语

应用达朗贝尔原理推导了两自由度车辆模型和桥梁的运动平衡方程，选用了龙格-库塔法和NEWMARK法两种常用的、精确度较高的数值计算方法求解车桥耦合振动。在采用NEWMARK法迭代求解车桥分离双系统方程组时，选择合理的收敛条件作为迭代计算是否终止的依据。通过对比可知，两种数值计算方法都能获得较高的精度。

同时，比较了采用NEWMARK法分析车桥分离系统时，在每个时间步内，迭代计算车辆-桥梁运动方程组直至桥梁振动平衡状态，和未迭代计算车辆-桥梁运动方程组至桥梁振动平衡状态两者的计算结果。研究表明，在每个时间步内迭代计算车辆和桥梁运动方程组直至桥梁振动平衡状态是有必要，其计算精度比未进行迭代计算至桥梁振动平衡状态的算法要高。

［1］ 夏禾.车辆与结构动力相互作用［M］.北京:科学出版社，2002:1-5.

［2］ 卜建清，娄国充，罗韶湘.汽车对桥梁冲击作用分析［J］.振动与冲击，2007，26(1):52-55.

Bu Jianqing，Lou Guochong，Luo Shaoxiang.Analysis on impact effects of bridge due to moving vehicle ［J］.Journal of Vibration and Shock，2007，26(1):52-55.

［3］ 丁南宏，林丽霞，孙迎秋.公路连拱桥在单车荷载下振动的理论和实验研究［J］.兰州交通大学学报，2005，24(3):28-32.

Ding Nanhong，Lin Lixia，Sun Yingqiu.Theoretical and experimental study of highway arcade bridge’s vibration under single vehicle load［J］.Journal of Lanzhou Jiaotong University:Natural Science，2005，24(3):28-32.

［4］ Green M F，Cebon D.Dynamic response of highway bridges to heavy vehicles loads:theory and experimental vibration［J］.Journal of Sound and Vibration，1994，170(1):51-78.

［5］ 曹雪琴，刘必胜，吴鹏贤.桥梁结构动力分析［M］.北京:中国铁道出版社，1987:60-90.

［6］ 韩万水.风-汽车-桥梁系统空间耦合振动研究［D］.上海:同济大学，2006.

［7］ 李小珍，强士中.列车-桥梁耦合振动研究的现状与发展趋势［J］.铁道学报，2002，24(5):113-120.Li Xiaozhen，Qiang Shizhong.State of the art review and trend of studies on vehicle-bridge interaction［J］.Journal of the China Railway Society，2002，24(5):113-120.

［8］ 沈火明，肖新标.求解车桥耦合振动问题的一种数值方法［J］.西南交通大学学报，2003，38(6):658-662.Shen Huoming，Xiao Xinbiao.Numerical method for vehicle-bridge coupling vibrations［J］.Journal of Southwest Jiaotong University，2003，38(6):658-662.

［9］ Steven C C，Raymond P C.工程数值方法［M］.6版.于艳华，傅效群，赵红宇，等，译.北京:清华大学出版社，2010:728-737.

［10］Anil K C.结构动力学理论及其在地震工程中的应用［M］.2版.谢礼立，吕大刚，译.北京:高等教育出版社，2005:124-127.

［11］徐荣桥.结构分析的有限元法与MATLAB程序设计［M］.北京:人民交通出版社，2006:238-246.