量子测距辅助GPS整周模糊度算法

张 豪， 杨春燕， 张 磊， 王浩程

(空军工程大学信息与导航学院，西安 710077)

0 引言

精密型的GPS信号接收机一般都具有伪距和载波相位两种基本的观测量［1］。相对于伪距观测量而言，GPS的载波相位观测量能提供非常精确的定位精度。GPS载波相位差分定位利用了基准站和移动站(用户)之间观测误差的空间相关性，通过差分的方式除去移动站观测数据中的大部分误差，从而实现高精度定位［2］。利用载波相位定位，关键问题就是整周模糊度的解算。对于GPS载波相位观测信号，在观测历元较少的情况下，位置精度因子变化缓慢，会导致整周模糊度解算较为困难。许多学者提出了一些解决的方法，如快速模糊度确定法、模糊度函数法、最小二乘搜索法、最小二乘模糊度降相关平方差法(LAMBDA)等，本文使用LAMBDA算法。

量子定位系统(Quantum Positioning System，QPS)是近几年发展起来的依靠量子频率纠缠和压缩技术的新型定位技术，QPS可以突破无线电导航体制的功率和带宽限制，达到非常高的定位精度，因此受到很多研究机构的重视。本文研究如何在现有的载波相位差分定位中引入QPS技术。用以提高载波相位差分定位在短历元内解算整周模糊度的能力，提高定位精度。

1 载波相位观测方程

考虑载波相位测量误差，则载波相位观测方程为［2］

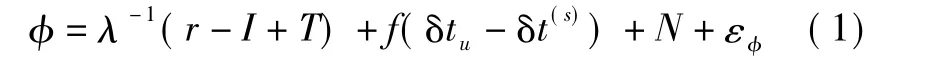
式中:φ为载波相位测量值;λ为卫星发射信号的波长;r为卫星与接收机之间的集合距离;δtu为接收机钟差;δt(s)为卫星钟差;I和T分别为对流层和电离层延时;N为整周模糊度;f为载波频率;εφ为观测噪声。

用两台接收机分别放在基线的两端。其中，一台接收机r作为基准站，其坐标已知，另一台接收机u作为观测站。两台接收机同时同步地观测一颗编号为i的卫星并采集数据。对它们的测量值做差，得单差观测方程为

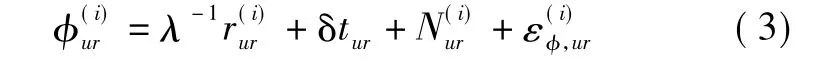
对于卫星j有类似于上式的观测方程。对两颗不同的卫星的单差方程在此做差，即在站间和星间各做一次差分，得双差观测方程为

相对定位的目标是求解出基线向量bur，如图1所示，用户与基准站到卫星i的单差集合距离，等于用户到基准站的基线向量bur在基准站对卫星i观测方向上投影的相反数，即。对于卫星j，类似有。由此可得

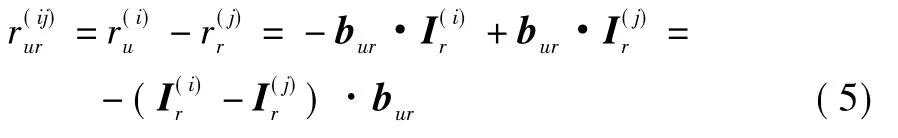
再将式(5)带入式(3)得

图1 单差和双差图Fig.1 Sketch of single difference and double difference

2 整周模糊度解算

式(6)线性化后可概括为［2］

式中:y为接收机给出的双差载波相位测量值向量;Δbur为未知的基线向量;N为需要被求解的双差整周模糊度向量;A和B为常系数矩阵。在这里，未知的测量误差和噪声均被忽略。

利用最小二乘法求解该线性方程，即求满足下式的 Δbur和 N。

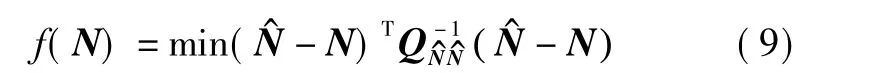
式中，QN^N^为模糊度的协方差矩阵，搜索使目标函数最小的N作为模糊度的最优解即为在少数历元的观测量下进行模糊度搜索时，由于模糊度之间通常具有很大的相关性，整周模糊度的搜索效果并不理想。为了降低模糊度的相关性，提高搜索效率，更准确地确定模糊度，针对以上的问题，LAMBDA算法利用高斯整数转化矩阵Z达到降相关效果［3－5］，设降相关处理后得到的新的模糊度矢量表示为z，相应的协方差阵为有:，使得目标函数转换为

式中:χ2表示搜索范围;为对角矩阵，设上式还可改写为

确定χ2后，根据上式采取条件最小二乘搜索方法即可确定变换后的整周模糊度。将回代

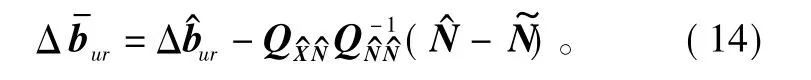
3 量子辅助

量子测距是基于量子力学和量子信息论提出来的一种测距方法，美国麻省理工学院的研究表明，采用具有纠缠压缩特性的量子脉冲代替传统的无线电信号可大幅提升测距系统的精度［6－7］，因为量子脉冲传播时间的测量精度取决于其频谱(脉冲带宽)和功率(单个脉冲所包含的光子数)。当在每个脉冲中大量采用具有量子特性的光子时，脉冲时延的测量精度会大大提高。因为在光子数量密集且频率纠缠的脉冲中，处于纠缠态的光子具有较强相关性，这些脉冲能够以相近的传播速率成束到达，因此增强了信号，提高了检测到达时间的准确程度，进而明显提高了测距的精度［8］。

量子测距辅助GPS定位的示意图如图2所示，在用户的短基线范围内建立发射量子脉冲的信标台，信标台和用户都采用GPS系统时间，信标台发射量子脉冲的时刻与GPS系统时间严格同步，假设所发射量子脉冲的量子压缩数为Cp、纠缠光子数为Et(采用完全纠缠)，量子传输效率为ηen。则发射r个量子脉冲之后所能达到的测距精度为［9－10］

式中:c为光束;δτ为未采用量子压缩和纠缠时单个光子的定时误差。假设量子信标台ECEF坐标为已知，记其到基准站和用户的矢量分别为m和n。则据图2可知

图2 量子测距辅助GPS定位图Fig.2 Sketch of GPS positioning aided by quantum ranging

由于基准站和量子信标台的坐标已知，所以m的确定不依赖用户的观测量，在实际的量子测距中不能直接测出n，而是得到该矢量的长度，即量子信标台到用户的距离。

式中:lK为的真值;δrK为δr在第K个历元的取值。而n与lK的关系为

从上文可知，利用LAMBDA算法求得双差整周模糊度的固定解和求得该条件下基准站到用户的矢量，显然，此时的取值是与的某一个具体取值相对应的，δrK″的大小体现了的误差大小。为此，由式(17)和式(19)可以设定判别

比较 ηK和 3σδr，σδr为 δr的均方值。当 ηK＞3σδr时，认为此时的取值不符合要求;当 ηK≤3σδr时，则认为 N的取值符合要求。

4 仿真分析

根据荷兰Delft大学所发布的载波相位实测数据，在剔除仰角小于10°的GPS卫星数据之后，共得到了6颗卫星的22个历元观测数据。以第1个历元为参考历元，该6颗卫星相对于用户的PDOP变化见图3。

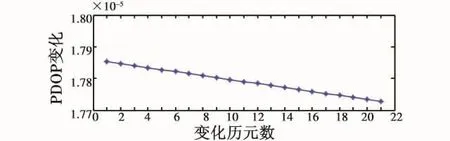
图3 用户的PDOP变化Fig.3 The change of PDOP at different epochs

由此可见，在短观测历元下，定位的PDOP变化是很小的，模糊度的相关性很大，只有采用降相关手段，减小相关性以后才能正确解出整周模糊度。在定位解算过程中，选取仰角最大的卫星为参考卫星，并进行后续的载波相位整周模糊度求解。由于观测的历元数较小，所以参考卫星在整个定位解算过程中并没有发生变化。此外，量子脉冲测距是通过仿真得到的，而并非实际数据。在总的观测历元内，用户与量子信标台的相对距离跟基线距离相比相差不大。

选取如下两种情况进行定位仿真:1)采用LAMBDA算法;2)采用高精度量子脉冲辅助(量子压缩光子个数为2;最大纠缠光子个数为5;传输效率为98.5%)。两种情况得到的基准站到用户的基线矢量求解结果误差分别如图4、图5所示。

图4 基线误差(采用LAMBDA算法)Fig.4 Baseline error of LAMBDE method

由此可见，在高精度量子脉冲测距的辅助下，可以有效提高短观测历元内的整周模糊度求解准确性。

图5 基线误差(采用量子测距辅助)Fig.5 Baseline error aided by quantum ranging

5 结论

利用LAMBDA算法进行降相关处理，可以有效地降低模糊度之间的相关性。高精度量子测距可以限制整周模糊度固定解取值范围，可以有效提高固定解的求解准确性，因此可以改善短观测历元内整周模糊度的准确求解问题。

［1］ 刘基余.GPS卫星导航定位原理与方法［M］.北京:科学出版社，2003.

［2］ 谢钢.GPS原理与接收机设计［M］.北京:电子工业出版社，2009.

［3］ 程云鹏，张凯院，徐仲.矩阵论［M］.西安:西北工业大学出版社，2010.

［4］ 王子茹，李凤斌.综述GPS定位中整周期模糊度求解问题［J］.东北测绘，2000(1):14－16.

［5］ 卢献健.GPS整周模糊度求解理论分析与方法研究［D］.桂林:桂林工学院，2008.

［6］ BAHDER T B.Quantum positioning system［C］//The 36th Annual Precise Time and Time Interval(PTTI)Meeting，Naval Observatory Washington D C，Washington，2004:423－427.

［7］ 王兆华.纠缠双光对的量子定位［D］.西安:陕西师范大学，2010.

［8］ 夏岩.纠缠态的制备及其在量子通信中应用的理论研究［D］.大连:大连理工大学，2009.

［9］ 康乐.量子信息传输及纠缠产生［D］.大连:大连理工大学，2010.

［10］ PAN J W，SIMON C，BRUKNER C，et al.Entanglement purification for quantum communication［J］.Nature，2005，410:1067－1070.