函数奇偶性的多角度理解与应用

☉江苏省连云港高级中学 高 原

函数的奇偶性是函数的一个重要性质，对函数变化的规律可以从对称的角度进行描述，从不同的角度对函数奇偶性进行理解，从而能够对函数奇偶性灵活的应用.

一、定义的理解

1.如果对于函数f（x）定义域内任意一个x，都有f（-x）=f（x），那么函数f（x）就叫做偶函数.

2.如果对于函数f（x）定义域内任意一个x，都有f（-x）=-f（x），那么函数f（x）就叫做奇函数.

如果函数f（x）是奇函数或偶函数，那么我们就说函数f（x）具有奇偶性.

对上述定义可从以下三个角度理解：

（1）任意性：要对定义域内任意x都满足条件，所以奇偶性是函数整个定义域上的性质，区别于单调性是某个区间上的性质.

（2）符号f（-x）=f（x）用文字语言描述是当自变量互为相反数时函数值相等；f（-x）=-f（x）用文字描述为当自变量互为相反数时函数值也互为相反数.

（3）一般地，奇函数的图像关于原点对称，反过来，如果一个函数的图像关于原点对称，那么这个函数是奇函数；偶函数的图像关于y轴对称，反过来，如果一个函数的图像关于y轴对称，那么这个函数是偶函数.

二、函数奇偶性的判定方法

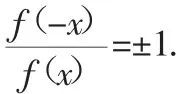
2.借助函数的图像判定函数奇偶性.

3.性质法判定：

（1）在两个函数定义域的公共部分内，两奇函数之积（商）为偶函数；两偶函数之积（商）也为偶函数；一奇一偶函数之积（商）为奇函数（注意取商时分母不为0）；

（2）偶函数在区间（a，b）上递增（减），则在区间（-b，-a） 上递减（增）；奇函数在区间（a，b）与（-b，-a）上的增减性相同.

例1 判断下列函数是否具有奇偶性：

（1）f（x）=x+x3+x5； （2）f（x）=x2+1；

（3）f（x）=x+1； （4）f（x）=x2+1，x∈［-1，3］.

解析：（1）函数f（x）=x+x3+x5定义域为R，

因为f（-x）=-x-x3-x5=-f（x），所以函数f（x）=x+x3+x5为奇函数.

（2）函数f（x）=x2+1定义域为R，f（-x）=x2+1=f（x），所以函数f（x）=x2+1为偶函数.

（3）f（-1）=0，f（1）=2，所以f（x）=x+1不是偶函数；f（-2）=-1，-f（2）=-3，所以f（x）=x+1不是奇函数.

（4）因为定义域不关于原点以称，所以f（x）=x2+1，x∈［-1，3］既不是奇函数，也不是偶函数.

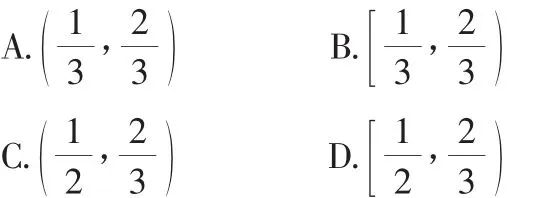
答案：

解析：由于f（x）是偶函数，故f（x）=

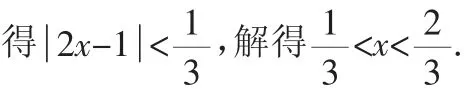
（1）求a、b、c的值；

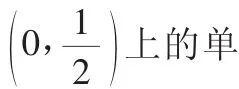
解析：（1）因为f（-x）=-f（x），所以c=0.

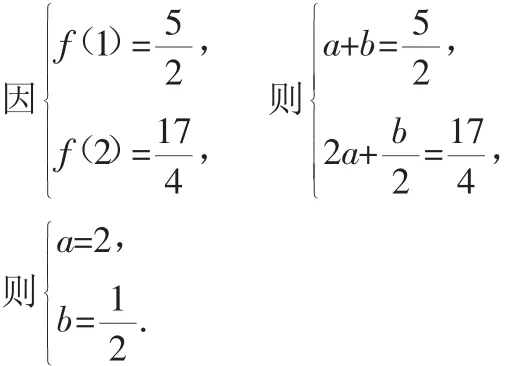
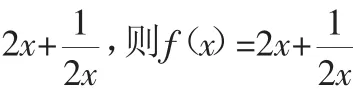
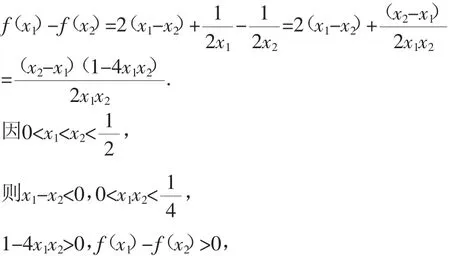
例4 已知函数f（x）=

（1）判断并证明函数的奇偶性；

（2）函数g（x）=f（4-x），比较g（-1）与g（6）的大小.解析：（1）是偶函数.定义域是R.

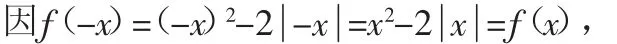
则函数f（x）是偶函数.

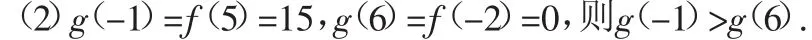
三、误解分析

1.判断函数是否具有奇偶性，首先要看函数的定义域是否关于原点对称.即函数定义域关于原点对称是函数具有奇偶性的必要条件.

例5 判断函数y=x2，x∈［-1，1）的奇偶性.

解析：由于定义域不关于原点对称，所以是非奇非偶函数.

2.判断函数是否具有奇偶性，一般要对解析式进行化简，这样才能得出正确结论.

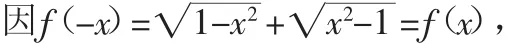
则f（x）是偶函数.