不等式问题中数形结合思想的妙用

☉江苏省丹阳高级中学 盛文萍

数形结合是高中数学中重要的思想方法之一，利用数形结合的方法有时可以快速寻找到解题思路，本文就数形结合的方法求解与不等式相关的问题，举例分析.

一、解一元二次不等式

例1 设a∈R，若x＞0时均有［（a-1）x-1］（x2-ax-1）≥0，则a=______________.

解析：本题按照一般思路，则可分为以下两种情况：

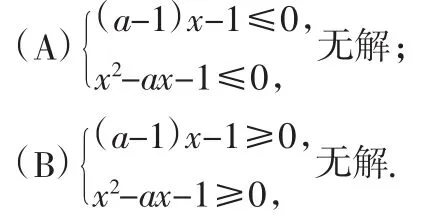
因为受到经验的影响，会认为本题可能是错题或者解不出答案.其实在x＞0的整个区间上，我们可以将其分成两个区间（为什么是两个？），在各自的区间内恒正或恒负.

我们知道：函数y1=（a-1）x-1，y2=x2-ax-1都过定点P（0，-1）.

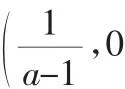
二、解含参不等式

例2已知f（x）=m（x-2m）（x+m+3），g（x）=2x-2.若同时满足条件：

①∀x∈R，f（x）＜0或g（x）＜0；

②∃x∈（-∞，-4），f（x）g（x）＜0.则m的取值范围是______.

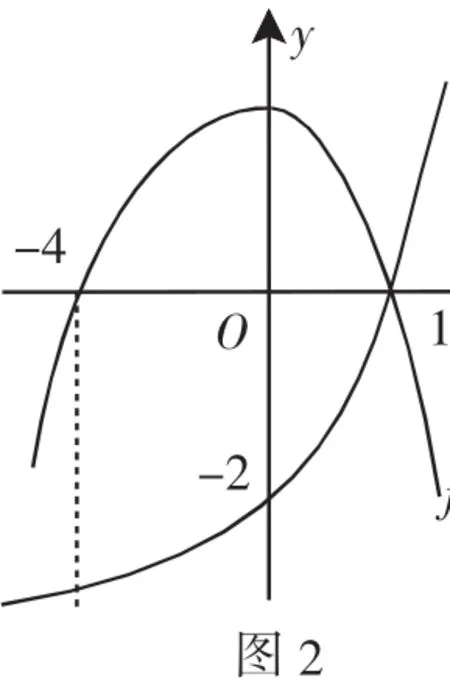
解析：画出函数g（x）的图像，如图2.

如满足条件②，则2m＜-4，解得m＜-2.

综上，-4＜m＜-2

点评：利用数形结合处理不等式问题，常根据不等式的两端构造两个函数，作出这两个函数的图像，根据两个图像的交点和位置关系，即可获解.

三、解绝对不等式

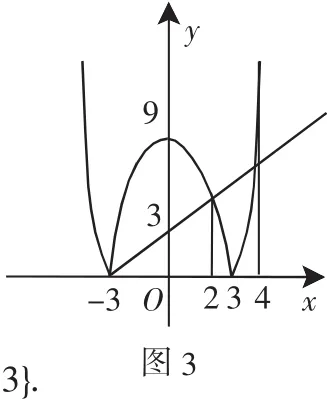
点评：在作图像的时候，要注意图像的准确性及完备性.

四、解高次不等式

对于一元高次不等式，通常是利用数轴标根法来解决.

例4 解不等式（x2+5x+6）（2x2-x-1）＞0.

解析：原不等式可化为（x+3）（x+2）（2x+1）（x-1）＞0.

五、解抽象不等式

例5若f（x）为奇函数，且在（-∞，0）内是增函数，又f（-2）=0，则xf（x）＜0的解集为（）.

A.（-2，0）∪（0，2）B.（-∞，-2）∪（0，2）

C.（-∞，-2）∪（2，+∞）D.（-2，0）∪（2，+∞）

解析：本题可根据题设条件先作出函数f（x）在（-∞，0）内的大致图像，由对称性（奇函数的图像关于原点对称）得出f（x）在（0，+∞）上的图像，从而数形结合、直观求解.

因f（x）为奇函数，且在（-∞，0）内是增函数，f（-2）=0，

则作出函数f（x）在（-∞，0）及（0，+∞）内的大致图像如图5.当-2＜x＜0时，f（x）＞0，xf（x）＜0；当0＜x＜2时，f（x）＜0，xf（x）＜0.

故不等式xf（x）＜0的解集为（-2，0）∪（0，2）.故选A.

点评：若函数f（x）是奇函数，则其图像关于原点对称.此类抽象函数问题利用对称性和数形结合，常可迎刃而解.