整体思想在解题中的应用

☉江苏苏州市南环中学校 杨 兵

数学中的“整体思想”是学生必须掌握的数学思想方法之一.整体思想方法就是指在研究问题时从整体出发，对问题的整体形式、结构、特征进行综合分析、整体处理的思想方法.利用整体思想分析问题，往往可以找到最合理、最简捷、最实用的解题方法，起到化难为易、化繁为简的作用，提高解题效率.整体思想涉及的形式较多，这里主要对“整体观察”“整体代入”“整体换元”“整体构造”在解题过程中的作用，结合初中毕业专题复习，从下面的例题中让学生进一步掌握整体思想的解题技巧，从而提高学生的解题能力.

一、整体思想在因式分解中的应用

例1 把-7（2x-y）2+4（x+y）2-12（2x2+xy-y2）分解因式.

分析：本题中重点观察后面的2x2+xy-y2，先分解成（2x-y）（x+y），然后把前面的（x+y）和（2x-y）看做两个整体.

例2 把（x2+3x-2）（x2+3x-6）-32分解因式.

分析：先把（x2+3x）看成一个整体，然后展开，再次因式分解.

二、整体思想在解方程（组）中的应用

检验后得x=±1是原方程的根.

三、整体思想在求值中的应用

例5 已知x2-4x+3=0，求（x-1）2-2（1+x）的值.

分析：把x2-4x当做一个整体，把（x-1）2-2（1+x）展开，不需要利用方程求解出x的值，整体代入即可.

解：（x-1）2-2（1+x）

由x2-4x+3=0，得x2-4x=-3.

所以，原式=-3-1=-4.

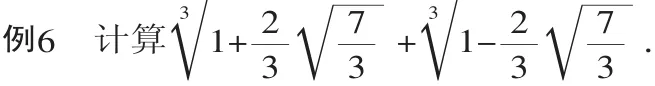
分析：要分别计算出两个三次根式的值比较困难，本题可将计算结果看做一个整体t.

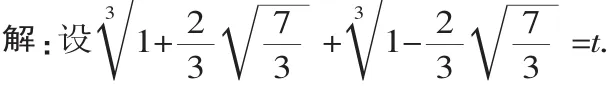
两边三次方后得，t3+t-2=0，（t-1）（t2+t+2）=0.

因为t2+t+2＞0，所以t-1=0，所以t=1.

四、整体思想在求函数解析式时的应用

例7 已知ay+b与cx+d成正比例（a、b、c、d都是常数，且a≠0，c≠0），当x=2时，y=-1；当x=3时，y=1.求y与x之间的函数关系式.

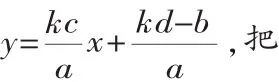
解：设ay+b=k（cx+d）（k≠0），则ay=kcx+kd-b.

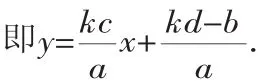
则所求的y与x之间的函数关系式是y=2x-5.

综上所述，整体思想是中学数学的一种非常重要的思想与方法.在数学教学过程中，灵活利用整体思想，可以开拓学生的解题思路，强化化归能力，提高学生的数学综合素质.