浅谈初中数学观点下的“相等”与“不等”关系

2012-08-27福建厦门市杏南中学黄志鲲

中学数学杂志 2012年2期

☉福建厦门市杏南中学黄志鲲

新人教版八年级上《数学》教科书第十二章《轴对称》有一个“实验与探究”材料《三角形中边与角之间的不等关系》，它是在学习了三角形中“等边对等角”和“等角对等边”性质后提出来的反思：如果三角形的边（角）不相等，那么它们所对的角（边）的大小关系怎样？大边所对的角也大吗？

第一个问题很容易回答，我们知道“真命题的逆否命题一定也是真命题”，因此我们可以直接下结论：如果三角形的边不相等，则这些边所对的角也不相等；反之，如果三角形的角不相等，则它们所对的边也不相等.

对于第二个问题，针对学生的认知水平，教材利用轴对称的方法解决问题：已知△ABC中，AB＞AC，将△ABC折叠，使边AC落在边AB上，点C落在边AB的点D处，如图1，根据“三角形外角大于不相邻的内角”可知∠ADE＞∠B，即∠C＞∠B，因此有“三角形中大边对大角”.

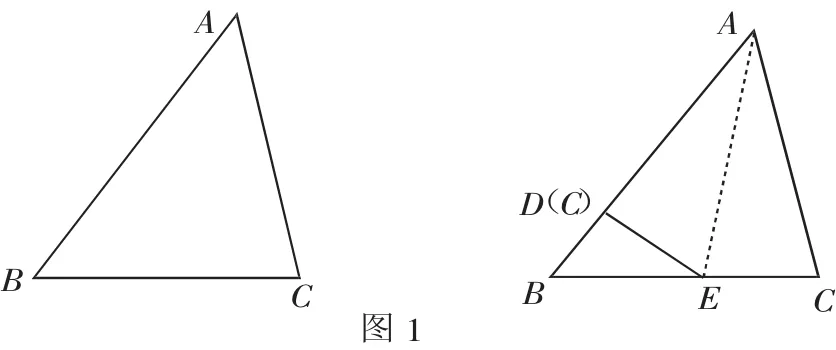
对于“大角对大边”的证明，则可以采用作BC边的垂直平分线的方法解决，如图2.

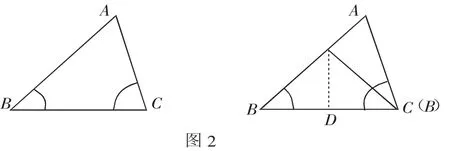
我们再次回顾上面的思维过程：由等腰三角形中很普通的结论“等边对等角”和“等角对等边”，“理所当然”地多想了一步“如果不相等会怎样”——是“大边对大角”还是“大边对小角”？

其实这不是“多此一举”，更不是“哗众取宠”！这个“不等”，不仅将学过的“轴对称”用于比较线段和角的大小，从“动手”到“动脑”，将“轴对称”提升到新的应用层次，而且从思维角度看，这一步“多想”蕴含着数学思维的严密性，对等腰三角形边角关系的学习没有仅仅满足于“相等”，而是继续研究与其密切相关的“不等”，让问题从“面”上彻底解决，而不仅仅解决一个“点”.这就是数学的严谨和求真，这也是教材要传递的一种信息，数学的学习不仅包括数学知识，还包括学习数学知识所需要的态度与素养.

至此，教材将三角形中的“相等”与“不等”关系演绎得淋漓尽致，从“等角对等边”到“大角对大边”，从“等边对等角”到“大边对大角”，犹如化蛹成蝶，实现了美丽的蜕变，不禁让人拍案叫绝！在中学教材中将数学的一种思想方法挖掘到如此深刻，是非常少见的，这不得不让人对这对“不同寻常”的关系刮目相看.“相等”和“不等”是数学中最基本的关系，它们既对立又辩证统一，在一定的条件下，它们又能互相转化，相辅相成，在许多方面都闪耀着智慧的光芒，让人惊叹不已.

这里笔者就初中义务教育阶段的数学谈一些个人的理解.

对于“相等”与“不等”，从狭义上理解，就是两个数或量的大小关系.人类最早接触的数学就是两数的大小，即两数a和b的关系是“a＞b”或“a=b”或“a＜b”三者取其一，进而演变成：对于任意实数 a，必有“a＞0”或“a=0”或“a＜0”，或其他类似的表述，结论存在多种可能就给我们提供了“分类讨论”的基础.

从广义上理解，“相等”与“不等”可以看做是“符合”或“不符合”某种条件，而“相等”是一种“临界状态”，往往是我们考虑的重点，也是解决问题的突破口，但“不等”同样也很重要，因为在茫茫的“数海”中，能够“相等”的毕竟是少数，我们有什么理由不管它们呢？这样，我们的视野一下子就开阔了：“相等”与“不等”是事物的正反两面，它是事物的全面反映！它们之间可能是一种和谐的“量变”，也有可能是一种爆发的“质变”.在“相等”与“不等”的思考和探索中，我们将不断地感受到数学的精辟和奇妙.

笔者以初中数学中几个比较典型的例子进行说明.

1.在探索一元二次方程判别式Δ=b2－4ac与方程的实数根的关系中，考虑到被开方数Δ=b2－4ac≥0，就有了以下的结论：（1）当Δ＞0时，方程有两个不相等的实数根；（2）当Δ=0时，方程有两个相等的实数根；（3）当Δ＜0时，方程无实数根.

例1 关于x的方程x2+ax+1=0，何时有两个相等的实数根？两个不相等的实数根？无实数根？

先解方程 Δ=a2－4=0 得 a=±2，然后在三个区间（－∞，－2），（－2，2），（2，+∞）各取一个数（如：－3，0，3）代入 Δ=a2－4 验证，当a=－3 和 a=3 时 Δ＞0，当 a=0 时 Δ＜0，故可以得出结论：当 a=±2时，方程有两个相等的实数根；当a＜－2或a＞2时，方程有两个不相等的实数根；当－2＜a＜2时，方程无实数根.

注意：初中阶段不要求解一元二次不等式，因此关于含参的二次方程实数根的问题可以通过一元二次方程来解决，其中验证部分涉及二次函数的连续性问题.

在处理不等式或函数的大小比较问题，我们通常借助数形结合，转化为方程来解决.

（2）x取何值时，二次函数y1=x2的值小于一次函数y2=x+2的值？这里也是要解决“不等”问题，同样我们先过渡到“相等”，令y1=y2，即x2=x+2，解得x1=-1，x2=2，利用函数图像我们很快就得到：当-1＜x＜2时x2＜x+2，即y1＜y2.（见图4）

3.勾股定理逆定理：若△ABC三边a，b，c，最长的边c满足c2=a2+b2，则c边所对的角C是直角.在人教版中是用“同一法”证明的：先作一个Rt△A′B′C′，直角边分别是a和b，由勾股定理可知，斜边A′B′2=a2+b2=c2=AB2，两个三角形三边对应相等，故△A′B′C′≌△ABC，因此∠C=∠C′=90°.

这时我们可以进一步问：若c2≠a2+b2，∠C还是直角吗？这个问题马上引发了学生的学习热情，多数学生可以猜想到结果：“若c2＞a2+b2，则c所对的角是钝角；若c2＜a2+b2，则c所对的角是锐角”，但对于结论如何解释却无从下手.这个结论在高中学习了三角函数的余弦定理就可以证明，但在初中阶段我们可以利用《几何画板》进行演示，让学生更加直接地理解和掌握这个知识.

从数学的实质上看，每一次的“相等”都必然伴随着“不等”，例如“角平分线的性质”、“线段垂直平分线的性质”、“圆上的点到圆心的距离相等”、“直线与圆的位置关系”、“方程与不等式”、“函数或代数式最值问题”等等，这里就不再一一赘述.随着我们对“相等”与“不等”的进一步探究，使我们对问题的认识更加全面，对问题的分析更加透彻，对数学的理解更加深刻.