探索有意义学习的数学课堂教学模式

☉广东省广州市赤岗中学 牛应林

一、有意义学习教学理论国内外研究现状

有意义学习的观点最早由美国著名教育心理学家奥苏泊尔（David.P.Ausubel）提出，他在反思布鲁纳（Jerome Seymour Bruner）提出的认知—发现学习理论的基础上，从20世纪50年代中期开始致力于有意义言语材料的学习与保持的研究，有意义学习理论在60年代提出后，受到中小学教师的欢迎.奥苏泊尔认为，有意义学习的实质是符号所代表的新知识与学习者认知结构中适当的观念建立非人为的和实质性的联系.奥苏泊尔的有意义学习理论告诉我们：学生学习应该是有意义的接受学习和有意义的发现学习，有意义学习的过程即原有观念对新观念加以同化的过程，提出了渐进分化和综合贯通两个教学原则，“先行组织者”的教学策略.

20世纪90年代以来，随着心理学家对人类学习过程认知规律研究的不断深入，认知学习理论的一个重要分支—建构主义学习理论在西方逐渐流行，建构主义学习理论的核心就是“以学生为中心”.建构主义理论告诉我们：学习过程不是学习者被动地接受知识，而是积极地建构知识的过程.根据建构主义的理论，要有效地完成知识的建构过程，学生必须由外部刺激的被动接受者和知识的灌输对象转变为信息加工的主体、知识意义的主动建构者；教师必须由知识的传授者、灌输者转变为学生主动建构意义的帮助者、促进者.

自从20世纪90年代中国推出新课程实验以来，福建师范大学余文森教授，以有意义学习这根主线，在理论上作了很好的科学描述和拓展；浙江师范大学教育评论研究所傅宝英教授，也对有意义学习的内涵，从人本主义出发，提出六个方面的教学策略；《四川师范大学学报（自然科学版）》1992年05期，徐发吉发表的《初中数学概念的有意义学习与教学》；《河西学院学报》2004年03期，谢海燕，傅敏发表的《奥苏泊尔和罗杰斯有意义学习理论的比较与启示》；《数学通报》2004年04期，陈柏良发表的《基于奥苏泊尔有意义学习理论的对数函数概念的引入教学》；《苏州大学》2008年，顾文娟发表的《高中数学有意义学习的教师监控》；《南昌高专学报》2010年03期，杨超发表的《奥苏泊尔的有意义学习理论在数学教学中的应用》；《高中数学教与学》2011年08期，徐光考发表的《基于有意义接受学习的数学课堂教学策略》等等都对有意义学习做了进一步的研究.

二、有意义学习的数学课堂教学

中学数学课堂教学，遵循“以学生为中心”的教学理念，根据教育心理学理论，研究如何让学生主动参与课堂，挖掘学生学习数学的“认知”和“非认知”两方面的因素，以潜能开发观、学生主体观、整体效能观、合作竞争观为指导，引导学生进行有意义学习.利用适当的引导性材料对新内容加以定向引导，建立新旧知识之间的联系，从而对新学习内容起固定、吸收作用.通过让学生独立解决问题和合作交流学习，教会学生如何学习，如何提高课堂教学效率.

数学学习活动过程，就是新的数学学习内容与学生原有数学认知结构中的有关内容相互作用，从而形成新的数学认知结构或扩大原有数学认知结构的过程.从直接参与新的数学学习的活动过程来分析，除原有这些数学认知结构外，还包含学生现有的知识水平和学习能力.无疑，这些对数学学习起着直接的作用，影响着数学知识与技能的掌握.

数学学习受到情感、意志、动机、兴趣、个性品质的影响，它们虽不直接参与数学学习的认知活动，但它是以尊重学生的发展为前提，对数学学习起着推动、增强、坚持、调节控制等作用.

三、有意义学习的数学课堂教学模式

浙江省富阳市教研室数学教研员章敏毅老师主持的“新课堂初中生数学有意义学习培养的研究”成果之一是，新数学课程标准下，构建以学生“自主、合作、探究”为学习方式的全新的课堂教学动态场.在课堂教学中，不能尽以灌输的方法来操作.而是从传统的数学教学思想到现代数学教学理念的转变中，逐步创设以新课程背景下的课堂教学的积极势态，主要体现在以下四个方面活性因素的激活：

1.学生对意义符号的理解，既是学生自身内部个体对课程意义的内化，也是学生个体对课堂运行的心理行为，它是课堂教学的基础；

2.教师的教与学生的学之间的心理沟通，它是主体间的信息和情感交流.这种交流就是课程意义在师生、生生中创造与分享的一个过程；

3.课堂教学应该是一项发展性活动，必须人人参与才能顺利完成.学生个性如果不参与活动，课程的意义就不会对其产生任何影响.课堂教学中个体参与强调学生个体的能动性，凸现学生个体在课堂活动中的地位、作用；

4.课堂教学应该是教师的教与学生的学的统一，这种统一的实质就是师与生、生与生之间的互动，合作学习.

这里主动参与是核心，其它三个因素围绕核心，突出了主体行为的因果性、依存性、共振性和多样性，从而形成一个有利于学生学习的动态场.只有在这样的课堂下，对学生开展有意义学习培养才会有新的突破.

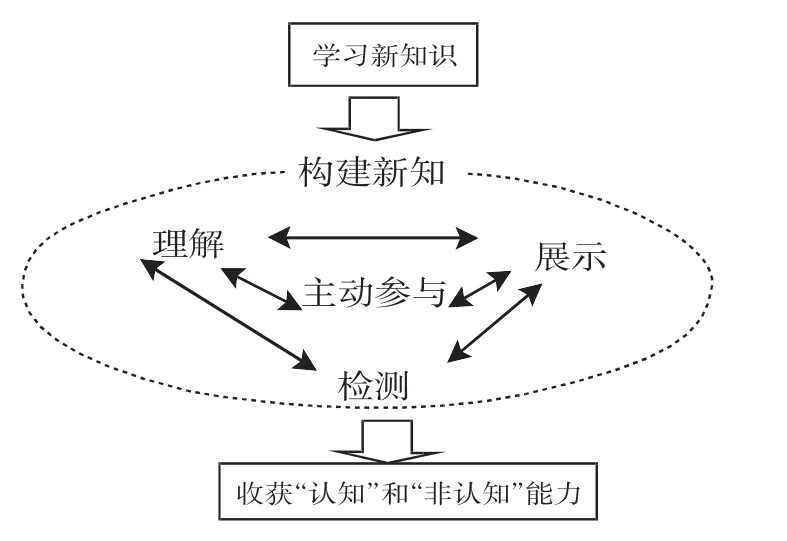
有意义学习的数学课堂教学模式

四、有意义学习的数学课堂教学模式实践

由中华人民共和国教育部主管，中国人民大学主办的期刊《高中数学教与学》（ISSN1674-8794）2011年08期，转载徐光考于2011年发表在《中国数学教育》高中版上的《基于有意义接受学习的数学课堂教学策略》一文.该文比较详细地介绍了奥苏泊尔的有意义接受学习理论，并从先行组织者策略、构建合适的“潜在距离”策略、站在系统的高度传输知识策略等三方面阐述有意义接受学习理论在中学课堂教学中的运用，以数学归纳法和高中数学基本不等式为例详细介绍三种策略的使用，非常精彩.这里仅仅介绍在有意义学习教学理论指导下，把中学数学课堂教学看成一个动态场，举出一个例，说明有意义学习的数学课堂教学模式的实际操作程序.

1.学习新知.采用有意义学习理论的先行组织者策略，发挥旧知识的迁移作用，以旧引新，为学生解决尝试问题铺路架桥.例如在讲解三角形全等概念时先让学生做个小实验，通过作数学实验的亲身体验，让学生互动，总结出三角形全等概念.

在硬纸板上挖一个三角形的洞，再挖一个点O作为旋转中心，把挖好的硬纸板放在黑板上，先在黑板上描出这个挖掉的三角形图案（△ABC），然后围绕旋转中心O转动硬纸板，在黑板上再描出这个挖掉的三角形（△A′B′C′），移去硬纸板.

（1）观察线段OA与OA′，OB与OB′，OC与OC′有什么关系？

（2）观察∠AOA′，∠BOB′，∠COC′有什么关系？

（3）观察△ABC与△A′B′C′形状和大小有什么关系？

2.构建新知.采用有意义学习理论的构建合适的“潜在距离”策略，根据教学目标，设置探究问题，以问题引路，大胆放手让学生自己尝试去解决问题，展示学生个人成果，享受知识同化的过程.例如在讲如何解一元一次不等式组时，从解一元一次不等式讲起，逐步推进，最终让学生知识同化.

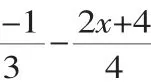
变式1：求例1的非负整数解.

变式2：（假如在例1的基础上再加一个不等式，组成不等式组，如何解？）

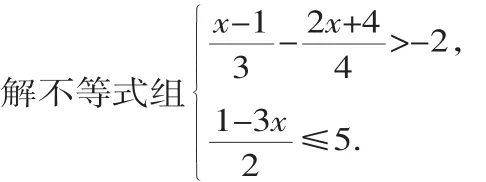
通过这一组例题和变式，让学生复习巩固解一元一次不等式基础上，对一元一次不等式组的解方法有了较深的理解.由于新旧知识之间的“潜在距离”把握适度（在学生的最近发展区内），学生积极思考，乐于交流，从而建立起新旧知识合理和本质的联系，在此基础上进行拓展训练.

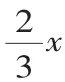
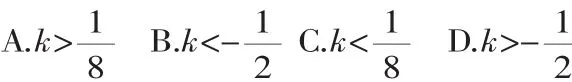
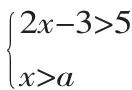
三层练习：3.已知一次函数：y1=3x+5，y2=－2x－1，在同一坐标系中的图像如图所示.

（1） 当x_____时，y1＞y2；（2）当x_____时，y1≤y2+1.

课堂教学的目的是为了学生更有效的学习，紧紧围绕“结论与过程的统一，认知与情意的统一”两个方面来把握，力求探索挖掘学生数学学习的“认知”和“非认知”两个因素间的规律.由于有意义学习的数学课堂教学模式仅仅是探索阶段，让数学课堂成为动态课堂的探索路子还很长，因此还需要倍加呵护，才能迎来生机勃勃的繁荣之日.

1.徐发吉：《初中数学概念的有意义学习与教学》，《四川师范大学学报（自然科学版）》1992年05期.

2.谢海燕，傅敏：《奥苏泊尔和罗杰斯有关意义学习理论的比较与启示》，《河西学院学报》2004年03期.

3.陈柏良：《基于奥苏泊尔有意义学习理论的对数函数概念的引入教学》，《数学通报》2004年04期.

4.顾文娟：《高中数学有意义学习的教师监控》，《苏州大学》2008年.