浅谈反函数的性质及应用
2012-08-27江苏省丹阳市第五中学王金玲
☉江苏省丹阳市第五中学 王金玲

☉江苏省丹阳市第五中学 王金玲
反函数是函数一章的重点,它的性质如定义域、值域、单调性、奇偶性、图像的对称性等常被作为高考考查的重点,本文总结了反函数的几个常用性质,记住它们可以直接解决反函数的一些常见问题,从而避免复杂的运算,达到事半功倍的效果.
若函数y=(fx)(x∈A,y∈C)存在反函数y=f-(1x),则有下列性质:
①y=f-1(x)与y=f(x)的定义域与值域互换;
②y=f(x)⇔x=f-1(y)(x∈A,y∈C);
③y=f-1(x)与y=f(x)的图像关于直线y=x对称(而不是y=f(x)与⇔x=f-1(y)的图像关于直线y=x对称);
④函数y=f(x)(x∈A,y∈C)的图像关于直线y=x对称的充分必要条件是f-1(x)=f(x);
⑤若函数y=f(x)(x∈A)为单调函数,则y=f-1(x)(x∈C)也是单调函数且单调性一致,即原函数与反函数在相应区间上具有相同的单调性;
⑥若函数y=f(x)(x∈A)为奇函数,则y=f-1(x)(x∈C)也是奇函数(注意偶函数是没有反函数的);
⑦f-1[f(x)]=x(x∈A,A为定义域),f[f-1(x)]=x(x∈C,C为值域);
⑧若y=f-1(x)与y=f(x)的图像有交点,则交点必在直线y=x上或交点关于直线y=x对称;
⑨若函数y=f(x)(x∈A)为增函数,则y=f(x)与其反函数的图像的交点必在直线y=x上;
⑩(a,b)在y=f(x)的图像上⇔(b,a)在y=f-1(x)的图像上.
例1(2007年高考天津)函数y=log2(x+4)(x>0)的反函数是_________.
解:先求原函数的值域,它就是反函数的定义域,由x>0得x+4>4.
则y=log2(x+4)>log24=2,原函数的值域是(2,+∞),它就是反函数的定义域,再由原式解出x=2y-4,反函数为f-1(x)=2x-4(x>2).
例2 (2008年高考重庆)设P(3,1)为二次函数f(x)=ax2-2ax+b(x≥1)的图像与其反函数y=f-1(x)的图像的一个交点,则( ).

解:因P(3,1)在反函数图像上,由性质⑩得P′(1,3)在原函数图像上,又已知P(3,1)也在原函数图像上,将P(3,1)和P′(1,3)分别代入f(x)=ax2-2ax+b(x≥1)中,得
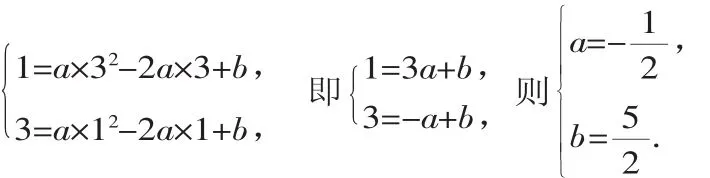
故选C.
此解法避免了求反函数的繁琐过程,既灵活又简练.

解:y=f(x)的图像为双曲线,显然其对称中心为P(-a,1),则其反函数y=f-1(x)的图像的对称中心为P′(1,-a).
又函数y=f(x)的图像关于直线y=x对称,由性质④可知f(x)=f-1(x).
则P与P′也重合,-a=1,即a=-1.

分析:由题意知,只需求出y=f-1(x+1),进而求出y=g(x),可求得g(5)的值.


结论错误,错在哪儿呢? 我们知道y=f(x)与y=f-1(x)互为反函数,但y=f(x+1)与y=f-1(x+1)则不互为反函数,对这点一定要理解.
实际上,可以这样求:由y=f(x+1)两边用f作用得x+1=f-1(y)即x=f-1(y)-1.
故y=f(x+1)的反函数是y=f-1(x)-1.
(2)正是由于(1)的方法,我们可以给出本题的另一个更好的解法.由y=f-1(x+1)两边用f作用得x+1=f(y),则x=f(y)-1,故y=g(x)=f(x)-1.