浅谈新课标下高中数学情景教学策略
2012-08-27浙江省上虞中学金伟祥
☉浙江省上虞中学 金伟祥

高中数学课程标准中提出,数学课程要注重社会、学生发展的需求,教给学生在用数学知识解决生产生活实际问题时应具有的观察视野、思考角度和解决问题的策略,提供开放的和主动思考的空间,让学生发现并提出问题,发表自己的见解,培养学生以辩证的观点认识科学技术与社会的问题.通过实施创设数学课堂教学情境,可以有效的实现新课标的要求,创设教学情境,通过在特定的教学情境中引导学生实施探究活动和合作学习来使学生获取知识,学会方法,培养学生学习数学的兴趣与情感教育,有效的实现三维教学目标的同时,使学生在解答相关数学试题的能力上有所提高,从而提高数学学习成绩.以下笔者结合自身教学实践对高中数学课堂教学情境创设问题进行具体分析.
一、构建“变式”问题情景,培养学生“开放式”数学思维和积极探索能力
(一)通过一般化提高学生化归能力
一般化是由个别到普遍的认识方法,它是从考虑一组对象,进而考虑包含该组对象在内的更大一组对象.把局部、特殊的数学问题上升为整体、普遍的数学问题,再根据问题本身的特性,引出数量关系及位置关系.一般化方法被数学教育家波利亚称为“获得发现的伟大源泉”.对数学问题一般化,就是将数学问题引申,往往能达到“做一题,解一类”的目的.
(二)通过类比达到知识迁移
类比方法是寻找和发现解题途径的常用方法.
案例1.对初学者来说,要解决问题“a为何值时,方程cos2x+cosx=a,对a∈R有解?”有一定的困难,可将这个问题分解为以下几个小问题:
①方程cosx=1,cosx=2,cosx=-0.6有解吗?
②若cosx=a有解,a的范围是什么?
③a为何值时,方程cos2x+cosx=a有解?
通过巧妙设置带有梯度的一系列问题,引导学生由浅入深,自主探索结论,在问题的解决过程中,体验方法:要求a的范围,只需求cos2x+cosx的范围即可,从而产生对“函数与方程”的感性认识.
(三)通过一题多解培养学生发散思维能力
一题多解可以培养学生的发散思维,它是训练学生拓宽思路的重要手段之一,也是学生开拓自身创造性思维的主要方法.
案例2.求实数a的范围,使当x∈[0,1]时,不等式x2-ax+a+1>0恒成立.
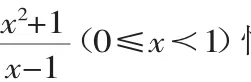
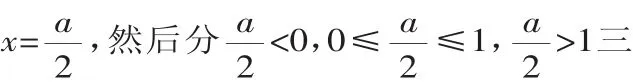
法3(等价转化思想):设原不等式的解集为A,则问题可化为:当a在何范围内取值时,[0,1]⊆A?
法4(数形结合思想):在同一坐标系中,作出函数y1=x2和y2=a(x-1)-1的图像,由图像可知y2=a(x-1)-1恒过定点(1,-1).要使y1>y2在x∈[0,1]时恒成立,直线y2的斜率a应大于-1,所以a∈(-1,+∞).
二、引导归纳、类比猜想情景,促进数学化
在教学中,教师要注意设置合适的情景,让学生在实践中学会用类比法猜想.尤其要注意引导学生进行观察和联想,发现对象之间的相似性.由于相似含义的丰富性,类比的表现形式非常丰富,关系类比,对偶类比,方法类比,模式类比等,都是常见的类比形式.在解题过程中为了寻找问题的解决线索,往往借助于类比方法,以达到启发思路的目的.
案例3.已知P点为棱长是a的正四面体ABCD内一点,求证:点P到正四面体ABCD的四面距离之和为定值.
分析:直接寻求证法比较困难.因为立体几何是平面儿何在空间的推广,所以此处可引导学生利用降维的思路将立体几何问题类比为他们所熟悉的平面几何问题.如下:
已知P点为边长是a的正△ABC内一点,求证:点P到正△ABC的三边距离之和为定值.
易知:只要将点P与点A、B、C分别连接,并利用面积等式S△ABC=S△APB+S△BPC+S△CPA.
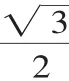
a(其中h1,h2,h3分别为点P到各边的距离,h为正△ABC的边BC上的高).
仿此,对原题,可连接PA,PB,PC,PD.
利用体积等式VA-BCD=VP-ABC+VP-BCD+VP-CDA+VP-DAB,
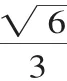
三、创设试题情景,培养学生能力
(一)创设试题情境,考查“双基”
试题的编制应强调基础的掌握和运用,减少单纯的对知识、公式(如三角函数公式)的记忆要求,降低对运算(如指数、对数、幂的计算,复数的概念和计算等)复杂性、技巧性的要求.知识作用的重新定位,就是将评价的内容更多地指向有价值的数学任务和数学活动,将纯粹的数学运算置于问题解决的过程之中.运用情境材料,不但考查学生的数学知识,而且考查学生要能够在几个概念之间比较它们的异同,认识不同概念所对应的不同的解释,能够将概念从文字表述转换成符号的、图形的表述,培养和考查学生的数学交流能力.
(二)创设开放式的试题情景,考查探究能力
“开放式问题”能引导学生深入思考、探究,但它并不一定是难题,这与人们对“开放式问题”的理解是不同的.一般地,人们把“开放式问题”与难题画等号,认为“开放式问题”需要专门的材料.笔者认为这是一个误解.实际上,传统的试题如果借助情景加以改造,只要处理得恰当,就可以转变为一个适合于提高学生思维水平,发展学生数学思维能力的“开放式试题”.如:
案例4. 求证:13+23+33+…+n3=(1+2+3+…+n)2.
这道传统的题目,如果我们仅仅运用数学归纳法予以论证,则许多学生会感到纳闷:结论从哪里来的?如果我们为此问题创设一个归纳、猜想的背景,将其改编为如下题目,则毫无疑问会大大增加学生探讨问题、解决问题的兴趣,同时也比原题降低了难度.
例:仔细观察以下各式,你会得到什么样的结论?能证明你的结论吗?

开放式问题有的涉及的不仅是数学知识,更多地涉及广阔的社会大舞台,需要从多角度、多层面进行探究,做到不同类别知识、众多学科内容、各种技能技巧有机地融合,自觉地打破思维定势,灵活多变地设计多种方案、提出多种猜想、探求多种结果,因此需要灵活、开阔的头脑.
总之,作为从事高中数学教学的一线教师,应该对情景教学进行更多、更深入的研究,并把新课程理念与情景教学结合起来,为学生全面、和谐的发展创造必要的条件,打下良好的基础.
