基于无迹卡尔曼滤波的单站混合定位跟踪算法

刘 翔，宋常建，胡 磊，钟子发

（1.解放军电子工程学院电子制约技术重点实验室，安徽 合肥 230037；2.解放军汽车管理学院，安徽 蚌埠 230011）

0 引言

随着蜂窝网移动通信技术的迅猛发展，移动台无线定位技术已成为研究热点。目前，到达场强（SSOA，Single Strength of Arrival）、到达入射角度（AOA，Angle of Arrival）、到达时间（TOA，Ti me of Arrival）、到达时间差（TDOA，Ti me Difference of Arrival）及其融合而成的混合定位技术，如TDOA／AOA，TOA／AOA等，在商业化应用上已取得成功［1］。但以上定位技术大多要求用于定位的参数由基站或移动台主动支持［2］，且大多为建立静态模型，并在一定的准则（如最小二乘、最大似然等）下求得最优解进而得到估计位置，不能实现实时跟踪的需求。针对移动台的动态跟踪定位问题，提出了一种基于TSOA［3］／TDOA混合被动单站定位模型的无迹卡尔曼滤波跟踪算法。

1 TSOA／TDOA与UKF原理

单站式跟踪通常是一个非线性估计问题，非线性估计中应用最为广泛和成熟的是扩展卡尔曼滤波器（EKF，Extended Kal man Flter）。但是EKF算法存在复杂度高、非线性误差大、应用环境苛刻等问题［4］。为此，Juiler等人提出了 UKF（Unscented Kal man Filter）算法［5］，其各方面性能明显优于EKF算法［6－9］，广泛应用于诸多领域。

1.1 TSOA／TDOA定位实现原理

TSOA／TDOA定位技术是一种基于到达时间和（TSOA）与到达时间差（TDOA）的新型混合定位技术，其定位实现原理图如图1所示。定位系统由定位设备、基站、目标用户三者构成，定位设备发起和实现定位过程，基站和目标用户都是被动参与者。

图1为TSOA／TDOA定位示意图。在用户和基站通信时要求用户上报系统帧号时间差SFN-SFN［10］，当主基站获得SFN-SFN且已知与相邻基站的定时偏移，即可获得二者的发射信号到达目标用户的时间差（TDOA）。设目标用户信号到达主基站（为目标用户服务的基站）和相邻基站i的时间之差为Δti，目标用户信号到达主基站的时间为tb，到达相邻基站i的时间为ti，则TDOA为：Δti＝ti－tb。目标用户接收到该基站下行信号后，延迟T0向基站发射信号［9］，定位台分别截获基站下行信号和目标用户上行信号的接收时刻，即可测得其接收基站信号与接收目标用户信号的时间差Δt。定义τx为目标用户信号到达定位台的传播时间，τy为基站信号到达目标用户的传播时间，τz为基站信号到达定位台的传播时间，设基站发射信号的起始时刻t0，则有Δt＝（t0

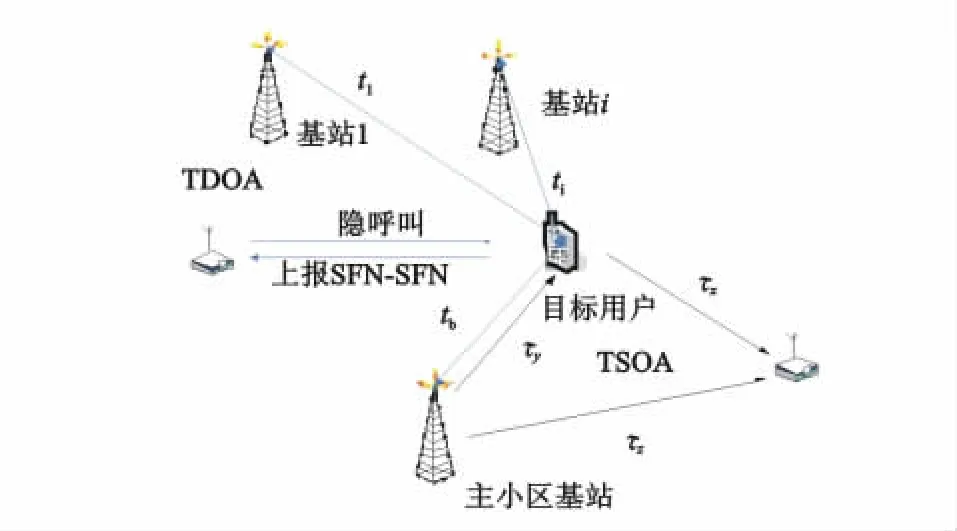
图1 TSOA／TDOA定位原理示意图Fig.1 Theory of TSOA／TDOA locating

1.2 UKF算法原理

UKF算法是一种递归式贝叶斯估计方法，它用一组确定的取样点来近似后验概率，但是UKF算法不必线性化非线性状态方程或测量方程，能直接利用非线性状态方程来估计状态向量的概率密度函数，一定程度上避免了EKF线性化过程中忽略高阶项带来的误差问题。UKF算法精度可达到二阶甚至更高阶，在非线性系统中可以获得优于EKF算法的滤波效果。

UKF算法步骤如下所述：

1）初始化，

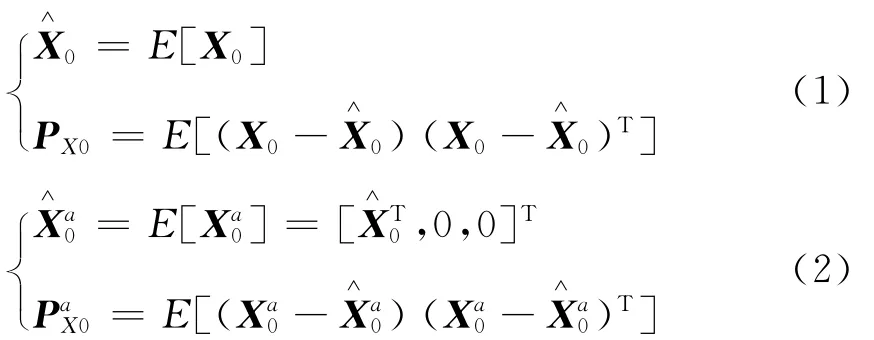
式中，Xα＝［XTWTVT］T是由状态变量X过程噪声W和观测噪声V扩展成的新增广状态向量。

2）对于k＝1，2，3，…，实现以下步骤：

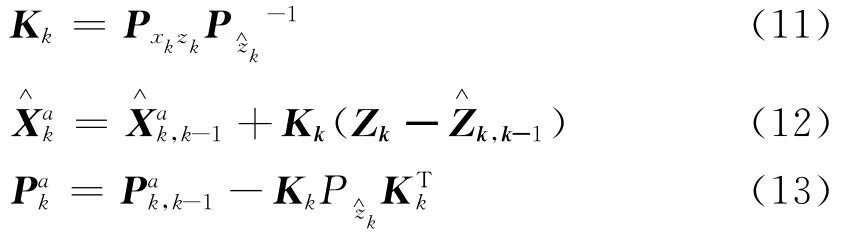
3）计算权值和参数

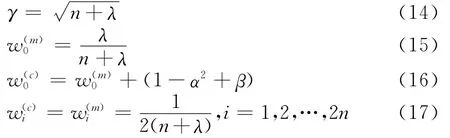
式中，λ＝α2（n＋k）－n；n为增广状态向量的维数；α为决定Sig ma点分布广度的主要刻度因子，其典型分布范围为10－3＜α≤1；β是零阶Sig ma点权值的第二刻度因子，用来强调验后协方差计算；k为第三刻度因子，通常设置为0。

2 基于TSOA／TDOA模型的UKF算法

本节在上一节对TSOA／TDOA定位和UKF算法原理的分析的基础上，利用获得的TSOA与TDOA信息，应用UKF算法对目标移动台实施跟踪。对于上述非线性定位跟踪问题，应该首先建立其状态方程和观测方程。

2.1 基于TSOA／TDOA的UKF观测方程

假设定位台获取TSOA和TDOA测量值分别为τk和 Δtk。它们分别由式（18）、式（19）得到：

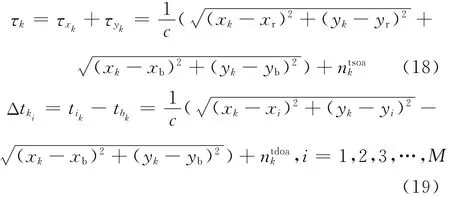
式中，τk为k时刻系统TSOA测量时间，Δtki为k时刻目标用户到主基站和到相邻基站的时间之差，M为参与计算的相邻小区的数目，（xk，yk）为k时刻目标移动台坐标，（xb，yb）为主基站（目标用户所在小区基站）的坐标，（xi，yi）为相邻基站的坐标，（xr，yr）为侦收台的坐标，c为光速，ntsoak∈ N（0，TDOA测量噪声，并且相互独立。将k时刻的测量值表示为zk＝ ［τk，tk1，tk2，…，tkM］T，测量等式可以表示为动态模型形式，即UKF观测方程为：

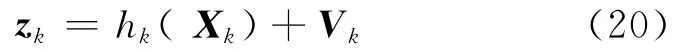
式（20）中，Vk∈ ［是系统的观测噪声，它的协方差矩阵记为R＝diag（I）。

2.2 基于TSOA／TDOA的UKF状态模型

当目标在短时间内，加速度不是很大，或者测量时间较短，我们可以认为目标在这段时间内是近似匀速运动，但在横向和纵向上均受到随机加速影响［12］。在移动台定位应用中，目标用户处于市区或者郊区，运动速度不是很高，认为目标移动台的运动状态为受到随机加速影响的匀速运动是合理的。

根据以上分析建立受到随机加速影响的UKF匀速运动状态模型。假设移动台在二维平面上运动，k 时刻的运动状态为 Xk＝ ［xk，yk，vxk，vyk］T，（xk，yk）为k时刻移动台的坐标位置，（vxk，vyk）分别为k时刻移动台在x轴和y轴方向的速度分量，由此，系统的状态模型可以表示为：

式（21）中，k时刻即t＝t0＋k Ts时刻，Ts为抽样间隔。Wk＝ ［］T为k 时刻系统的过程噪声，表示该时刻的加速度向量，它的协方差矩阵记为Q 。将式（4）写成矩阵形式，即系统状态方程：

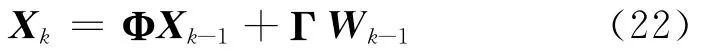
2.3 UKF算法跟踪实现

建立状态模型、观测方程后，利用UKF算法完成对目标移动台的定位跟踪，其具体实现步骤如下：

2）执行式（14）—式（17），完成算法的参数设置。

3）反复执行式（3）—式（13），完成滤波更新过程，其中式（4）、式（7）中的函数分别由式（22）、式（20）确定，直至算法结束。

3 仿真结果与讨论

为了验证UKF算法在TSOA／TDOA移动台单站跟踪系统中的应用效果，在典型蜂窝式基站分布的环境下进行仿真，在直角坐标系下分别使用EKF和UKF算法对目标移动台进行跟踪。仿真条件设置为：目标初始位置（200，100），相邻基站的坐标为：BS1（2 250，1 299），BS2（2 250，－1 299），BS3（0，－2 598），主基站的坐标为：BSb（0，0），侦察台的坐标为：BSr（450，－200），运动状态为带有随机加速的匀速运动，横向和纵向速度分别为7 m／s、2 m／s，它们均受到零均值方差为3／2的高斯随机加速的影响。抽样间隔为2 s，取100个采样点，σtsoa＝100 m，σtdoa＝50 m，α＝0.1，β＝2，k＝0。在上述仿真条件下，经过100次蒙特卡罗仿真，得到EKF和UKF算法的目标跟踪轨迹曲线及误差曲线，如图2、图3所示。

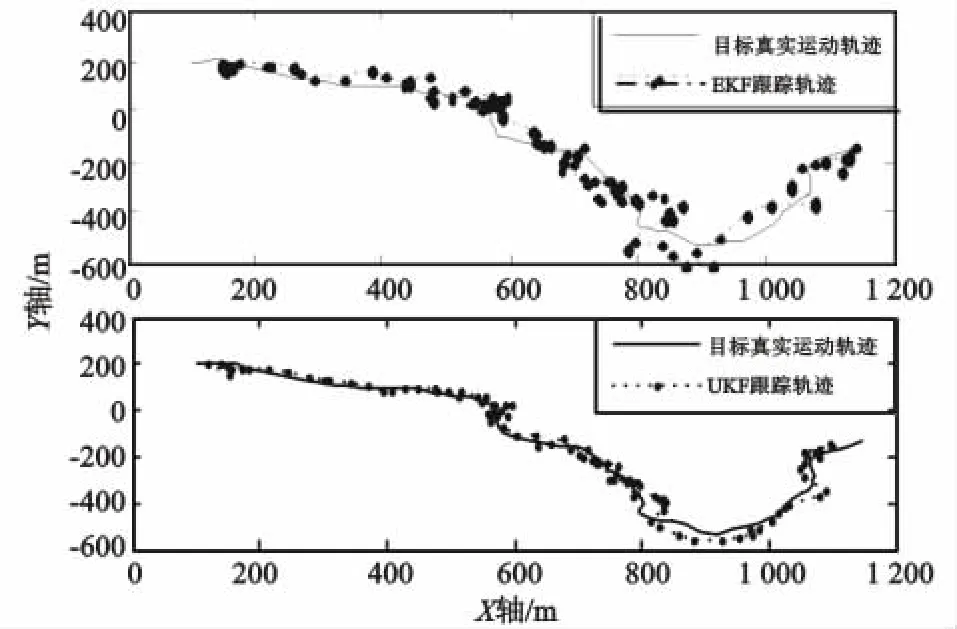
图2 一次EKF、UKF算法跟踪对比图Fig.2 Cartogram of EKF and UKF tracking

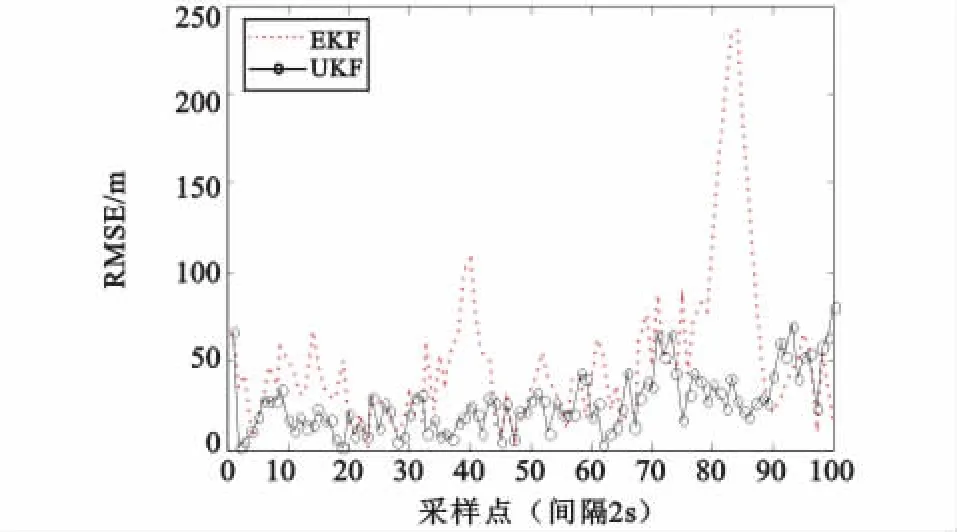
图3 RMSE比较图Fig.3 Cartogram of RMSE

由图2可看出，在轨迹较平缓的区域，两种算法都能实现跟踪，但UKF算法跟踪效果明显优于EKF算法；在目标出现机动转弯时，EKF算法出现跟踪轨迹与目标轨迹发生较严重偏离的现象，甚至在某些机动转弯较强区域出现跟踪丢失，但UKF算法能一直保持较好的跟踪效果。

图3为进行100次蒙特卡罗仿真统计得到的RMSE，其中

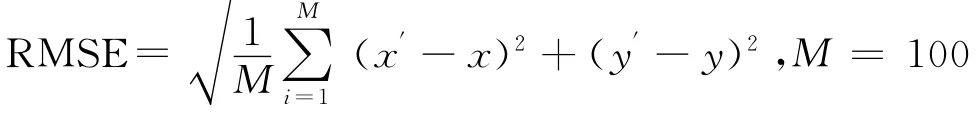
为蒙特卡罗仿真次数，（x，y）为目标实际坐标，（x′，y′）为算法估计坐标。从图中易对EKF，UKF算法的性能有更直观地了解。当到达目标机动转弯段时，EKF算法的跟踪误差迅速增大，而UKF算法的跟踪误差基本保持平稳略有增大，这与图2所示的情况也是相一致的。出现这种情况是由于EKF算法在对非线性测量方程的线性化时产生了误差，而这种误差对于上一时刻状态初值较为敏感，导致该算法对于前后状态变化较大的情况效果下降甚至滤波发散。而UKF算法直接利用系统非线性方程，无需线性化，利用一系列的确定性采样点描述滤波过程的真实均值和方差，在一定程度上避免EKF线性化方程过程中带来的误差，其稳定性和精确性更优［13］。

图4、图5为两种算法对目标速度的跟踪性能。

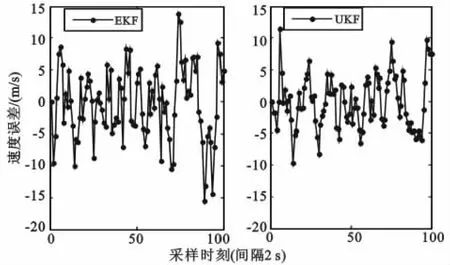
图4 X方向速度跟踪误差比较图Fig.4 Cartogram of tracking error in X direction

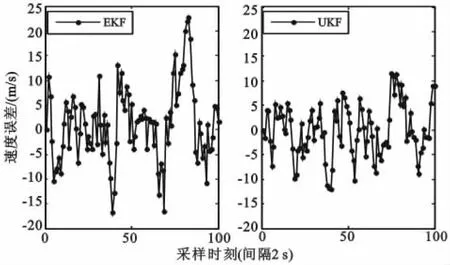
图5 Y方向速度跟踪误差比较图Fig.5 Cartogram of tracking error in Y direction

由图可知：在X和Y方向上EKF算法速度跟踪偏差在 （－15，15）范围内波动且波动的幅度较大，而UKF算法速度跟踪偏差的波动范围和幅度都要明显小于EKF算法，其对目标速度的跟踪性能更佳。

为进一步验证算法在不同速度下的跟踪性能，在上述仿真的条件下，分别以3 k m／h、30 k m／h、60 k m／h、120 k m／h的速度沿x轴方向作匀速直线运动，统计得到不同速度下位移和速度的估计误差如表1、表2所示。

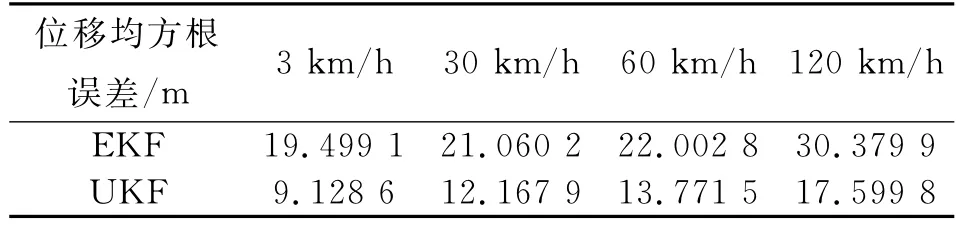
表1 不同速度下的位移均方根误差Tab.1 The locating error with different speed

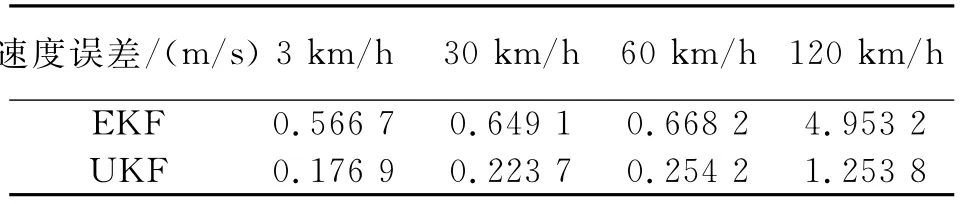
表2 不同速度下的速度估计误差Tab.2 The speed error with different speed

从表1、表2易看出，在对目标位移和速度的跟踪估计中，UKF算法较EKF算法更加精确。在速度小于等于60 k m／h时，两种算法的估计误差都随速度的增加而增大，但增加的幅度较小，相对稳定；在目标速度达到120 k m／h时，误差快速增大，但UKF算法较EKF算法的误差增加幅度更小，说明其稳定性更佳。

4 结论

本文提出一种基于TSOA／TDOA混合被动单站定位模型的无迹卡尔曼滤波跟踪算法。该算法引入TSOA／TDOA 观 测 模 式，以 观 测 的 TSOA／TDOA的有噪信息为基础，使用受随机加速影响的匀速运动状态作为跟踪算法的状态模型，将UKF算法应用在移动台的定位跟踪上，实现了对移动台的位移和速度的同步跟踪。仿真实验结果表明：使用UKF算法对目标位置和速度的跟踪效果优于EKF算法，基于TSOA／TDOA混合被动定位模型的无迹卡尔曼滤波跟踪具有良好的准确性和鲁棒性。

［1］范志平，邓平，刘林.蜂窝网无线定位［M］.北京：电子工业出版社，2002：52-100.

［2］3GPP Office.3GPP TS 25.215 v6.0.0.Physical layer-Measurements（FDD）［S］.France：3GPP，2003.

［3］邓平，朱中梁.一种天线阵列定位法及其仿真研究［J］.电子与信息学报，2005，27（6）：841-844.DENG Ping，ZHU Zhongliang.An antenna array location method and its si mulation study［J］.Jour nal of Electronics＆Infor mation Technology，2005，27（6）：841-844.

［4］Aidala V，Hammel S E.Utilization of modified polar coor dinates f or bearings-only tracking ［J］.IEEE Transactions on Auto matic Control，1983，28（3）：283 -294.

［5］Si mon Julier，Jeffrey Uhl mann，Hugh F Durrant-Whyte.A new method for the nonlinear transfor mation of means and covariances in filters and esti mators［C］／／IEEE Transactions on Auto matic Control，USA：IEEE Press，2000：477-482.

［6］Banani S A，MasnadiShirazi M A.A new version of unscented Kal man filter［C］／／Proceedings of the World A-cademy of Science，Engineering and Technology.Barcelona，Spain，2007：192 -197.

［7］赵鹤，王喆垚.基于UKF的 MEMS传感器姿态测量系统［J］.传感技术学报，2011，28（5）：642-646.ZHAO He，WANG Zheyao.MEMS sensors based attitude measurement system using UKF［J］.Chinese Jour nal of Sensors and Actuators，2011，28（5）：642-646.

［8］Xiong K，Chan C，Zhang H S.Detection of satellite attitude sensor faults using the UKF［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，43（2）：480-491.

［9］Ar ulampalam S，Maskell S，Gordon N，et al.A tutorial onparticle filters for online non-linear／non-Gaussian Bayesiantracking［J］.IEEE Transactions on Signal Processing，2002，50 （2）：174 -188

［10］胡浩，李婧，陈乐然，WCDMA系统中基于UE测量报告的无线定位及参数提取方法［J］.信息工程大学学报，2008，9（2）：200-202.HU Hao，LI Jing，CHEN Leran.Radio positioning and parameters getting method based on measurement report of UE in WCDMA system［J］.Journal of Inf or mation Engineering University，2008，9（2）：200-202.

［11］3 GPP Office.3 GPP TS 25.211 v6.0.0.Physical channels and mapping of transport channels onto physical channels（FDD）［S］.France：3GPP，2003.

［12］Eli Brooker.Tracking and Kal man filtering made easy［M］.New Yor k：Wiley，1998.

［13］王向磊，丁硕 ，苏牡丹.EKF／UKF在基于地磁场的卫星自主定轨中的应用比较［J］.测绘科学技术学报，2011，28（1）：50-53.WANG Xianglei，DING Shuo，SU Mudan.Co mpare on the application of EKF／UKF in satellite autono mous or bit deter mination using geo magnetic field［J］.Jour nal of Geomatics Science and Technology，2011，28（1）：50-53.