例析数形结合思想的综合应用

☉河南汝州市第四初级中学 怯松林

例析数形结合思想的综合应用

☉河南汝州市第四初级中学 怯松林

数形结合思想是数学中重要的思想方法，数学家华罗庚说得好：“数形结合百般好，隔离分家万事休，几何代数统一体，永远联系莫分离.”这句话说明了“数”与“形”是紧密联系的.所谓数形结合就是根据数学问题的题设和结论之间的内在联系，既分析其数量关系，又揭示其几何意义使数量关系和几何图形巧妙地结合起来，并充分地利用这种结合，探求解决问题的思路，使问题得以解决的思考方法.以下举例谈谈数形结合思想在方程、不等式、函数等方面的应用.

一、数形结合思想在方程、不等式中的应用

在平面直角坐标系内，可以借助于一次函数所对应的图像——直线，直观地解决一元一次方程、一元一次不等式组、二元一次方程组的问题，下面结合例题加以说明.

1.利用图像解一元一次方程

例1 利用函数图像解方程3x-6=0.

分析：在坐标系中先画方程所对应的一次函数y=3x-6的图像，由于解析式中函数值y就是图像上点的纵坐标y，当y=0时，对应图像上纵坐标等于0的点，也就是与x轴的交点，这个点的横坐标就是我们要求的方程的解.

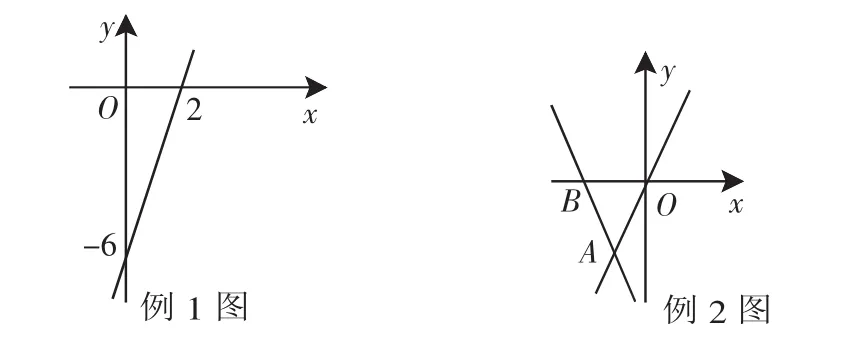
解：在坐标系中画出直线y=3x-6，如下图.

从图像可以看出直线y=3x-6与x轴交点的横坐标为2.

所以原方程的解为x=2.

2.利用图像解一元一次不等式组

例2 如上图，直线y=kx+b经过点A（-1，-2）和点B（-2，0），直线y=2x过点A，则不等式2x＜kx+b＜0的解集为（ ）.

A.x＜-2 B.-2＜x＜-1 C.-2＜x＜0 D.-1＜x＜0

解：本题直接从图像上观察，直线y=kx+b和直线y=2x的交点为A（-1，-2），确定直线y=kx+b在直线y=2x上方的范围：x＜-1.再观察直线y=kx+b的图像与x轴的交点为B（-2，0），确定此图像在x轴下方的范围：x＞-2.故选择B答案.

3.利用函数图像解方程组

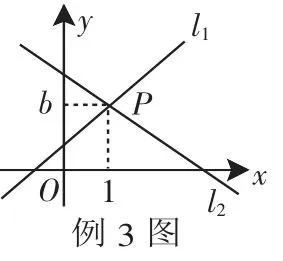
例3 如图，直线l1：y=x+1与直线l2：y=mx+n相交于点P（1，b）.（1）求b的值；

解：（1）因为（1，b）在直线y=x+1上，

所以当x=1时，b=1+1=2.

（2）如图所示，由图像知l1和l2的交点为P（1，2）.

注意：用数形结合思想解方程（组）与不等式，关键是构造它们所对应的一次函数，再利用一次函数的图像就可以说明结果.图像解法与它们的传统解法相比，往往不够方便，而且由于图像的误差常常导致求解的结果一般还不准确，但这种解法，集中体现了数形结合的思想和知识的内在联系.在日常生活中，象这种直观解决问题的方法也非常多见，它是一种很重要的能力，因此，同学们应该重视相关知识的学习，掌握这种利用数形结合思想求解问题的方法.

二、数形结合思想在函数中的应用

1.利用反比例函数图像比较大小

分析：解此题最直接的思路是将已知点的横坐标分别代入解析式，求出各个点的纵坐标再进行比较，但本题并没有给出比例系数k的取值，因而要根据函数的图像性质，确定三个点落在双曲线上的位置来确定大小.

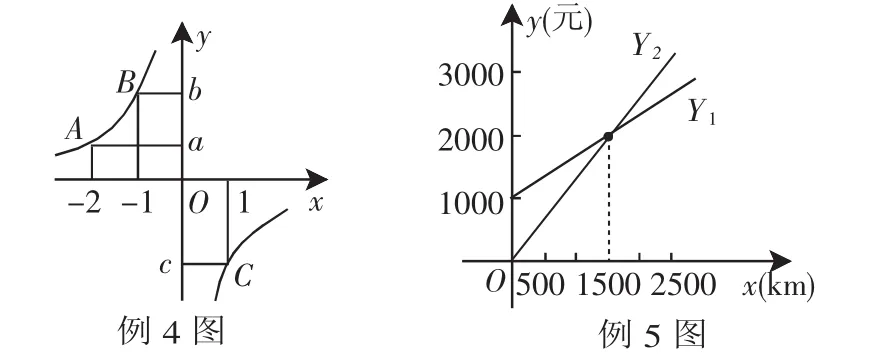
解：因为k＜0，反比例函数的图像在三、四象限，画出大致的图像，根据A、B、C三点在图像上的位置，很容易看出b＞a＞c.

2.利用一次函数图像比较租车费用

例5 某单位急需用车，但又不准备买车，他们准备和一个个体车主或一出租公司其中的一家签定月租车合同，设汽车每月行驶xkm，应付给个体车主的月费用是Y1元，应付给出租公司的月费用是Y2元，Y1、Y2分别与x之间的函数关系图像如上图，观察图像回答下列问题：

（1）每月行驶的路程在什么范围内，租公司的车合算？

（2）每月行驶的路程等于什么时，租两辆车的费用相同？

（3）如果这个单位每月行驶的路程为2300km，那么这个单位租哪家的车合算？

分析：这是一道一次函数的应用问题，数形结合的思想在本题中有很好的体现.函数图像在上方的说明它的函数值较大，反之较小，当然，两图像相交时，说明在交点处的函数值是相等的.

解：（1）由图像可知，直线Y2的图像在直线Y1的图像下方的范围是：0＜x＜1500，所以每月行驶的路程在0＜x＜1500范围内，租公司的车合算

（2）直接观察图像，当每月行驶的路程等于1500时，租两辆车的费用相同.

（3）由图像可知，直线Y2的图像在直线Y1的图像上方的范围是：x＞1500，所以当每月行驶的路程为2300km，租个体车主合算

3.利用二次函数图像求系数的范围

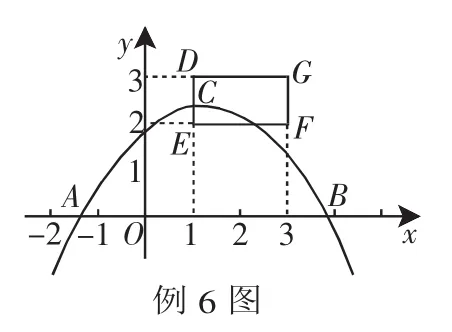
例6 如图，抛物线y=ax2+bx+c与x轴的一个交点A在点（-2，0）和（-1，0）之间（包括这两点），顶点C是矩形DEFG上（包括边界和内部）的一个动点，则a的取值范围是__________.

分析：这是一道典型的数形结合解函数型综合题，较好地体现了“以数解形、以形助数”的方法理念，正确运用二次函数的性质：增减性、对称性、最大值等.

解：仔细观察图像，a的取值范围分两种情况讨论：

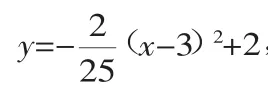
4.利用二次函数图像解综合试题

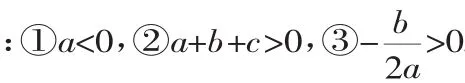
分析：仔细观察抛物线的位置走向、关键点的位置坐标，以及解析式中各个系数与图形性质的对应关系，再做出相应的判断.

解：①由图像开口方向可知，a＜0.

②因为抛物线经过点（-1，0），由抛物线的对称性可知，当x＝1时，有y＞0，即有a+b+c＞0.

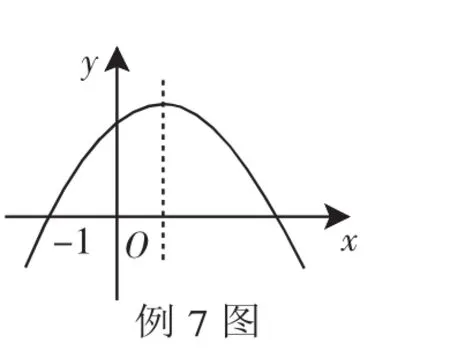
故正确的结论是①②③.

例8 如图，点G、D、C在直线a上，点E、F、A、B在直线b上，若a∥b，Rt△GEF从如图所示的位置出发，沿直线b向右匀速运动，直到EG与BC重合.运动过程中△GEF与矩形ABCD 重合部分的面积（S）随时间（t）变化的图像大致是（ ）.

解：这是一道综合性很强的识图题，要分析动态△GEF与矩形ABCD重合的各种情况.①有的考生错选A，没有考虑从出发到F点与A点重合，这时间段重合部分面积S为0；②从F点与A点重合，直到EG与AD重合，重合部分为三角形，此三角形与△GEF相似，可以用t来表示重合三角形的边长，从而求出面积S应为关于t的二次函数，且开口向上；③继续沿直线b向右匀速运动，直到EG与BC重合，运动过程中△GEF与矩形重合部分为直角梯形，同样可以用t表示直角梯形的边长，求出面积S为关于t的二次函数，且开口向下.综合观察，整个变化过程中面积（S）随时间（t）变化的图像大致是B答案.