基于合作博弈托盘租赁联盟收益分配的研究

李 晓，金寿松，冯定忠，李晓杰

（浙江工业大学 机械工程学院，浙江 杭州 310032）

基于合作博弈托盘租赁联盟收益分配的研究

李 晓，金寿松，冯定忠，李晓杰

（浙江工业大学 机械工程学院，浙江 杭州 310032）

在研究国内外相关研究现状的基础上，针对托盘租赁企业联盟情况下的分配问题进行分配策略研究.笔者通过引入Shapley值构造原理及AHP分析法，在分析托盘租赁联盟收益组成及盟员风险承担能力的同时，提出了基于可量化收益、不可量化收益及风险承担能力的收益分配模型，此种分配方案是实现个体理性与群体理性的保障，是联盟保持稳定的必要条件.最后通过算例分析，验证了这种分配方法的合理性.

托盘租赁；联盟；收益分配；博弈论

托盘租赁是现代服务业的一种新业态，由于全球托盘租赁业的迅速发展以及其蕴藏的巨大发展潜力，我国已经把托盘租赁行业作为发展经济的一个新增长点.但是我国的托盘租赁企业还不够规范，没有形成一定的规模，不能满足市场的需求，所以建立托盘租赁联盟迫在眉睫.托盘租赁战略联盟是托盘联营的一种特殊形式，它是基于我国现阶段托盘租赁公司在全国的发展情况，为迅速组建中国托盘联营系统，并尽快实现全国范围内的物流托盘化作业，而提出的一种联营组建方式.所谓战略联盟是指“以信息、通信技术为主要手段，迅速实现资源有效集成，而进行的企业核心能力的一种外部整合，其目的在于迎合快速变化的市场机遇”［1］.在这个战略联盟中每一个成员都为联盟贡献出自己的核心能力，并相互连接实现资源共享和费用分担，以把握迅速变化的商机，实现最终双赢的目的.

托盘租赁战略联盟本质上就是为追求更高经济利益而形成的合作关系，利益是各个盟员相互合作的基础.因此建立一个公平、合理的利益分配机制是托盘租赁战略联盟可持续发展的前提.国内外相关学者关于联盟利益分配的方案研究成果可以分为3类：一是借助投资评估理论建立了基于投资额的利益分配方案［2］.二是在收益分配契约的基础上运用对策理论建立联盟收益的博弈分配模型，主要是通过采用Shapley值法解决盟员之间的利益分配问题［3］.三是运用风险评估理论提出的基于承担风险大小的协商模型和加权重心模型［4］.以上的收益分配都只是对联盟产生的可量化收益的分配，忽略了不可量化收益及各盟员承担风险的不同带来的收益波动，这部分收益不能通过公司会计进行核算，但它们的存在对联盟的稳定发展有着极其重要的意义.基于此笔者试图提出将不可量化收益、风险承担能力考虑在内的联盟收益分配模型，使联盟收益分配更加合理、更加符合实际.

1 利益分配原则的博弈分析

托盘租赁企业的战略联盟是一种互补性合作，彼此拥有对方所不具备的特质资源来获得超额利润，因为这种超额利润是各个盟员共同努力的结果，这就要求盟员能根据各自的贡献来分享它.

设托盘租赁企业集合为N＝｛1，2，…，n｝，则任意S⊆N，称S为N的一个联盟.特殊情况，允许取S＝φ和S＝N，φ表示空集即子联盟S中成员个数为0，N表示全集即子联盟S中成员个数为n，若｜N｜＝n则N中联盟个数为2n.

设v（S）是定义在N 一切子集上的实函数［5］，其满足

（N，v）为n个人的联盟博弈，v（S）为博弈的特征函数.其表示联盟S通过协调其成员策略所保证得到的最大利益.假定用一个n维向量x＝（x1，x2，…，xn）∈Rn来表示盟员的收益分配，其中xi表示第i个托盘租赁企业所得份额.

联盟要存在必须满足以下条件：

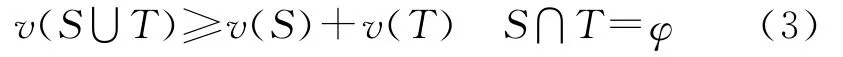
这是联盟存在的必要条件，联盟的总收益要大于不联盟时各个个体收益的总和.

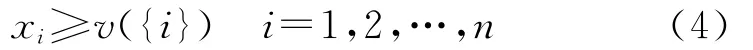
托盘租赁企业i如果加入到联盟中后获得的收益大于未加入之前，符合个体理性条件.

联盟中的收益完全分配给各个盟员，符合群体合理性条件.若以上条件都成立我们就称x＝（x1，x2，…，xn）为联盟的一个分配，分配的全体用E（v）来表示：

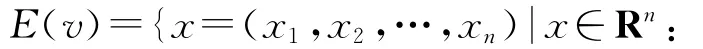
2 联盟利益分配模型

2.1 可量化收益的分配

笔者利用Shapley值模型对可量化收益进行分配，这种分配方法既不是平均分配，也不同于基于投资成本的比例分配，而是基于盟员在动态联盟经济效益产生过程中的重要程度来进行分配的一种分配方式，与其他方法相比较而言，这种方法具有一定的合理性和优越性［6］.

式中：φi（v）′为在合作中第i个成员所得到的收益；｜s｜为子集S 中元素的个数；w（｜s｜）为加权因子，n为集合N 中元素的个数.v（s）为子集S的效益；v（s＼｛i｝）是子集S中除去企业i后可取得的收益.

2.2 基于不可量化收益的分配修正算法

通过前面的分析知道Shapley值在可量化的收益分配中是一个很不错的解决方案，下面利用Shapley值的构造原理［7］来求不可量化收益在各个盟员之间的分配比例.

首先定量化动态联盟（N，V，U），假设U中共有k项元素，即联盟合作最多有k项不能度量的收益，用一个k维向量Uk＝（J，…，J）来表示.类似的V成为2N上的一个映射，V：2N→RK，对于N的任意一个子集S是一个联盟，联盟收益v（S）是一个k维向量，其每一个分量取值为0或1，若第j个分量取值为1，则表示该次合作得到了U中的第j个元素，取值为0就表示没有得到该项元素，令v（φ）＝（0，…，0）.用Ek表示动态联盟（N，V，U）的全体，则寻求的动态联盟的解f是一个映射：Ek∈（Rk）n，其中fj（V）是一个k维向量.

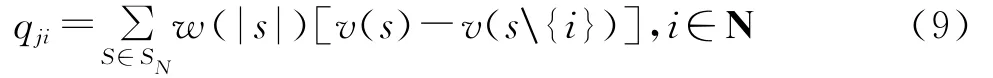
对任意的动态联盟（N，V，U）∈EK，其定量解为qji中的每个分量表示第i个参与人分享u中相应元素的比例或者份额.

基于不可度量收益分配的修正算法为

φi（v）″表示第i个企业基于对不可度量收益的贡献在原来收益的基础上进行调整的份额，v（N）为联盟的总体收益.

rj为k项不可度量收益之间重要性比例，通过专家打分法来确定.为了克服每个专家对不可度量收益评价时计分不一致，导致选择结果没有可比性的问题，笔者事先确定评分标准，如表1所示.

表1 评价等级Table 1 Evaluation scale

2.3 基于风险因素的收益分配修正算法

采用层次分析法对盟员所承担的风险进行定量分析，将各种风险量化为具体的权重指标对分配方案进行修正.用层次分析法对非定量事件进行定量分析这方面的文献比较多，这里就不做讨论了.我们主要研究如何利用风险因子去修正Shapley值法利益分配模型.

在Shapley值法利益分配模型中盟员的经营风险是均等的，即联盟N＝｛1，2，…，n｝中的每个成员承担风险，显然这是一种理想情况．笔者为克服这种分配缺陷，采用AHP确定风险因子对收益分配进行修正，其算法为

2.4 收益分配模型

将可量化收益、不可量化收益及风险因子都考虑在内的收益分配模型为

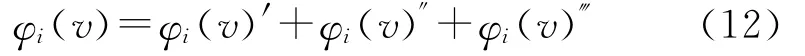
式中：φi（v）为第i个盟员企业获得的实际收益；φi（v）′为第i个盟员企业可量化收益的分配额；φi（v）″为第i个企业基于对不可度量收益的贡献在原来收益的基础上进行调整的份额；φi（v）‴为第i个企业基于承担风险的差异在原来收益基础上进行调整的份额.

3 实例验证

有三家托盘租赁企业，若单干每年可分别获利20，30，15万元，若1，2两家联营可获利60万元，1，3两家联营可获利40万元，2，3两家联营可获利65万元，若三家都联合在一起，则联盟每年的收益增至100万元.企业1拥有基于RFID技术的托盘追踪管理系统，而企业2租赁网点多，分布范围广.企业1，2联营不仅扩大了托盘租赁网点的分布范围，而且通过对托盘实时追踪和可视化管理使托盘的异地交换更加快捷方便，进一步提高托盘租赁的服务质量和顾客的满意度.通过三家企业的整合，使得联盟占有了更大的租赁市场，并创立了联盟的品牌，使得整个联盟在托盘租赁行业更有影响力.

如果将联盟所得利润进行均分，每个企业可得33.3万元.但是这种分配方案是不能调动各个盟员积极性的，甚至有的盟员可能产生偷懒、懈怠的现象.在这种情况下，我们尝试用上文中所列模型进行收益分配.

3.1 可量化收益的分配

将三家托盘租赁企业的联盟记为N＝｛1，2，3｝，并记各自独立经营获利v（1）＝20万元，v（2）＝30万元，v（3）＝15万元，由企业1参加的所有合作形式的集合S1＝｛1，1∪2，1∪3，1∪2∪3｝.由题意得v（1∪2）＝60，v（1∪3）＝40，v（1∪2∪3）＝100.按照Shapley值法求φ（v）的值，联盟成员企业1的分配利益φ1（v）的计算，如表2所示.

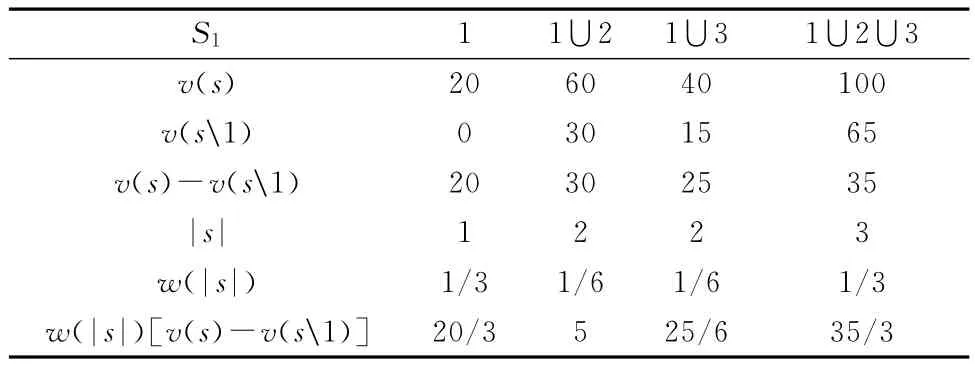
表2 企业1的利益分配计算表Tabale 2 Profit distribution table of enterprise 1

将表格最后一行相加得φ1（v）′＝165／6万元，同理可得φ2（v）′＝45万元，φ3（v）′＝165／6万元.也就是说通过Shapley值法进行利益分配，三家企业可分别获得27.5，45，27.5万元.

3.2 基于不可量化收益的分配修正算法

分析上例我们可以看出通过这三家托盘租赁企业联营可以产生三项不可度量的收益：服务能力、市场机会、联盟品牌.其中服务能力这项收益是通过企业1和企业2的联合实现托盘实时追踪和可视化管理，使托盘的异地交换更加快捷方便，提高托盘租赁的服务质量和顾客的满意度而产生的.

1）动态联盟成员的集合N＝｛1，2，3｝.

2）特征函数V 满足：V（N）＝｛服务能力，市场机会，联盟品牌｝；V（1）＝V（2）＝V（3）＝0，V（1，2）＝｛服务能力｝，V（2，3）＝V（1，3）＝0.

3）边际值解为q1＝｛服务能力，市场机会，联盟品牌｝，q2＝｛服务能力，市场机会，联盟品牌｝，q3＝｛市场机会，联盟品牌｝.

4）边际值量化：u＝（1，1，1），V（｛1，2，3｝）＝（1，1，1），V（｛1｝）＝ V（｛2｝）＝ V（｛3｝）＝0，V（｛1，2｝）＝（1，0，0），V（｛1，3｝）＝V（｛2，3｝）＝0.

5）根据式（9）计算得

通过专家打分法求得3项不可度量收益之间的比例关系rj为r1＝0.5，r2＝0.4，r3＝0.1.根据式（10）可得：φ1（v）″＝8.33万元，φ2（v）″＝8.33万元，φ3（v）″＝－16.66万元.

3.3 基于风险因素的收益分配修正算法

通过AHP法求的三企业各自的风险因子分别为R1＝0.2，R2＝0.3，R3＝0.5.根据式（11）可得：φ1（v）‴＝ －13.33 万 元，φ2（v）‴＝ －3.33 万 元，φ3（v）‴＝16.66万元.

3.4 联盟收益分配

根据式（12）可以求出φ1（v）＝22.5万元，φ2（v）＝50万元，φ3（v）＝27.5万元.

实例验证，φ1（v）＋φ2（v）＋φ3（v）＝100万元，且φ1（v），φ2（v），φ3（v）均大于单干时各自所获得的收益，并且φ1（v）＋φ2（v）＞60万元，φ1（v）＋φ3（v）＞40万元，φ2（v）＋φ3（v）＞65万元.因此，三家合作所得到的效益比单独一家或是任意两家合作得到的效益要多，于是三家加入联盟的积极性比较高，联盟的稳定性也比较好.

4 结 论

笔者基于各企业在联盟中的重要程度利用Shapley值法对联盟中的可量化收益进行分配，并充分考虑各盟员对不可量化收益的贡献，及盟员间因承担风险的不同带来收益波动这两个因素，并提出相应的修正方案，使联盟能够避免平均分配、吃大锅饭现象发生，使分配更加合理、更加符合实际.笔者所研究的分配方案为事后分配，但在很多情况下需要对未来合作收益情况进行合理的预测，制定初步方案，然后根据合作过程中伙伴对于方案的满意度及伙伴的贡献程度做适当的调整，也就是将事前分配和事后分配相结合，综合运用制定分配方案，限于篇幅这部分内容在此不再展开讨论.

［1］韩臻聪.论物流企业战略联盟的建立［J］.现代管理科学，2003（9）：55-58.

［2］冯蔚东，陈剑.虚拟企业中伙伴收益分配比例的确定［J］.系统工程理论与实践，2002（4）：45-50.

［3］戴建华，薛恒新.基于Shapley值法的动态联盟伙伴企业利益分配策略［J］.中国管理科学，2004，12（4）：33-36.

［4］叶飞.虚拟企业利益分配新方法研究［J］.工业工程与管理，2003，8（6）：44-47.

［5］HAMIACHE G.A mean value for games with communication structures［J］.International Journal of Game Theory，2003（23）：533-544.

［6］张青山，郑国用，赵忠华.虚拟企业风险分析模型［J］.工业技术经济，2001（1）：37-38.

［7］刘德铭，对策论及其应用［M］.长沙：国防科技大学出版社，1994.

Research on the benefit distribution of pallet rental alliance based on game theory

LI Xiao，JIN Shou-song，FENG Ding-zhong，LI Xiao-jie
（College of Mechanical Engineering，Zhejiang University of Technology，Hangzhou 310032，China）

On the basis of related research of domestic and abroad，profit distribution program of pallet rental enterprise under alliance condition is studied.The shapley value method and AHP method are introduced to construct the income distribution program on the basis of analyzing income component of pallet rental enterprise alliance and the ability of the risk undertaken.The program can assure the realization of both individual and group rationality and stabilization of pallet rental alliance.Finally，the rationality of the program is verified by a numerical example.

pallet rental；alliance；income distribution；game theory

F252.1

A

1006-4303（2012）01-0084-04

2010-09-21

浙江省自然科学基金资助项目（Y606271）

李 晓（1986—），女，山东济南人，硕士研究生，主要从事工业工程、物流工程和企业信息化研究，E-mail：lixiaomoon＠163.com.

（

陈石平）