节点法与改进节点法的讨论

2012-08-23袁韬，冯平，杨静，葛敏

电气电子教学学报 2012年1期

袁韬，冯平，杨静，葛敏

(后勤工程学院机械电气工程系，重庆 400082)

0 引言

节点电压法是电路中任一节点对参考节点的电位为独立的变量的一种分析方法，若电路中有几个节点利用KCL方程列出(n－1)个独立方程求出相应节点对参考节点的电位，然后求出各支路元件的电压及电流等电量。

电路是由元器件与导线连接的实体，计算机所能分析的是数学方程。如果想使用计算分析电路，需要先将实体电路建模成为支路组成的网络模型，再采用适当的分析方法由网络模型构建数学方程。这种分析法主要有节点法、改进节点法、混合分析法和稀疏表格法四种，在这里选择适用范围较广的改进节点法(MNA)进行分析［1］。

1 节点电压法(NA)

假设待分析的电路中有n个节点、b条支路，那么取n－1个非参考节点电压Un作为未知的电路变量，则可写出NA 方程:

建立节点方程的关键是形成节点导纳矩阵Y和等效电流源向量J。在建立方程的过程中，首先要为待求电路的支路和节点编号，且最后一个节点号为参考节点。画出相应的拓扑图。节点电压方程的形成方法有表单形成法和矩阵计算法两种。

1)表单法形成节点方程

表单形成法是将非理想电压源支路通过电源等效变换为电导与理想电流源并联，每个元件为一条支路，根据支路方程直接形成矩阵Y和向量J的相应元素。这种方法仅能分析包含电阻、电导、电流源、电压控制电流源以及电流控制电流源(其中，控制支路为电阻或电导支路)。

2)矩阵计算法形成节点方程

矩阵计算法是在构建节点支路关联矩阵A、支路导纳矩阵Yb、电流源向量Is、电压源相量Us的基础上，通过矩阵运算求得节点电压方程的稀疏矩阵及右端项矩阵Y和向量J。

比较上述两种形成基本节点电压方程的方法可见，表单法只需考虑按关联参考方向给定的单个元件的支路特性，一旦程序编好，只需给出“支路号、元件属性、起始节点号、终止节点号、元件值、控制支路号”信息就能自动形成方程，而且所形成的代数方程组阶数为n－1，往往远小于支路数。而矩阵计算法则需要人工准备A、Yb、Is和Us，且与参考支路有关。另外，矩阵计算法中A和Yb是非零元素很少的稀疏矩阵，用满阵处理时既费存储量又费计算时间，很不经济。这些对于计算实际的大规模电路是不合适的。基本节点电压法NA也可以计算非理想受控电压源，但是，需要先对电源进行变换，而且，他们在YUn=J矩阵中的数值已经不是元件本身的值，规律十分复杂。

基本节点电压法还有一个致命的缺陷，那就是无法计算含有理想电压源的电路。而改进的节点电压法正是针对这一问题而提出的。

2 改进的节点电压法(MNA)

假设待分析的电路中有n个节点、b条支路，其中有bv条理想电压源支路，包括电流源控制支路。那么，取n－1个非参考节点电压Vn和bv个电压定义支路的电流Iv作为未知的电路变量。这样列写出来的方程称为改进的节点电压方程，它保留了方程阶数低的优点，而且克服了基本节点法不能直接处理理想电压源支路、阻抗为零支路以及流控器件的缺点。因此，改进的节点电压法得到了广泛的应用，改进的节点电压法将元件分为三类:第一类:用导纳描述的元件。这些元件只需选节点电位作为方程变量;第二类:不用导纳描述的元件，如独立电压源、受控电压源。此外，还包括那些需要支路电流作为输出变量的元件，如电感、互感元件等;第三类:独立电流源。

3 含有无伴电压源的电路情况

3.1 含有无伴电压源和节点电压

在一个电路中含有一个无伴电压源或虽有多个无伴电压源但它们的一端接在同一节点上，那末常选择电压源的一端(公共端)为参考节点，则另一端的节点电压为电压源的电压，则不必再对该节点列出节点方程，方程数目为(n－1)节点数减少无伴电压源的数目。

3.2 无伴电压源接在两个非参数节点间

当含有无伴电压源接在两个节点之间的情况，如图1所示。可以把无伴电压源接在两个非参考节点看作广义节点［2］，他们看作一个包含电压源及其两个节点的一个封闭区，对含有广义节点的电路分析也可以用两种常见方法进行处理。

图1 电路图

(1)通常的节点电压法:即把无伴电压源中的电流作为未知量列入节点方程，同时增加一个节点电压与该无伴电压源之间的约束关系，列出一个补充方程，使未知量个数仍然与方程数相等，可解出所有的未知量。

(2)在广义节点处作为一个闭合区列出KCL方程同时再对含电压源的回路列出KCL方程，如此处理独立方程数与未知量仍为相等，同样可解出未知量［3］，对图(1)采用 KCL 分析得

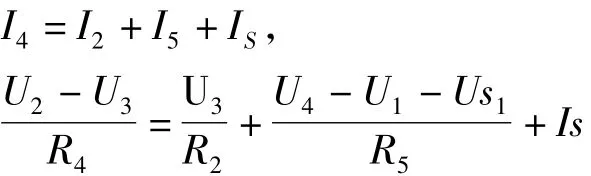
可以得到U4－U3=Us2

对节点1有U1=U2，对节点2有

可以看到，方法(1)要列出5个方程;而方法(2)要列出4个方程。

方程数目的多少直接决定所求问题的难易程度。因此，应采用尽可能少方程数目的方法，降低问题的解决难度。

按上述方法，实际上多一个无伴电压源，节点电压的数目在原有的基础上多一个，那求解方程难度增加了。

3.3 含有无伴电压源电路的简化节点电压法

(1)基本方法

这里仍以图(1)为例说明含有无伴电压源的简化节点电压法的方法。令电导Gi=1/Ri，仍选0点为参考节点，各节点电位为U1;U2;U3;U4列出各节点电压方程如下:

若求出U3，则U4便已知，故实际上U2;U3组成了一组完备的独立方程变量组:

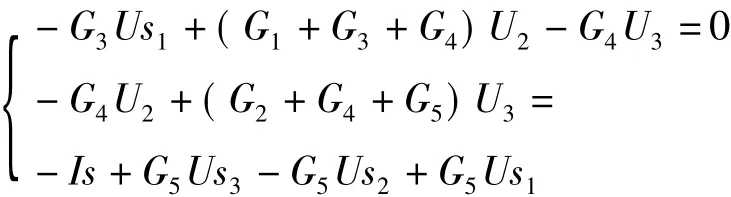
综合上述可得:GiUi=I。这里的I为流入节点的电流代数和。

由上述分析可知:电路的独立节点n=4，由于有两个无伴电压源，最终电路简化为用两个节点电压来表示的两个独立的节点电压方程组求解问题。总之，当电路有 n个独立节点和m个无伴电压源时，节点独立电压方程数目为(n－m)个，从而简化了求解方程的难度。

(2)讨论直接写出(n－m)个方程:

以节点3为例，由KCL可得:

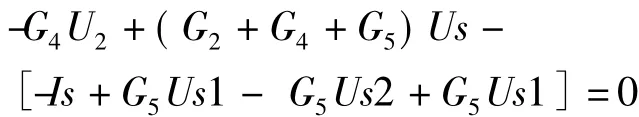
线性电路方程必须是线性方程，故有

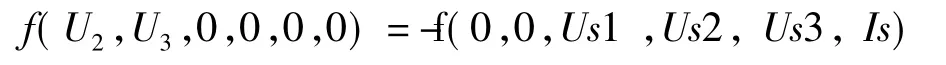
由此可得［结论］各独立电源为零时，节点电压等于流入节点的电流代数和。

现我们仍以图(1)为例，对节点2有:

对节点3有:

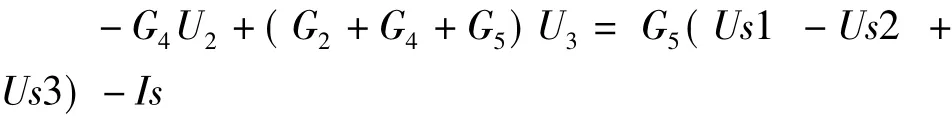
3.4 改进节点电压法

含有无伴电压源和无伴受控源电路的情况下，受控源具有电源的性质和电阻的性质，故一般情况可将受控源与独立电流一样对待，只是受控量用节点电压表示即可，因而多一个控制量方程，方程数目增多。受控源不能单独作用于电路，但当电路中有独立源时，并考虑独立源对受控源的影响，那末，受控源可像独立源一样施予电路影响，也就是具有一般电源的性质，这样改进的节点电压法同样可以推广到含有无伴受控源的电路。