三个相似三角形在教学中的作用初探

卢健康

(西北工业大学电工实验教学中心，陕西西安 710072)

0 引言

在“电工技术”中，正弦交流电路的内容无疑是最重要的一章，因为无论从理论体系还是从工程实际来讲，它都是电路分析的核心内容。而其中的RLC串联电路分析一节，则是该章的重点，可谓重中之重。该节中引出的(复)阻抗的概念，是正弦电路中最重要的概念。它不仅是描述正弦电路中任何负载元件的最基本相量模型(因为R、L、C单一元件或是RL、RC、LC这样的串联组合也都可用阻抗描述)，而且是任一无源线性二端网络化简到最简时的电路模型。作为这一节内容分析的结果，即一个阻抗上各个元件参数的关系、各部分电压电流关系及其功率关系，最后都简洁直观地浓缩在了阻抗三角形、电压三角形、功率三角形(以下简称其为“三个相似三角形”)之中。因而这三个相似三角形可谓正弦电路内容中最精彩的妙笔!然而，一般“电工技术”教材中在引出这三个相似三角形后，通常只是点出了它具有便于记忆和分析的作用，而未对其做进一步讨论。笔者在教学实践中发现，如果教师不加以强调，学生一般对它也不够重视。有鉴于此，本文对它做一些初步探讨，研究如何具体利用它分析求解电路，以便更好地用它指导学生总结该章内容和求解各种正弦电路习题。

1 三个相似三角形的图形公式描述

在RLC串联电路中，以电流为参考相量，并且规定该电路中的每个元件R、L、C上的电压及总电压的正方向均与电流正方向一致，则描述该电路的三个直角相似三角形如图1所示。下面给出其数学公式的表述。

阻抗三角形:

电压三角形:

功率三角形:

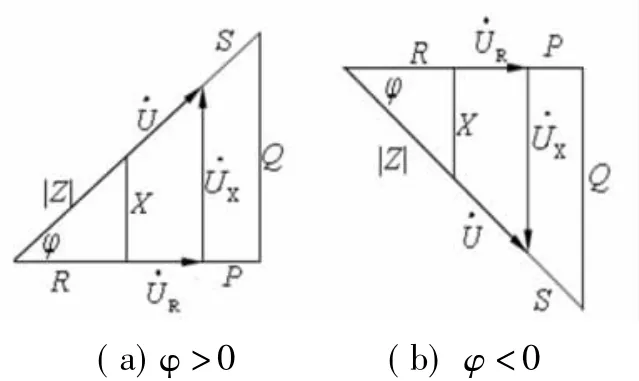
图1 阻抗三角形，电压三角形，功率三角形

三个相似三角形间关系用以下三个公式表述。

(1)阻抗三角形与电压三角形间的关系式为:

式(4)即相量形式的欧姆定律，它是分析正弦电路的最重要定律。

(2)功率三角形与电压三角形间的关系式:

(3)根据(4)式与(5)式即可推得功率三角形与阻抗三角形之间的关系式为

图1所示的三个相似三角形存在的缺陷是不能反映出阻抗Z中是否包含有电感与电容两种储能元件。如果阻抗Z中包含有这两种储能元件，则三个相似三角形只表示出了电抗(感抗与容抗之差)、电抗上的电压(电感端电压与电容端电压之差)和电路中的总无功功率(电感上的无功功率与电容上的无功功率之代数和)。因此，为了能全面表述阻抗Z中各个元件参数和各部分电压与电流及三种功率，还须补充以下几个公式。

其中，XL=ωL=2πfL，XC=1/ωL=1/2πfC

2 图1蕴含的计算公式与解题方法

如上所述，图1简洁直观地用复平面上三个相似的直角三角形，全面反映了RLC串联电路中的各个物理量和参数间的各种关系式，而学生在中学对这样的三角形的边角关系及其相关三角函数知识已经非常熟悉，再加上中学已经学过复数知识，因此，在讲授了RLC串联电路的各种电工学概念和定律之后，应该充分挖掘和利用图1中所蕴含的电路分析知识和学生中学所打下的知识基础，以便有效地指导学生掌握求解正弦电路计算题的多种方法。下面对此做详细分析。

图1的三个相似三角形共有9条边与9个角，但只有一个角(图中取为φ)能够为独立变量，再加上三个相似三角形对应边的比值，共包含有11个独立变量。它们的大小分别代表RLC串联电路中的R、X、|Z|、UR、UX、U、P、Q、S、φ 和 I这 11 个物理量(电压三角形中箭头的方向还表示了电压相量的初相位)。如果电路中包含L和C两种储能元件，则尚缺(7) ～(9)式中的 XL、XC、UL、UC、QL和 QC这 6个物理量。上述17个量加上角频率ω共18个量，就是对RLC串联电路进行正弦稳态分析的全部物理量。分析求解线性正弦稳态电路的计算题，不外乎就是已知或给定阻抗(本文不考虑导纳)上的某些量而求出其他部分或全部的量(有时还需根据相量求瞬时值，本文从略)。

下面先列出图1所蕴含的各个物理量间的关系式，即解题所需的计算公式。

每个三角形的各条边之间的平方和关系式:

阻抗角和各条边之间的三角函数关系:

三个三角形两两相似，它们的各条对应边成比例，比值等于电流有效值或其平方:

根据(14)～(16)式与(4)式还可以导出把三个三角形中的对应边联系在一起的三个常用公式:

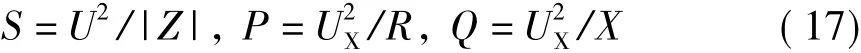
考虑到上述(10)～(17)式中每个等号即反映出一个独立的关系式，那么图1中就蕴含了24个关系式。如此众多的公式既不便于记忆也不便于在解题时迅速从中选出合适的公式套用。但熟记图1却容易得多。

3 计算题的进一步分析

如何根据图1来快速准确地分析求解计算题，下面根据平面几何的三角形与三角函数知识，做进一步分析(以下假设已知角频率ω，实际中一般也是如此)。

1)图1中的任一三角形可由其3条边和角φ(或其补角)这4个量中的任意两个量唯一决定。由此可知，如果计算题中的已知量和待求量局限于图1的一个三角形内，则必须已知全部4个量中的两个量。每个三角形已知量和待求量的不同组合共有6种。如果已知两条边求第三条边，用3条边长间的平方和关系式来求较为简单，通过三角函数关系式计算比较繁琐。其他组合情况下只能用三角函数关系式来计算待求量。

2)如果已知量和待求量不在一个三角形内，则必然涉及两个或三个三角。则至少必须已知上述全部11个物理量中的三个量，且三个量不能都全部属于一个三角形，这样才有可能确定第2个或第3个三角形。

3)为了用最便捷方法求出待求量，需要先把所有待求量按其在图1中的地位分成如下4类，然后针对其特点选取最合适的计算方法。

(1)电流有效值I，它未显示在图1中，是由相似关系间接表示出来的量。它是电路分析中最重要的物理量。只能用两个对应边的比值来求出它。

(2)阻抗角φ，它是直接显示出来的唯一一个为各三角形共有的量。根据解题需要，可以把它划归到任一三角形内。求φ的唯一方法是用一个三角形内的两条边之比求出相应的三角函数值，，然后再用反三角函数求出它。

(3) 直接显示出来的 9条边:R、X、|Z|、UR、UX、U、P、Q、S。求它们中的任一个量的步骤是:

①如果已知I和该待求边的对应边，将对应边与I或I2相乘或除即可;否则，转下一步;

②如果已知与其对应的另外两个三角形的两条边，用(11)～(13)式的对应关系来求;

③如果已知φ或其三角函数值与本三角形内的任一条边，用三角函数关系来求;

④如果已知本三角形内的另外两条边，用平方和关系式来求。

上述4步中，每一步都要求已知至少一条边，如果直接求待求量时不满足这个条件，就必须间接地来求它，即，先用上述4步中的某一步求出某个边做为中间量，然后再根据已知量与中间量求出待求量。

(4) 未包含在图1 中的量 XL、XC、UL、UC、QL和QC。如果阻抗Z中包含有两种储能元件L和C，则这6个量并未包含在图1中。它们可分为L组三个量和C组三个量。如果已知角频率和待求量所在组的元件参数L或C，则求法很简单。否则，必须已知角频率与另一组的元件参数，或者已知另一组三个量中的一个才行。在这种情况下，先利用上述方法求出与待求量单位相同的某个竖直边(X、UX或Q)，然后用(7)～(9)式求出待求量。

以上详述了阻抗Z的电路分析中全部17个量的快捷求解方法。尽管叙述起来篇幅不少，但只要对照图1，理清其中的思路，在解题时是很容易想到和做到的，因为选择这些方法的依据只是简单的三角学知识而已。

4 三角形图在后续扩展性教学的应用

利用所讲述的图1内容与解题方法，还可精简RLC串联电路内容后面的部分扩展性内容的讲授以节约课时。例如，串联谐振可以不详细讲解，因为它只是RLC串联电路当的一种特殊工作状态。此时，由于，三个相似三角形蜕变为重叠在一起的三条水平直线段，分别表示R、P和UR。在给出其 的定义后，可以让学生自己根据图1及其蜕变成的三条水平直线段，分析得出其谐振频率、电路特征。即确定9 条边和 6 个未显示量 XL、XC、UL、UC、QL、QC共15个量特定值与特殊关系，|Z|与I取最大值还是最小值等特征。

在讲授并联电容提高感性负载功率因数的内容时，通常给定ω、U、P和并联电容前后的功率因数cosφ1与cosφ2，求需要并联的电容值C。一般教材中对此的分析求解比较繁琐，也可以用图1来作如下的简化分析。

将未并联电容的电路视为阻抗Z1，并联电容后的电路等效为Z2。则Z2与Z1的无功功率之差就是电容提供的无功功率，即:

根据功率三角形的三角函数关系可知:

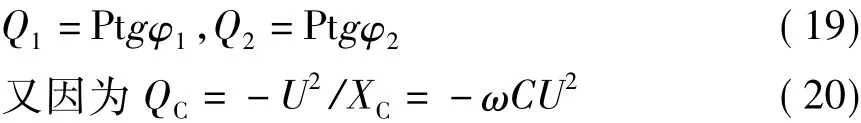
所以，由式(18)～(20)很容易得出:

如果取(19)式中的 ，电路就成为R、L串联后与C并联的谐振电路，当R、L串联电路表示一个电感线圈时，它就是教材中讲的电路。由于此时 ，根据(18)式可知Q1=－QC，因为Z1由R与L串联而成，所以根据图1很容易得出:

再根据(20)式和，即可得出求并联谐振的谐振频率的公式

可见，这里借助图1和并联谐振时电线圈与电容并联谐振容与电感的无功功率完全互补的观点分析得出公式(23)的过程要比一般教材中的分析推导简单了不少。

4 结语

本文指出了“电工技术”中RLC串联的正弦电路一节所给出的三个相似三角形在教学中的特殊地位与作用，简述了其图形与对应的公式，然后列出了三个相似三角形中蕴含的全部计算公式，详细分析了如何用它来指导求解关于阻抗Z的各种计算题目。最后介绍了如何利用它精简串联谐振、线圈与电容并联谐振和并联电容提高感性负载功率因数等扩展性教学内容的讲授。

［1］ 秦曾煌主编.电工学上册电工技术(第五版)［M］.北京:高等教育出版社.1999

［2］ 史仪凯主编.电工技术(电工学Ⅰ)(第二版)［M］.北京:科学出版社.2008