某三缸发动机悬置的优化设计

韩全友，廖 武，李玉发，赵吉刚，彭宜爱

（安徽江淮汽车股份有限公司技术中心，合肥 236001）

为响应低碳低排放的要求，小排量发动机近年来得到广泛应用，其中选择三缸小排量发动机是当前汽车行业的一个趋势。发动机是汽车上的一个主要振源，其振动由发动机经悬置系统传递到车架或车身上，尤其是三缸发动机，因为其自身的惯性力不平衡，给悬置的设计带来了更大的困难。因此，发动机悬置系统参数的设计，对于汽车整车的减振降噪来说非常重要。对于发动机悬置系统，一方面为了限制发动机运动，要求悬置系统具有较高的刚度；另一方面为了使发动机产生的振动尽可能小地传递到车身，希望悬置要足够软。所以，在悬置系统参数设计时，要兼顾这两个方面达到一致的最优解[1]。

1 优化方法

1.1 理论基础

鉴于内燃机动力总成所受激励及其作用方向的上述特点[2]，最大限度地解除动力总成一悬置系统的多自由度振动耦合，是使其具有良好隔振性能的基本方法，尤其是解除其悬置系统的侧倾自由度、垂向自由度与其他自由度之间的弹性耦合，是悬置系统设计的关键。

对于一个多缸的发动机，发动机不平衡的扰动取决于气缸的数目和布置形式。从表1可以看出，汽车上常用的几种发动机中，三缸和四缸机没有得到完全平衡。因此，对于使用这两种机型的汽车，必须特别重视悬置系统的设计。

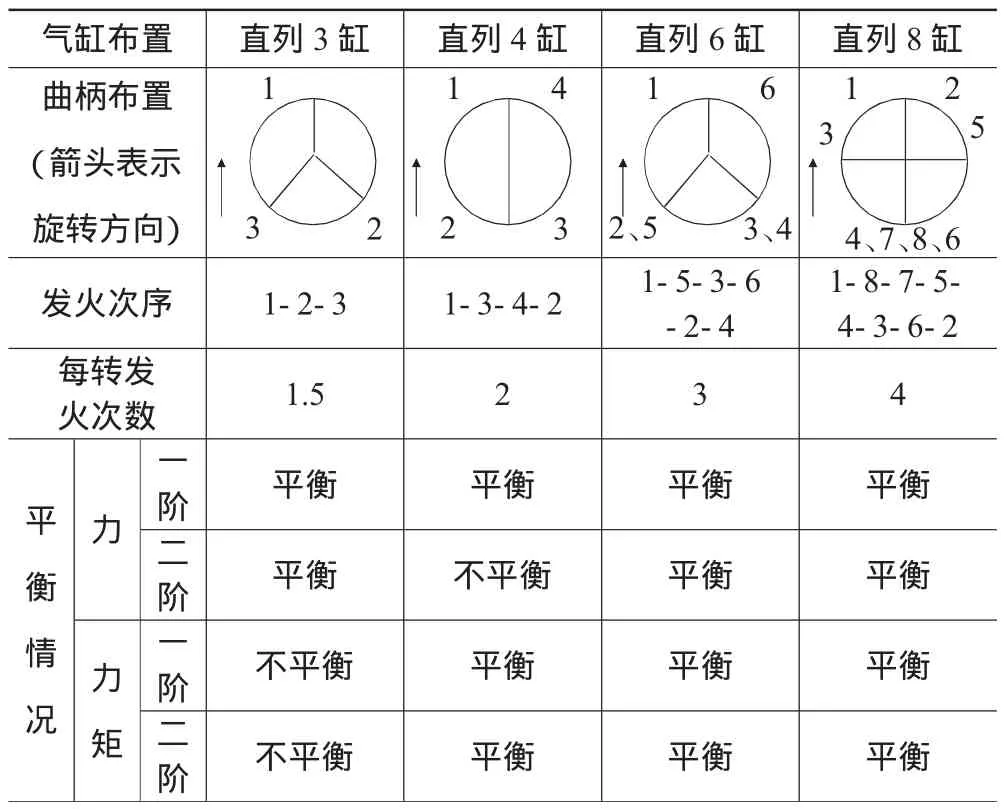
表1 四冲程往复式内燃机固有平衡特性表

对于发动机悬置系统参数进行优化，可以从不同角度提出目标函数和约束条件来建立不同的数学模型。常见的目标函数有：发动机悬置系统六自由度解耦和部分解耦；系统固有频率的合理配置；系统的振动力传递率或支承处动反力最小[3-5]。

根据振动理论，悬置系统的隔振设计主要从系统的固有频率考虑，当系统的固有频率和相应的扰动频率相同时，振动系统将发生共振，相应幅值大大增加。对发动机而言，低频范围内，其主要扰动力为绕曲轴方向的转矩。当此扰动频率和绕曲轴旋转方向RY的固有频率重合时，系统发生共振。通常使RY方向的固有频率小于发动机正常工作时扰动频率的0.707倍。同时，从整车各子系统的动力特性合理分配考虑，悬置系统的固有频率还应避开其它子系统相应的振动频率，如悬架、车身及车轮的振动频率，以防由此引起发动机和其它子系统间的共振。此外，还要使悬置系统主要方向的振动得到解耦，至少也应该使它们的耦合程度得到降低。所以，无论从发动机悬置系统，还是汽车其它子系统的动力特性合理分配考虑，对发动机悬置系统的设计都必须从解耦和固有频率的合理设计入手[6-9]。

1.2 建立目标函数

根据发动机悬置系统优化设计的要求，将固有频率、解耦性用数学模型表示。通常对Z方向及RY方向的固有频率和解耦性有较高要求，而其它振型的固有频率只要控制在一定的范围内即可，于是建立如下目标函数：

式中：x为设计变量；f0（z）、f0（RY）为设计要求的固有频率值；f（z）、f（RY）为悬置系统的实际频率值；dig为解耦性（100%，完全解耦）；W1、W2、W3、W4为加权系数。

1.3 能量解耦法

对动力总成悬置进行优化，常采用能量法进行解耦设计。能量分布矩阵是动力总成在做各阶主振动时的能量分布，写成矩阵形式，记作KE[10-11]。当动力总成以第k阶固有频率振动时，第i个广义坐标分配到的能量（KEi）k为

式中：mij为动力总成质量矩阵中位于第i行、第j列的元素；（φk）i、（φk）j为第 k 阶振型中第 i、j个元素；ωk为第k 阶振动的固有频率(i，j，k=1，2，……，6)。由此可得,以第k阶固有频率振动时，第i个广义坐标所分配到的能量在总能量中的百分比：

式中：（KE）k为悬置系统的总能量；digik表示悬置系统在i方向的解耦程度，digik越大，解耦程度越高。

2 参数及设计变量优化

该车型采用横置直列三缸汽油发动机，三点橡胶悬置，其中后悬置为抗扭拉杆式，系统布置如图1所示；动力总成转动惯量和惯性积见表2；悬置的位置和刚度参数见表3。

表2 动力总成参数

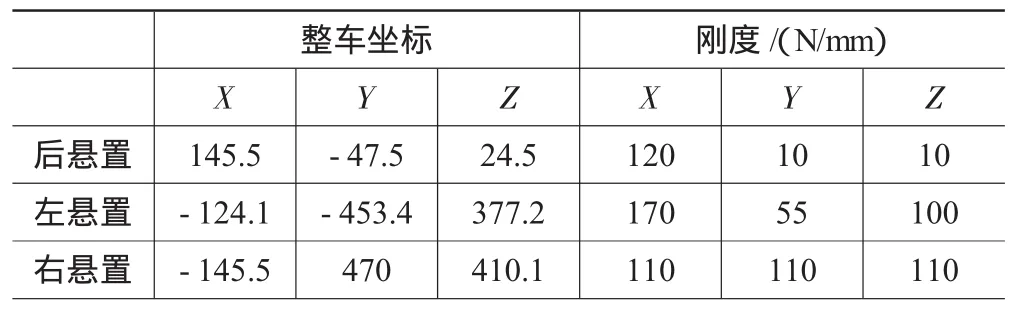
表3 优化前位置及刚度

由振动理论可知，刚度矩阵与以下因素有关：动力总成悬置的个数、各悬置的安装位置、各悬置的弹性主轴与广义坐标系之间的角度、各悬置在弹性主轴方向的刚度。其中调整悬置的位置对刚度矩阵及系统的解耦率影响最大，收效也最明显，但考虑到该车型发动机舱及底盘的方案均已冻结，调整悬置位置将引起较大的设计变更，成本太高，故决定选择悬置刚度为设计变量。

由前面分析可知，当动力总成绕曲轴的固有频率小于发动机怠速激励频率的0.707倍时，才能达到隔振效果。本例中三缸发动机的怠速转速为850 r/min，由式（4）得发动机的激励频率为21.25 Hz。因此，绕曲轴方向（RY）的固有频率必须小于15 Hz。

式中：n为发动机转速；i为发动机缸数；τ为发动机冲程。

由式（2）、式（3）可得优化前动力总成系统各阶模态和能量分布情况，见表4。可见，X方向和RY方向固有频率过于接近，且绕Z轴旋转的固有频率RZ=21.7与发动机怠速的激振频率也过于接近，振动存在耦合，六自由度解耦程度不够，是导致整车振动的主要原因。

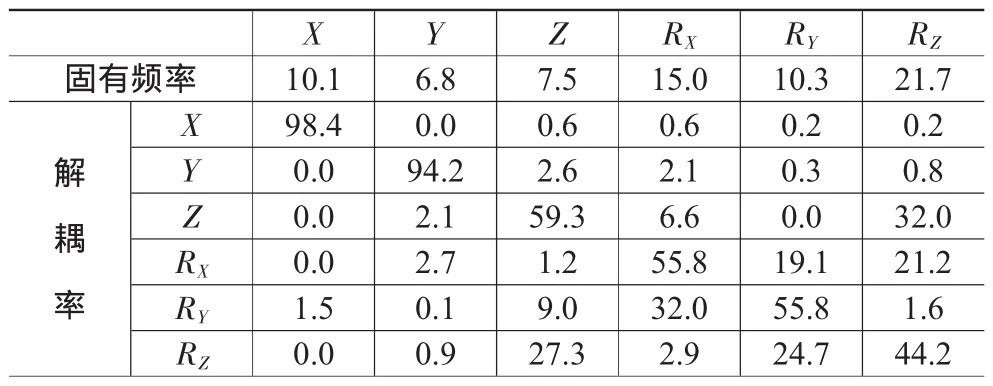
表4 优化前能量分布

结合原悬置系统悬置参数进行优化计算，计算中取加权系数：W1=3，W2=3，W3=2，W4=2。优化计算后悬置刚度及动力总成悬置系统的固有特性见表5、表6。从表5看出，优化后的右悬置的刚度比之前变化不大，左悬置的X方向刚度值降低较大。表6表明，动力总成悬置系统RZ方向的固有频率由原来的21.7变为18.2，与激振频率错开；X方向和RY方向的固有频率也间隔了1 Hz；各方向解耦率都在80%以上，满足解耦要求。

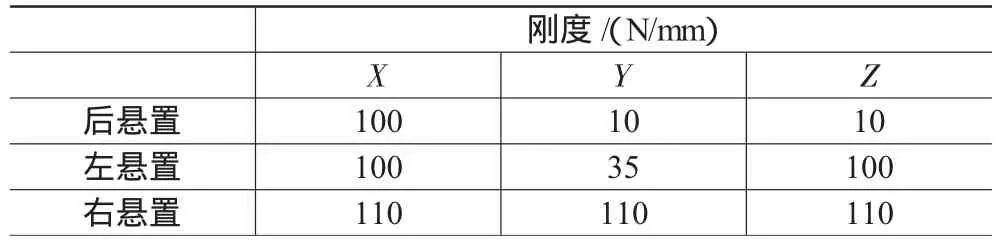
表5 优化后刚度

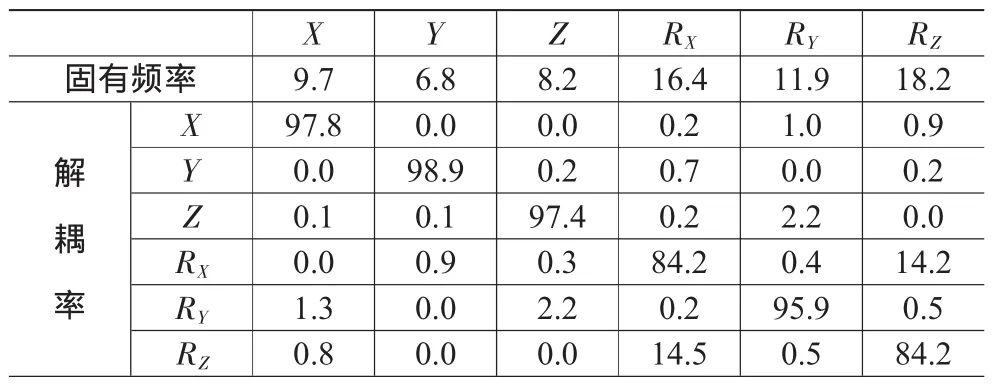
表6 优化后能量分布

为了验证悬置优化后的隔振效果，对原车悬置系统优化前后进行了整车振动试验。通过试验得到，各测试点的振动传递率柱状对比图、车厢地板及方向盘的振动加速度有效均方根（RMS）值如图2、图3所示。从车厢地板振动能量的测试数据来看，悬置优化后，整车怠速的振动状况得到了较好的改善，振动加速度RMS值在汽车低速及中速行驶时，均低于改进前。

3 结束语

发动机悬置系统设计是一个比较复杂的问题，涉及的因素较多，其设计的优劣对整车的振动特性会产生重要的影响。理想的发动机悬置应能隔离发动机在转速范围内引起的扰动，并能防止路面激励引起的振动。本文对该车悬置系统刚度参数进行了优化计算及改进设计，并通过整车振动试验证实了理论计算的正确性，用最少的变动、最低的成本使该匹配三缸发动机的车型的振动情况得到了改善。

[1]庞剑，谌刚，何华.汽车噪声与振动—理论与应用[M].北京：北京理工大学出版社，2006.

[2]周龙保.内燃机学[M].北京:机械工业出版社，1999.

[3]吕振华，范让林.动力总成－悬置系统振动解耦设计方法[J].机械工程学报，2005，41（4）

[4]黄信，柏世川，章竹一.汽车发动机悬置系统设计[J].合肥工业大学学报：自然科学版，2009，（S1）

[5]徐石安.汽车发动机弹性支承隔振的解耦方法[J].汽车工程，1995，（4）：198-204.

[6]侯勇，赵涛.动力总成悬置系统解耦设计[J].汽车工程，2007，12.

[7]周志革，武一民，崔根群，等.发动机悬置系统参数的优化设计[J].机械设计，2003，20（3）：53-55.

[8]范让林，吕振华.刚体－弹性支承系统振动解耦评价方法分析[J].工程力学，2006，23（7）

[9]Seonho Cho.Configuration and Sizing Design Optimization of Power train Mounting Systems[J].Intenrational Jounral of Vehicle Design，2000，24（1）

[10]王天利，孙营，田永义.基于能量法解耦的汽车动力总成悬置系统优化[J].机械设计与制造，2006，（7）：31-33.

[11]周密，侯之超.基于遗传算法的动力总成悬置系统优化设计[J].汽车技术，2006，（9）：13-16.