面向气候变化的复杂地球系统建模与模拟探索（下）＊

查传捷 李 琦②

①研究员，②教授，北京大学数字地球工作室，北京100871＊ 创新方法基础性设计与实施（2008IM05100）

面向气候变化的复杂地球系统建模与模拟探索（下）＊

查传捷①李 琦②

①研究员，②教授，北京大学数字地球工作室，北京100871
＊ 创新方法基础性设计与实施（2008IM05100）

公设化 混沌 非线性 非连续性 蝴蝶效应 吸子

科学界有一种不成文的法则：物理是具体模式，其原始术语摘自于真实世界的对象与关系。数学则是理想模式，其原始术语来自于对猜想的演绎。一般说来，物理学以观察、测量与实验为现象辩护。数学则是以推理演绎为物本身辩护。前者是对物理现象的诠释，后者是阐述事物隐含的本质。显而易见，这两种知识有本质上的差异，亦各有先天的盲点与缺陷。因此在入门的瞬间，彼此不一致的裂痕业已出现，并延续下来。这就是千百年来科学知识疑窦丛生的肇因。这篇论文秉持真理，根据宇宙时空结构转换所遵循的自然律为立足点，更为数学打开了通往物理公设化（axiomatisation）的门扉，进而令数学与物理学一致，以破解千百年来科学界“悬而未解”的种种问题，从根本上彻底消弭了自古以来令数学与物理陷于严重困扰的基础危机。

人类在有文字之前已懂得结绳记数，但对于数字的本质，迄今仍未能完全清楚。所以庞加莱在1897年苏黎世举办的第一届国际数学年会上演讲时指出：数学的目标是为了了解时空结构与自然律、数字的概念，以及美学［1］。

1 数字的概念及无理数问题

据数学史料记载，早在公元前5世纪以前一位毕达哥拉斯学派（Pythagorean）的成员伊帕索斯（Hippasus）因为发现 “”而大肆吹嘘，结果被丢进大海。这篇论文既非对数学史的补遗，也不对史料考据感兴趣，而是为了阐释数字概念及其与宇宙构成的元素（原子）两者之间的关系。所以，先从数学界宣称业已破解的希伯特第四个问题着手，这个问题亦即源自于“2 ＝”的证明。由于数学界无法提供答案，因此被界定为题目过于含糊而舍弃掉了，后来变更为直线与最短距离问题，并衍生出一门数学的旁支——“变分法”，藉由在极值附近点的特质，找出一种恰当的函数曲线，来解释几何证明极限时所产生的问题。其实这个问题，也就是对无理数极值的探索。况且古希腊的自然哲学原本就没有数学与物理的区分，若以此为出发点整合数学与物理，不亦宜乎？

考虑等腰直角三角形△AOB，令线段AO和OB长度皆为1，因此三角形△AOB斜边的长度为“”。当然，数学家们可以轻易地指出：一个单位等腰直角三角形直 角 对 边 的 长 度 是 “”， 但 锯 齿 线AO3A1O4B1O5A2B2B长度为2。（每段长度皆为1／4。）如此继续下去，岂不是可以几何证明 2 ＝？这就是无理数极值的问题，如图1。

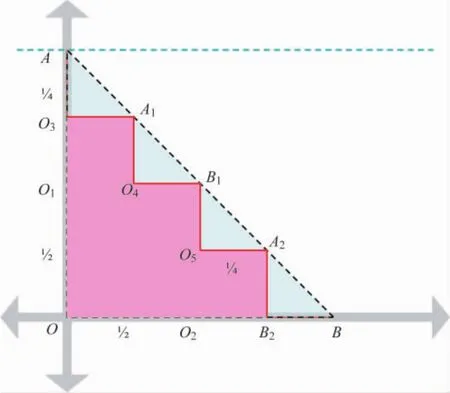
图1 以几何证明 2 ＝

数学的目的是探究真理，数学是解释自然的工具，而不是随心所欲制造一些莫名其妙的东西。凡是基于不存在幻想的论证是无效的。伊帕索斯的“”并不是一件前所未有的“发现”，而是“创作”了一件子虚乌有的东西，徒增后世学习者的负担，因此被丢进大海也算是咎由自取。正确的逻辑演绎，并不等于正确的答案，若没有正确的前提，正确的逻辑也不能演绎出正确的答案，这叫做：“垃圾进来，垃圾出去（garbage in and garbage out）。”希伯特认为这个问题或许可透过测地线（geodesics）诠释［2］，如图2。

图2 测地线示意图

一般测量得到的数据，往往依尺码长度而定。显然一尺一尺的度量远比一哩一哩的度量要长。一般测量的误差往往超过40%，或许也算是“证明”了测地线一步步地趋近于1.414 213 562…但始终无法成为真正的”，却又恰好超过40%！然而不论测量的技术如何进步，都没有办法测量出河流、国界与海岸线真正的长度。当测量的尺度小到尽头，无可避免最后都变成了一团没有部分的原子。可是原子的模样至今仍是科学未解之谜。况且还有一个海森伯的测不准定理在一旁虎视眈眈。

若不斤斤计较确切长度的极值，那么古埃及的拉绳者们只要一根棍子及一条绳子，就能够轻易地量出一个单位正方形对边的长度大致是1.414…奈何“”是个斤斤计较的东西，只要改变其中任意1个数字，它就再也不是”了。事实上迄今也未有人能够真正写出一个正确的”。请看下面的方程式，图3的Heighway’s Dragon［3］似乎为这个极值问题揭开了神秘面纱的一角：

就物理模式而言，它无法成为观察、测量与实验的对象，也无法落地。即使拿宇宙中所有的原子来充当数字，也无法写出一个”。严格说来，无理数根本不算是数字，而是一个字母、一个符号；因为它虽说阐述事物隐含的本质，却非依据事实。所以无理数只是一个理想的模式，并不存在，这也就是数学的第一个基础危机。

17 世纪早期就有了以字母与符号取代繁琐计算公式与冗长数字的表达方式。这种简洁的表达方式影响十分深远，逐渐改变了数学的本质，又蔓延到其他的科学领域。

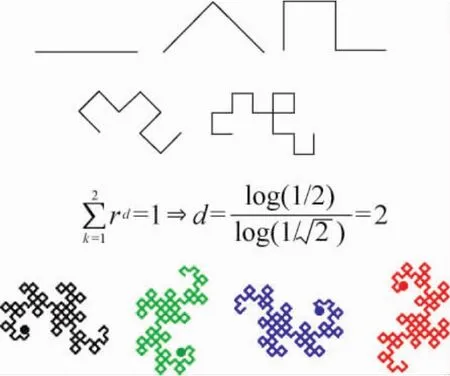
图3 Heighway’s Dragon

希伯特更是全心全意相信符号，他甚至还在《约翰福音》中加上“太初有符号”，他将其解释为无意义的符号，可以任意重复。反之，有意义的符号，如2就是1＋1的缩写，于是1就是1／2＋1／2，也是1／4＋1／4＋1／4＋1／4，或1／4＋3／4，或1／8＋7／8，或3／8＋5／8，…；又譬如字母“a，b，c，…”代表任意数；“x，y，z，…”代表任意未知数；“f，g，h，…”是函数，诸如此类的表达方式，尤其在全新的领域由于没有现成的表达方式，就出现了大量的符号，配合着崭新专有名词与方程式。然而名词定义往往暧昧不明，方程式的描述方式也有待商榷。

这里举个简单的例子：计算一个鸡蛋的体积。

当然你可以应用微积分及公式花费几小时，或几分钟求出一个近似值，误差不超过±10%。或许，你也可以学阿基米德将蛋丢进装了水的量杯中，只要花费几秒钟，就可以求出一个近似值，误差大概不会超过1%。

这种奇怪的计算法当然经得起重复验证，或许物理学家也会欣然接受？或许还有一些研究基因的学者们会更进一步睿智地宣称：因此证明，“鸡”只不过是“蛋”用来复制自己的工具罢了。

2 方程式与代数“解”

探讨方程式的解法，至少应该回溯到16世纪初。这一段数学史上最辉煌灿烂的成就，是意大利数学家们在三次与四次方程式的代数“解法”上投入的努力。

三次方程式求解可回溯到德利安问题或倍立方问题。倍立方问题，就是求，相当于解三组抛物线与双曲线方程式：x2＝ay，x2＝bx，xy＝ab，也就是：a∶x＝x∶y＝y∶b，又称黄金分割、求中项比或斐波那契数列，显示出一个源远流长的问题，即无理数的存在性问题。

早期有关方程式的代数“解法”是从数学的“擂台赛”拉开序幕。在这里可能有必要再一次复习一遍三次方程式的通式：

当时数学家们并不知道这种表示法，他们将此通式分门别类，分成为13种不同的类型，然后分别处理，寻求解法［4］。

三次方程式的“解”究竟是什么模样？

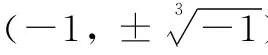
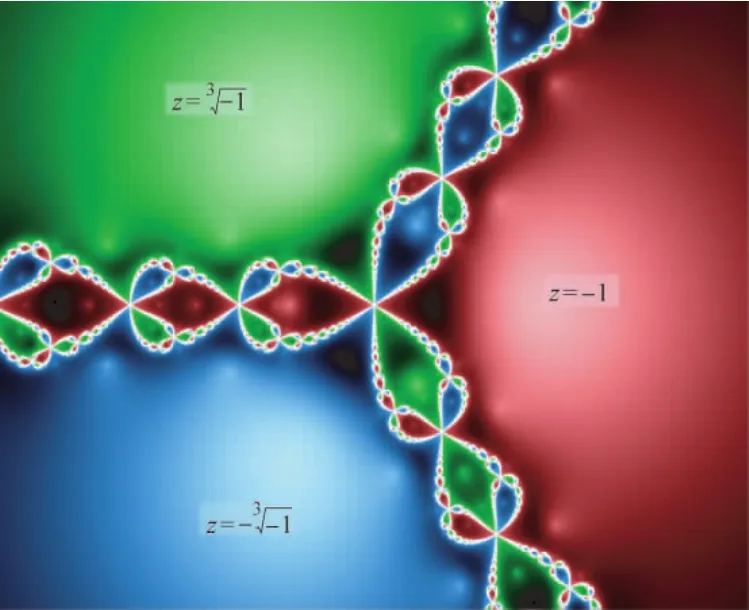
图4 电脑绘制的非线性三次方程式f∶z→z3－1的解

转眼三次方程式的热潮已过，紧接着“五”次方程式登上舞台。五次方程式的问题更加复杂，不过此时方程式“解法”的方向，也已经悄悄地朝向“无解”的方向进行。

意大利物理学家鲁菲尼（Ruffinii）［5］首先提出五次方程式“无”代数解，他发表了两册篇幅长达516页的巨著，不过推理过程曲折，十分难懂，数学界毫无反应。而后鲁菲尼又再接再厉，以更严谨而且更为浅显的推理过程，分别于1803年、1805年、1813年又提出了3次［6］，不过始终引不起当代数学家们的注意。最后鲁菲尼在意大利走投无路，只好将他的证明寄给英国伦敦皇家学会。随后他收到了一封措词十分婉转的回函：尽管有几位会员读了他的作品还算满意，不过基于学会的政策，不能对任何证明背书。此后五次及五次以上方程式的解法，逐渐悄悄地由有解转向无解。而后由挪威的天才数学家阿贝尔（Niels HenriK Abel）担纲，接演五次方程式“无”代数解悲剧的续集。在阿贝尔早年的论文中，他证明了五次方程式不可能有代数解。这是由于他发现了超越数的缘故。阿贝尔这篇号称是当代数学界最伟大的论文，当时根本没有人读。不过他并未在论文中提出超越数附近极值的特性。

阿贝尔13年后在《纯数与应用数学年鉴》（Journal fürdierieneundangewandteMathematik，1826，known as Crelle’s Journal）的创刊号上留下了5篇论文［7］，其中就包含了对超越函数、无穷级数的收敛性与椭圆函数等重要数学概念的探讨。在次年的年鉴中，他的双周期函数理论紧接着诞生。

同时，数学界另一位悲剧天才伽罗瓦（Qvariste Galois）也提供了另类的诠释。伽罗瓦的论文导致群论的诞生，为科学家打开了一扇通往真理的门扉，不过仍未能将数学与物理调和起来，当然也不能提出具体的物理答案。

超越数最著名的例子，就是圆周率π。

古希腊著名的几何问题化圆为方（quardrature of the circle），也就是求圆周率。对此当年希腊有一个专门术语：τετραγωνιξειν，意思是一生献身于“化圆为方”的人。其中的佼佼者名叫安迪丰（Antiphon，Αυτιφωυ）。据数学史书中记载，他提出了“穷竭法”来寻找答案。其实穷竭法，也就是说永远无法找出答案。

从来没有任何一个其他数字，能让数学家们投入如此多的心血。

据悉有人用20世纪的超级计算机，夜以继日地计算。最后终于计算出了510亿个小数点的近似值，这可真是需要大书特书哪！因为这个数字若以平常的方式印出来，长度可达61 200英里（98 492 km），差不多可绕地球两圈半，只可惜仍旧是近似值［8］。这也无可厚非，因为计算圆周率的电脑程式，被电脑界称为：无限循环的臭虫（bug）。后来干脆拿来当作评鉴电脑速度与可靠性的“标准”，也算是因势制宜，物尽其用。

事实上，无论是21世纪的超级计算机，还是英国数学家艾伦·图灵（Allan Turing）的图灵机，甚至电视科幻影集StarTrekWolfintheFold中的“邪恶电脑”，也描述不出任何一个无理数，遑论超越数？

近年来更有人利用电脑绘图，绘制出曼德布洛特集合（Mandelbrot set）、柯赫曲线（Koch-curve）、劳伦斯吸子（Lorenz attractor）等等图案，更进一步诠释出极值在附近点的特质：五彩缤纷的图案看来无序，显示出它们根本无法收敛，却环环相扣！

随后又出现分形、混沌的理论相互呼应，猝然进入了混沌与模糊数学的领域。

其实根本用不着依赖任何现代科技，古埃及的拉绳者们只要一根棍子及一条绳子，就能够求出圆周大约为直径的3倍，如果有一把精确的尺，更可以求出圆周率的值约为3.141 592…

奈何圆周率又是一个斤斤计较的东西，容不下一丝一毫的差池，只要改变其中任意1个数字，譬如：只要将第五位数由5改为6，它就再也不是圆周率了［9］。

大自然时空结构无限折迭（fold catastrophe）、迭代（iteration）让尺度的大小失去了意义。

再举一个例子来说明专家们对极值的谬误观念，请看下面这一条取自古希腊欧几里德的几何问题［10］：无限交错数列S＝1－1＋1－1＋1－1…

S＝a（rn－1）／（r－1），其中r为比值，a为首项值。

S的极值是什么？

有一部分人认为：

S＝（1－1）＋（1－1）＋（1－1）＋（1－1）… 所以极值为0。

另外一部分人认为：

S＝1－（1－1）＋（1－1）＋（1－1）＋（1－1）… ＝1－S，所以极值为1。

现代的数学家们，则采取欧拉（Leonhard Euler）提出的解法：

因为S＝1－S，所以2S＝1⇒S＝1／2。

这里有50%的机会可以找到0，也有50%的机会可以找到1，但绝对找不到1／2！因为1／2在数列中根本不存在！所以这只是概率的答案，而非极值的特质。欧拉善于舞文弄墨又喜欢卖弄聪明，这就是欧拉自谓“改不掉的老毛病”，也是模糊数学问题之所在。

3 罗素悖论及模糊数学

模糊数学是美国控制论专家扎德（L.A.Zadeh）为研究实际问题，以集合论为基础，将随机性、概率、统计为数学工具，而衍生出来的一门边缘学科［11］，成为类比系统理论的根基。类比电脑的运算速度无可非议，但是随机性无法控制亦无法仿真，所以业已被数字电脑所取代。

集合是以德国数学家策梅罗（Eerst Zermelo）的策梅罗公设（二值逻辑）为基础，但出现了罗素悖论（Russell’s paradox）：一个不包含自己的集合。

扎德企图要将随机性、概率、统计学引入集合论，辄以非亚里士多德逻辑取代策梅罗的二值逻辑，于是对元素x与集合S给出了一个特征函数C（x）：

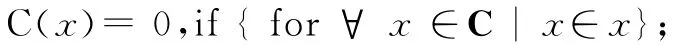
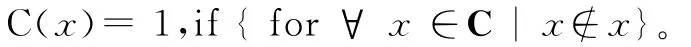
在给出此一特征函数C（x）定义时，扎德舍弃了集合论中严谨的集合（Set）观念代以较为模糊的“级”（Class），用较松散的局部属于关系（∈－partial-order relationship，i.e.，min（a，b）and max（a，b））取代联集与交集（union，∪，intersection，∩），并以封闭性区间［0≤x≤1］，取代二元集合｛0，1｝。

换言之，扎德给出的特征函数C（z）＝｛for∀z∈C｜f∶z→z4＋1，where［0≤｜z｜≤1］，and Cis complex number｝中，C（x）＝0是集合，C（x）＝1不是集合。若给出了一个封闭性区间［0≤｜z｜≤1］，事实上亦代表极值0存在。若以方程式f∶z→z4＋1界定特征函数C（z），就是将函数域（range，i.e.，image domain）由二元集合｛0，1｝扩张至无限的复数领域中［12］，如图5。

方程式的四个根（±1，±i）将平面分隔成四块区域，每一个解中隐含着其他三个解，形成一片蒙蒙复谲的杂诡边界，看不见最终的结构。这就是方程式极值在附近点的特质。无限永远也无法收敛，若可以收敛，那它就没有无限的特质了。若更进一步仔细分析，就知道这是古希腊著名的“化圆为方”几何问题，也就是将圆摊平在高斯的复数平面（C＊，the set of complex number without addition zero）上。

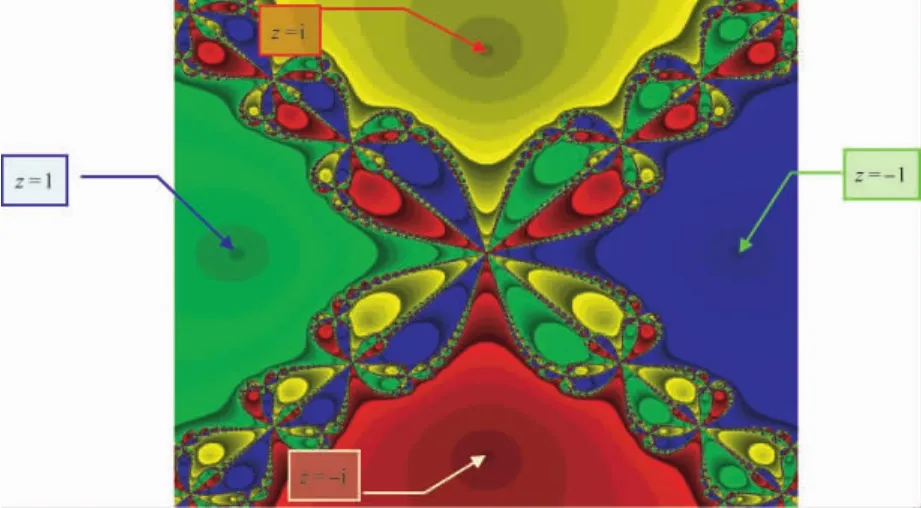
图5 在复平面以牛顿法（Newton method）解方程式：f∶z→z4＋1

众所皆知，概率是比值，统计也只能处理可数的事物，有理数乘法不封闭，没有乘法反元素，乘法交换律不成立，所以在模糊数学中互补律（A∪A′＝E，A∩A′＝Ø）不成立。尤其模糊数学中的数字应该是离散与量子的，界定级的陈述也不能使用微积分或是非线性方程式。因为非线性方程式无法相加，况且无解。

由于在模糊数学使用局部属于的关系，所以一般的真值表并不适用；在一般数学中的结合律（a☆（b☆c）＝ （a☆b）☆c）、交换律（a☆b＝b☆a）、分配律（a★（b☆c）＝ （a☆b）★（a☆c））…也需要检讨［13］。

事实上，多值逻辑与双值逻辑本是同一件事，只是增加一个Do-loop，也就是电脑硬体中的回递线路，所以无所谓非亚里士多德逻辑，见图6。

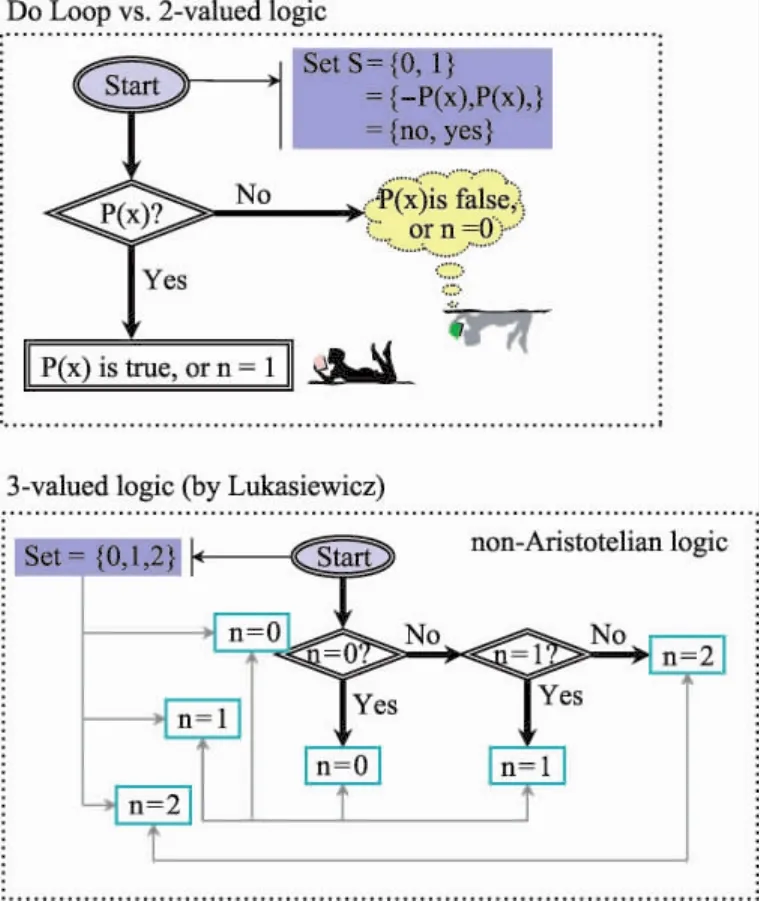
图6 多值逻辑与双值逻辑

4 极值的收敛与无限的代数性

科学家们显然曲解了极值与无限的代数性，以为只要是函数收敛就有极限，就可以找到极值解决问题。

这真是大错特错！非线性方程式的极值根本不会收敛，也不能使用微积分表述！

若从物理角度看，函数是阐述物理与化学反应的方程式，每一次越过临界点，就产生分子结构重组。例如：解诺维尔·史托迈尔这类方程式，就好像走迷宫，每走出一步之后，迷宫的墙壁就会重组，这是非线性斯托克斯流体动力方程式（Navier-Stokes equations）面临的问题。正如冯诺曼（John Von Neumann，1903—1957）所言：这种方程式的特性是同时改变所有相关的特性，包括次序与维度一起改变，因此高难度的数学是可预期的。

很少有人能够跟得上目前科学专业发展的步调，各行专业类别间，就像是战舰上防水闸门般密封阻隔着，专家们自顾不暇，毫无余裕来阅读其他类别的期刊。没有人会在气象的期刊中寻找混沌的理论，也没有几个人会在应用科学的期刊中寻找模糊数学的理论。

在混沌的理论里，数学家们仿佛遇见了双面神杰纳斯（Janus），从这一面看去看到了秩序中掺杂着随机性，从另一面看去，则看到了混沌的复杂系统中隐含着与生俱来的秩序。然而对任何一位科学家而言，掌握几条数学公式，要比描述庞大的自然细节要简明多了。因此科学家们寻找答案的目标，已不仅仅只是为了正确地描述宇宙，并且还要以最简明扼要有效的方式描述出来，这就是奥坎剃刀（Ockham’s Razor）原则——以最少的方式，巨细靡遗描述出大自然所有的细节。

迭代、折迭与逻辑“自洽”的本质导向分形结构与混沌理论。分子结构自发性失称与自我复制的规则，隐藏在脱氧核糖核酸（DNA）中，复制出缤纷的大千世界。

这亦是大自然演化出生命游戏所采取的时空转换规则。

倘若极值是无理数，这可是图灵机也无法解决的无限问题。不论诺曼的图灵机还是诺维尔·史托迈尔方程式，都逃不出无理数的纠缠。交错级数看起来诡异，其实也只不过是另一种描述无限的方式：循环，它在物理的宇宙中，即所谓平衡。当条件到达临界点时，就产生相变。相变皆源自于分子结构的崩解，当物理、化学与生化反应同时交换一小包能量，若能量突破阈值，就导致结构的崩解，系统突变。

当科学家们计算公式取近似值时，他们也同时在主张，这些微分方程式的解答是由无限项次所构成，他们所凭借的是假设其余的项次影响不大，所以只要计算其中的前几项就能取得合理的近似值。但一小段直线上的点与无限长的直线、无限大的平面，甚至整个空间中的点数目是一样多，这一点可以用导体中电荷的屏蔽效应证明，也可以用数学的高斯定律证明［14］。

牛顿首创摄动原理，然后企图以流数法来解答三体运动混沌的轨迹，却始终未尝成功。牛顿无法解开太阳、月球与地球间的三体运动问题，因为行星的轨迹既混沌又不连续。只好拼凑出近似值，设法让计算式中的数据吻合测量的数据，这种方式虽嫌粗糙，但原则上也还说得过去。因为当年牛顿与莱布尼茨所描述的轨迹与其说是连续的，不如说是稠密的；牛顿本人从未提到过连续性，也没有无理数。

只怪后来的数学家们为了让微积分合理化，加上了连续性与无理数，又创造出导函数，并为它建立了连续统假说。

数学的角色应该是使科学的理论发光，而不是用臆想的术语来让人莫测高深；也就是必须用事实来为数学划出是非、分界，而不是被无限的演绎牵着鼻子走。若不能清楚是非、分界，那岂不是治丝益棼？又怎能清楚合理地去描述这个充满了混沌的领域呢？

事实上，不论科学家们如何竭心尽智，他们应用的微积分或流数法又如何高阶，使他们误以为答案已趋于极值；一旦删去“尾数”，就等于删去了“无限多”的点，也就是将无理数变成了有理数。

5 建立离散数字

一旦摘除了原本的连续性，就改变了数字的代数性。更糟的是，这些改变蔓延到所有的物理量，进而延伸至科学所有的领域。就这样，正确的答案一再从科学家们所设下的精妙公式与数字的陷阱中溜走。

数字一定是连续性的吗？量子力学不是连续性的！

无理数存在吗？电脑中没有无理数！

为了避免正确的答案从公式与数字的陷阱中溜走，最明智的方法是摘下连续性与无理数的枷锁，建立离散数字。

首先，取自然数“n”的倒数1／n。1／n相当于自然数“n”的加法与乘法反元素。因此可以定义一个一对一映射函数（Φ）：将所有的自然数对应到一个半开放的单位区间（0，1］，区间中元素的数目与自然数（N）、正有理数（Q＋）相等（也就是，∞）。

由于无限大“∞”不存在，它的倒数“1／∞”也不存在。所以这里出现一个不含“0”的半开放区间（0，1］。若再以这个半开放区间（0，1］做单位尺标可以建立一组稠密的数列：①，②，③，…数列中每一单位中的点数与自然数相等（也就是，∞）。所以数列的大小与实数、复数的大小相当（也就是，2∞）。若依样画葫芦，再令○n⇔1／○n，可以得到另一组更稠密的超越数列：❶，❷，❸，…整个数列的大小为（2∞）∞，相当于数学中所有的函数转换，也相当于宇宙中所有物理的质能转换。

这就是目前为止，科学家们在自然界中找到的所有无限大，显然也只有这三种无限大属于物理的世界，所以它们也通过了存在性的检验。以此类推，也可形成任何大小的不连续数列。（也就是，（（…（（（2∞）∞）∞）∞…）∞）∞），不过这些无限大在自然界中找不到，因此最好还是适可而止，避免违背了“存在性”。

这种数系的代数性与一般的数字大相径庭，具有各式各样的“反元素”，离散而封闭。封闭性是数字具体化过程中不可或缺的必要条件之一，也是数字“二元运算”的必要条件，更阐释出宇宙中没有任何可以超越二元运算的具体东西，因此解决了多次元问题，排除了量子力学中不可思议的多重宇宙理论，更明白指出宇宙中的无限只有可数的无限及不可数的无限两种。

目前所有数学中所熟悉的集合，无论有限、无限皆尽于此。譬如：N，Z，或Q，属于可数无限集合；R与C则属不可数的无限集合。

显而易见，整数（Z）不连续。自然数这个集合虽说无限，但不封闭，也没有反元素。所以它无法逆运算，既没有减法也没有除法，也就是说，算不上是“二元运算”。同样，正有理数（Q＋）也有同样的问题［15］。

在物理世界中虽找不到 “＜1”的东西。不过却找得到对应于 “＜1”的反元素，譬如电子的反元素质子，也有影子与镜像，皆是具体的物理现象，也遵守大自然的物理法则，甚至可以确实执行。因此，虽说 “＜1”与负数不存在，然而对应于 “＜1”与负的现象却“存在”。不过无理数与超越数不存在，它们只是子虚乌有的理想与符号。

不过这种数字并不均匀，在那些半开放区间（0，1］附近特别稠密，有如元素原子的光谱一般，所以没有存在性的问题。至于这个半开放区间（0，1］，就是一般所谓的丛点；或者更时髦的说法，就是混沌的奇异点。

接下来再解决“0”的“存在性”问题，“0”就用来阐释宇宙中的虚空。若时间差为“0”，距离与位置也就失去了测量的基准，因而形成了时空的奇异点。这就是芝诺的飞驰之箭在物理空间所划下的轨迹，也是测不准定理的缘由。

因此可以透过原子光谱的精致结构发现“原子”附近的时空特别稠密且不连续，而原子的塞曼-斯塔克效应（Zeeman-Stark effect）也可以证明。况且虚空本来就什么也没有，也就是空集合（Ø，或｛｝，这是一阶的 “0”：），一个由等值时间面构成的拓扑性封闭“空泡”，这是二阶的 “0”。既具有caridinal set的特质，又具有ordinal set的特质。至于二阶以上的“0”在自然界中找不到，因此还是暂时割爱，避免违背了“存在性”。

Definition：The zero of Billy’s number：B1and Billy’s knots：B2.

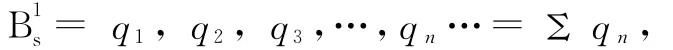
An empty isochronal topological closure sphere：，is the second level“zero”，an initial element for Billy’s knots，the set：，which generate from a single light source S，is a “partially order class”in 3-D space，where，andis the unity element in B2，where“i”is subscripts.

真正的连续性与封闭性只存在于二阶结构——原子的球面。这也就是为何一阶逻辑可以阐述原子与宇宙中基本元素的一阶特性：因为它们是离散的，并不连续。至于二阶逻辑，则用以阐述原子与宇宙的二阶特性：具备各式各样的反元素，也就是这些反元素足以让它们封闭。就是这缘故，它们存在；也就是这缘故，它们可以具体化。

假设B2s为光源S的一个时空节点，而等时拓扑封闭小泡内含的能量为｛q｝，则q就是小泡内含的一小包能量。

如此一来，能量与质量的关系与集合论元素与集合的关系不谋而合。至于将能量束缚在时空节点B1中，科学家将它称为弱核力（week nuclear force）。所以光量子（light quantum）是集合中的单一元素（singleton），定义为：｛q｝∈，也是光源S的successor set S＋。因此时间包含在时间内（time∈time），也清楚指出时间不包含在时间内（time∉time）；所以也消弭了罗素悖论（Russell’s paradox）的疑点。

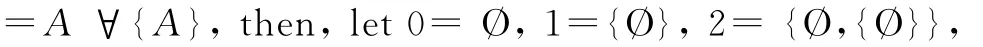
这种方法称为construction by recursion，或视为是Axiom of Infinity等价。于是A＋B＝A∪B，A－B＝A∩B′，这就是一般数学的加法与减法。

只不过非线性系统无法相加，亦往往无解（也就是混沌），在流体与机械动力系统中往往是被舍弃的部分。以摩擦力为例，若没有摩擦力，只要一条惯性方程式就可以搞定；但加入摩擦力后，系统立即变得复杂无解：找不到极值。在大自然的游戏中非线性主宰游戏的“数字与运算”规则，线性只不过是特例。事实上，数学的“数字与运算”物理化时所面临的问题，是在无限中寻找极值（穷竭法），及非线性系统中的反元素或“反运算”问题。除法就是反乘法或乘法反元素的乘法，它的数学定义如下：

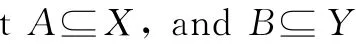
其实宇宙中任何物体都是集合，所以任何大自然的“数字与运算”皆来自于集合“属于”（∈-well-order relationship）的关系，这正是集合唯一的关系。根据“construction by recursion”或“Axiom of Infinity”，只要借着空集合（Ø）与successor set即可应用“属于”的关系建立所有的“数字”与“运算”（注：属于等价于集合的联集（∪）与交集（∩））。

因此也只要先具体化空集合与successor set，同样可以应用属于的关系具体化所有的“数字”与“运算”。然而任何一个集合A的二元运算，亦即集合的转换，可视为是集合对自身的排列组合ρ，并不关切集合内的元素是否无限，只要记住，运算的步骤必须是可数的无限。而任一ρ，相当于一对独立、不接圆（或许更恰当的描述是不接环）的排列组合。因此，可以用它们的旋转代替乘法运算（⊗）。换言之，任一次不接环的旋转皆相当于两个加法交换群的乘积，而每一个“群”都必定与某组排列组合同构，旋转只形成“循环群”。有限交换群也就是循环群。所以，任一转换函数ρ，皆相当于将若干不接圆迭加起来，一并做有限次数的排列组合，运算也就是共集合有限次数的指定运算，只限定运算次数有限，不接圆与元素的数目根本没有任何影响。如此一来，就解决了无限的问题。

若令（0，1）∪｛1｝＝（0，1］，无疑也可以一对一对应于一个直径为1的单位圆。此外，也可以很容易证明，单位圆、任意圆、矩形，或几何图形中的点也一样多。以此类推，可以证明任意二维拓扑结构，甚至整个三维空间中的点也一样多。

换言之，任何一条直线可以无限“迭加”与“分割”，无视于这一条直线究竟有多长。注意A与B′的封闭性，封闭性是二元运算中不可或缺的必要条件（有“反”元素及吻合结合律），结合律又衍生到分配律，分配律攸关质能的分配与转变。进而跨入拓扑转换与克莱恩（Felix Klein，1849—1925）就职演说与书面论文《爱兰根大纲》（ErlangerProgramm，1872）［16］，以《群论》为基础重述几何学的定义。

6 结论

如此一来，可以重新定义一套不连续的数字：“Billy’s number”，其实 “Billy’s number”并不稀奇，它就是在荧光幕上所看见的数字化数字（pixel），建立的方法也是当年普利克建立坐标相同的手法。此外，挪威逻辑学家史克莱姆（Thoraff Skolem）也曾从逻辑与集合论的观点提出这一方面的研究成果。

数学史揭示，从古希腊迄今数学曾经出现过三次基础危机。每次危机皆是由于数学发展出新工具，应用的领域极速扩展，导致原本数学基础的坚实性出现裂痕，以至于理论不能为应用提供发展方向与证明，而应用反而动摇了理论的根基。随着时间的推移，矛盾越来越多，问题也越来越明显，令人们终于意识到数学理论的基础原来是建立在沙滩上。所以每一次危机，总有一大部分不适用的理论被迫改造与放弃。说来令人难以置信，这三次基础危机并未渡过，并且延续了下来，这就是千百年来数学悬而未解问题的肇因。

“Een schip op het strand is een baken in zee.”（Dutch proverb）

沙滩上的船骸，是大海的灯塔。（他山之石，可以攻错。）（A ship on the beach is a lighthouse to the sea.）

“鉴古而知今”是人类之所以能够在地球芸芸众生中峥嵘头角脱颖而出的原因。当回顾数学史时，可看到以下这些事实：莱布尼茨（Gottfrid Wilhelm Leibniz）是第一个踏在连续与离散之间的人，19世纪毕达哥拉斯派（Pythagorean brotherhood）学者德国柏林大学数学教授克罗尼克（Leopold Kronecker）是第一个踏入离散数学门扉的人。至于本文则是第一篇剔除了现代分析之父魏尔斯特拉斯（Weierstrass Karl T.W.）的函数极限“ε－δdefinition”定义，给出离散数字的定义，为数字、原子与时空结构划上等号，将古典物理及量子力学与数学及混沌理论整合起来的论文。

克罗尼克在宴会中，曾经语重心长地举杯致词［4］：

只有自然数来自上帝，其他一切皆是人为。

“Die ganze Zahlen hat Gott gemacht，alles andere ist Menschenweck.”

“God made the whole numbers，all the rest is the work of man.”

据悉莱布尼茨曾经有感而发，说了一句俏皮话［4］：

“The principle of pure d-ism，as opposed to the dot-age of university.”（大自然的原则对照大学中的老耄。）

话中的 “pure d-ism，deism”是双关语，将大自然的原则对照于神谕（oracle）。

如今根据电脑时代中的观点，将莱布尼茨的俏皮话改为：

“The fundamental principle of universe as opposed to the dot of computer-age.”（宇宙中的基本原则对照于电脑时代中的点。）

拉普拉斯（Pierre Simon Laplace）评述［16］：

莱布尼茨相信他已在“2”进制中看到了上帝创造万物，在那里只有“0”与“1”，“0”代表虚无，“1”代表上帝。

“2”进制数字是电脑中采取的数字，亦是布林代数（Boolean algebra）中的数字，相当于欧几里德几何学中没有大小的点。无疑它们仅是 “Billy’s number”中的一个小小部分，亦可对照于西元前五世纪学者琉希帕斯（Leucippus）及他的弟子德谟克利特（Democritus）提出的原子：一种均匀坚硬，既不可改变又不可分割的物体。原子有不同的大小与形状（也就是拓扑性）。

近百年来，物理学迈入钻牛角尖的危机，但这情况又因为混沌理论与电脑模拟戏剧化地出现了转机。相对论剔除掉了欧几里德几何学中的平行公设，量子力学推翻了牛顿力学中的连续性，混沌理论与电脑模拟又戏剧化地凸显了毕达哥拉斯无理数不存在的论点。

然而这些问题“悬而未解”却以讹传讹，以至于又衍生出后续的种种问题。

若用 “Billy’s number”取代目前数学中连续性的数字，由于它同时具有caridinal set与ordinal set及时间与空间的维度，与拓扑性及代数性特质。它的数列稠密而不连续，它的元素是离散的，既没有无理数，也没有超越数，因此彻底消弭了数学史上三次的基础危机。它那些显而易见的特质，剔除掉了一切不能具体化的东西。它消弭了微积分、抚平了牛顿力学与量子力学间的伤痕，除掉了笛卡尔坐标、解析几何之类与不吻合事实，或不能具体化的东西，带领着我们跨越数学与物理间的知识鸿沟，并为数学打开了通往物理公设化的门扉，从根本上整合了大自然中所有的知识。

此证（Quod Erat Demonstrandum）。

（2012年4月19日收到）

［1］The lst International Congress of Mathematicians ［C］.Zürich，1897.

［2］International Congress of Mathematicians［C］.Paris，1900.

［3］RIDDLE L.Department of Mathematics，Agnes Scott College，http：／／people.bath.ac.uk／cs3mmh／ifs.

［4］EVES H W，EVES J H.An introduction to the history of mathematics［M］.6th ed.Philadelphia：Saunders College Pub.，1990.

［5］ROSE P L.The Italian renaissance of mathematics［M］.Geneva：Librairie Droz，1975.

［6］RUFFINI P.Teoria generale della equazioni［M］.1799.

［7］ABEL N H.Journal für die riene und angewandte Mathematik，1826.（known as Crelle’s Journal）

［8］GRAY J J.The Hilbert challenge［M］.胡守仁，译，2000.

［9］BLATER D.The Joy ofπ［M］.洪万生，译本导读，1999.

［10］HEATH T L.The thirteen books Euclid’s elements［M］.蓝纪正，朱恩宽，译.1999（第九卷，命题三十五）：281.

［11］模糊数学入门［M］.台北：九章出版社，1996.

［12］http：／／www.facstaff.bucknell.edu／udaepp／090／w3／toddw.htm.

［13］FRALEIGH J B.A first course in abstract algebra［M］.Boston：Addison-Wesley，1967：203-205.

［14］RICHARDS J A，JR SEAR F W，WEHR M R，et al.Modern collage physics［M］.1962：395-403.

［15］FRALEIGH J B.A first course in abstract algebra［M］.Boston：Addison-Wesley，1967.

［16］LAPLACE P S.Essai philosoque sue les probabilites（概率哲学探究）［M］.5th ed.Cambridge：Cambridge University Press，2009.

Modeling and Simulation of Complex Earth System for Climate Change（Part II）

CHA Billy①，LI Qi②
① ②Professor，CyberGISStudio，PekingUniversity，Beijing100871，China

There is an unwritten rule in science，indicates that physics is a concrete model and the primitive terms are objects and relations adapted from the real world.But，mathematics is an ideal model，that the primitive terms are objects and relations adapted from some other postulation development.Their characters are naturally different.As a result，physicists use observations，measurements，and experiments argue for these phenomena they found.While，mathematicians use deduction debate for their noumenas，the former is physical description，and the latter is the fact of substance.Trivial，this two kind knowledge have themselves inherent incompletion，and there is inconsistency trouble with them at the very initial stage，which continuous unlimited among their descendant subjects.Thus，those unsolved problems arise.For this reason，in this article，we base on the truth and through geometric structure of time-space and nature laws in universe which they followed，let the physics and mathematics consistency，and then those unsolved problems can be accomplished.Further for that，revealed a way to the axiomatisation of physics，eliminate the profoundly disturbing crises wherein the foundation of mathematics.

axiomatisation，chaos，nonlinear，discontinuity，butterfly effect，attractor

10.3969／j.issn.0253-9608.2012.06.002

（编辑：方守狮）