求解旅行商问题的一种新方法
2012-08-16吕善国曹义亲陈红丽
吕善国,曹义亲,陈红丽
(华东交通大学软件学院,江西南昌330013)
旅行商问题[1](traveling salesman problems,TSP)是一个经典的组合优化问题,是指在给定了距离的城市集合中求解经过所有城市恰好一次的最短回路,是一个典型的NP难问题[2]。在VLSI芯片设计、机器人控制和车辆选路等许多领域有广泛的应用[3]。
求解该类问题可以使用精确算法,常用的方法包括:分枝定界法[4]、线性规划法[5]和动态规划法[6]等,能保证得到最优解,但计算复杂度随着网络规模的增大呈指数增长,是NP困难的。当网络达到一定规模时,通常使用近似算法或启发式算法求解TSP。近似算法是把误差控制在一定范围的前提下快速得到解决方案,包括构造型算法和改进型算法。构造型算法从某个非法解开始,按一定规则一次性的构造一个合法解;而改进型算法在给定的初始合法解上逐步改进,是一种迭代法。近似算法主要有遗传算法[7]、蚁群算法[8]、模拟退火算法[9]、人工神经网络[10]、LK算法[11]、人工免疫算法[12]、粒子群优化算法[13]和混合智能算法[14]等。
因此,寻找一种高效的近似算法来求解旅行商问题意义非常重大。通过对旅行商问题的深入研究,本文提出了一种简化模型法SModel(simple model)来求解旅行商问题。SModel方法在简化的网络模型基础上,对模型中的路径进行重构得到旅行商问题的解。
1 简化网络的模型
1.1 符号定义
在对具体问题进行描述之前,先给出一些符号的定义。对于给定的图G=(V,E,W),其中:V为顶点集合,V={v i,i=1,…,n},E为边的集合,W为边的权值集合。D(vi)和SD(vi)均表示节点vi的度,包括节点的入度和出度,区别在于D(vi)表示初始网络中节点vi的度,而SD(vi)表示被处理过的网络中节点vi的度;路径表示从一个节点出发经历一系列节点最终到达某个节点的通路,两个端节点的度为1,其余节点的度均为2;环路表示从一个节点出发经历一系列节点最终回到出发点的路径,环路中所有节点的度均为2。
1.2 简化模型
简化初始图的模型在一定的约束条件下把一个初始图简化为边的数量较少的图,在简化网络图的基础上,进行路径的选择,构建满足要求的路径。简化模型记为SModel,其详细过程包括排序操作和选择操作。
1)排序操作。对于一个图G=(V,E,W),把E中所有边按照权值从大到小排列,排序后的边存储在一个集合SortEdgeArray中。
2)选择操作。所有排序后的边按照先后顺序进行测试。对于任一条边 <vi,vj>,如果满足式(1)的限制,<vi,vj>将从SortEdgeArray中删除,同时,D(vi)和D(vj)都将减1。

当所有的边都经过测试后,剩下的边与所有的节点可以构成一个或多个子图,子图中绝大多数节点的度都为2,很少一部分节点的度为3或者更大的数字。构建SModel的计算复杂度为O(eln(e))(其中,e为边的数目)。
2 模型法求解TSP
初始图转化为SModel后,将对SModel中的节点和边进行一次遍历。所有节点和边的初始状态置为0,一旦被遍历过了,状态由0转化为1。
起始节点在度数大于2的节点中随机选择,记为vr。遍历结点vr,状态由0变为1;在状态为0的边集和结点集中选择与vr相连的边erj和邻接点vj,且边erj状态由0变为1;将vj作为vr,重复上述过程,直到所有结点均被遍历过或者找不到状态为0的结点vr的邻接点为止。
如果未遍历完成且找不到状态为0的结点vr的邻接点,说明发现了一个局部环。在整个遍历过程中,可能存在大量的局部环。经分析,所有的局部环分为两类,分别处理这两类局部环。
2.1 处理局部环
2.1.1 只有1个结点的度大于2的局部环
遍历过程中发现局部环,若如图1(a)所示,所有结点中只有1个结点的度大于2,这种类型的环称为Cycle1。在该环中,只有与结点vs相连的边大于2,因此需要删除一条与vs相连的边。对应Cycle1,破环方法如图2(b,c,d)所示。
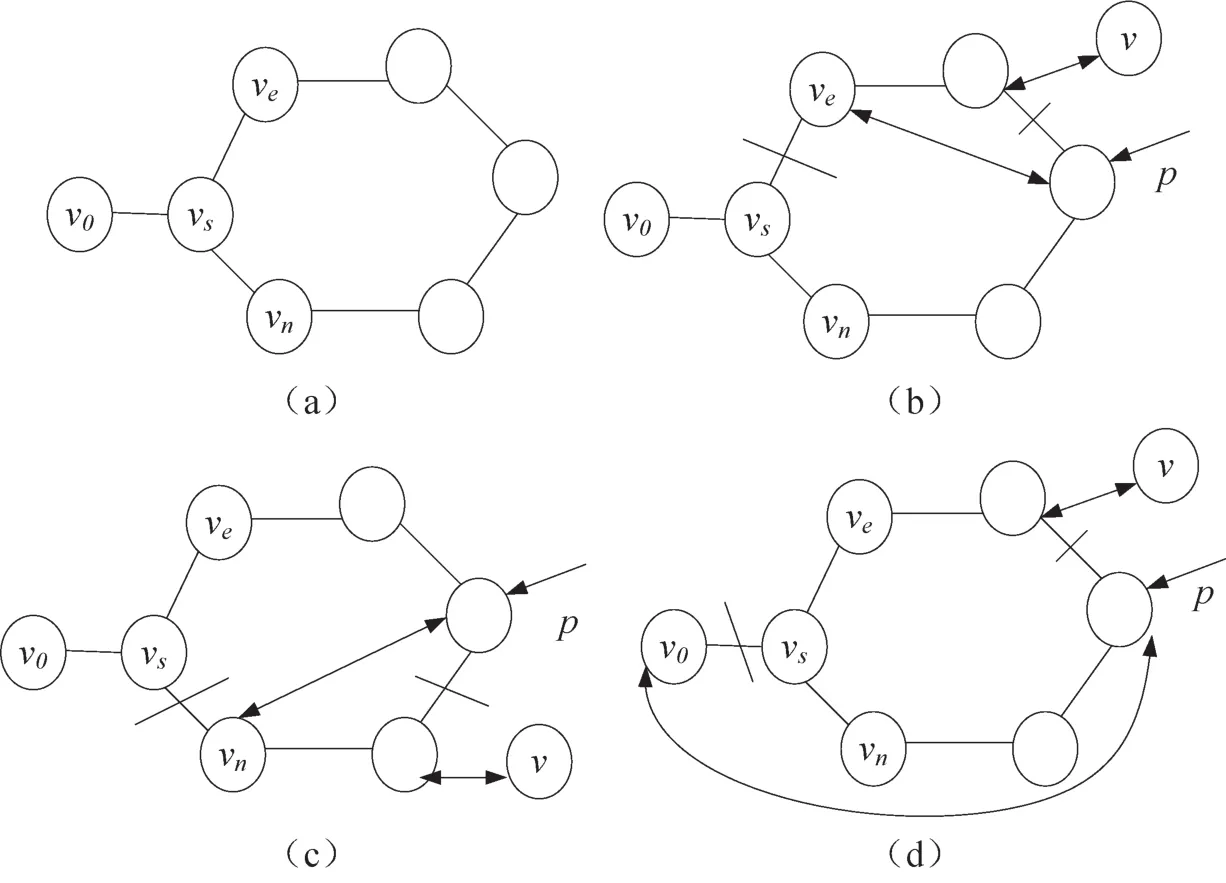
图1 Cycle1的破环方法Fig.1 The broken ring methods of Cycle1
ve作为这个局部环中最后被遍历的节点,vn标记为仅次于vs被遍历到的节点。对于图1(b),如果ve与环中的某节点(p指针指向的节点)在初始图中是相连的,同时,沿着遍历方向的下一个节点与某个状态为0的节点在初始图中也相连,则可以删除p指针指向的节点与其下一个节点之间的连边和边 <ve,vs>,并加入新边连接到状态为0的结点v,新加入的边状态由0变为1,当前节点变为新加入的节点,继续遍历;图1(c)与图1(b)的处理方法相似,把ve变为vn,p指向节点的下一个结点按照逆遍历方向选择。如果仍然不能破坏局部环,就考虑图1(d)所示的方法来解决。图1(d)中,v0先于vs被遍历。如果v0与此环中某节点在初始图中相连,同时在p指向节点的遍历方向的下一个节点与其他状态为0的节点在初始图中也相连,则新加入的状态为0的节点变为当前节点,新加入的边状态由0变为1,继续遍历。
选择状态为0的新节点时要满足总代价增量最小的原则,即增加的两条边的权值和与删除的两条边的权值和的差值最小。
2.1.2 多于1个节点的度大于2的局部环
相对于类型Cycle1,局部环中度大于2的节点数目多于1个的环称为类型Cycle2。在考虑结点之间是否可以连接时,首先计算度数大于2的结点,其破环方法与Cycle1的破环方法类似。
不管是哪种类型的局部环,如果其无法与其他状态为0的节点相连,则把本次遍历路径中的所有节点和边存储到一个路径集中,重新选择下一次遍历的初始节点。
2.2 对集中路径的连接和调节
当SModel遍历完成,路径集中的路径数目通常大于1。如果不同路径中的端节点是可连接的,则这两条路径可以连接为一条路径。连接方法如图2(a,b)所示,节点va,vn,vi和vk都是不同路径中的端节点,对于图2(a),如果某路径的一个端节点与另一条路径中的中间节点(图2(a)中为vc)是可连接的,而此中间节点的邻居节点(图2(a)中为vb)与其另一端的端节点vn是相连的,则这两条路径可以合并为一条路径。对于图2(b),如果一条路径的两个端节点与另一条路径中相邻的两个节点分别相连(vi与vc相连,vk与vd相连,vi和vk是一条路径的两个端点,vc和vd在另一条路径中相邻),则这两条路径可以合并为一条。
重复上面的操作,直到所有路径合并为一条,称其为全局路径。
2.3 生成全局环
如图2(c)所示,vb与vc为邻居节点,vb与端点va在同一侧,vc与vk也在同一侧,如果一对邻居节点分别与不同侧的端节点相连,则全局路径可以转换为全局环。例如,vc与va相连,vb与vk相连,增加边<vb,vk> ,<va,vc> ,删除边 <vb,vc> ,则完成所有操作。增加和删除边的操作要遵循最小增量原则。
3 实验分析
求解TSP问题的近似算法性能标准包括算法的运行时间和解的质量。通常以相对于最优解的误差为评价标准,计算公式如下

式中:R为解,Opt为最优解。
以下给出在TSPLIB[15]的典型实例上进行的测试结果,如表1所示。实例名称中的数字表示实例的规模,如实例Eil51的规模为51。Opt是TSPLIB中的最优解,即最短路径值Min即最短路径是简化模型法的最优解与Opt的误差,Avg是简化模型法的平均解与Opt的误差,n是遍历过程中发现的局部环数目。
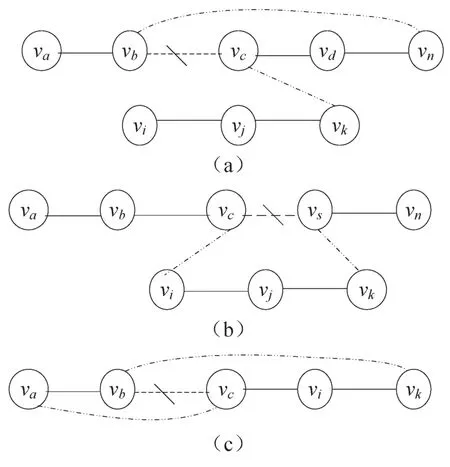
图2 处理路径的方法Fig.2 The method of dealing with path

表1 各实例测试结果Tab.1 Test results of examples
实验中每个实例至少运行100次,从实验结果看出,测试实例的平均解与最优解非常接近,这是由于从全局入手来构造SModel,避免了陷入局部最优的状态。另外,简化模型法得到的最优解与TSPLIB中的最优解的误差基本都小于10%,是可以接受的。值得注意的是,局部环的数目在一定程度上可以表示简化模型法的计算复杂度。
简化模型法解决TSP问题的时耗小。实验中,对节点规模为1 000到5 000个节点的随机网络图进行了处理,其运行时间与节点规模的关系如图3所示。显然,随着节点规模的增加,运行时间也会增加,但是增长程度与线性曲线接近。

图3 节点规模为1 000到5 000的时间消耗Fig.3 Time consumption from 1 000 to 5 000 nodes
4 总结
本文提出了一种求解旅行商问题的新方法。新算法对初始网络进行简化得到简化模型(SModel),然后处理模型中的局部环,删除冗余的边,生成多条路径,再对生成的路径进行重构,最终得到满足要求的全局环路。在TSPLIB中典型实例上的实验结果表明,该算法在求解速度和求解能力方面都能得到比较令人满意的结果。
[1]LAWLER E L,LENSTRA J K,RINNOOY KAN A H G,et al.The traveling salesman problem[M].Chichester:John Wiley&Sons,1985:51-78.
[2]GAREY M R,JOHNSON D S.Computers and intractability:a guide to the theory of NP-Completeness[M].San Francisco:W H Freeman,1979:25-30.
[3]万颖瑜,周智,陈国良,等.SizeScale:求解旅行商问题(TSP)的新算法[J].计算机研究与发展,2002,39(10):1294-1302.
[4] CARPANETO G,TOTH P.Some new branching and bounding criteria for the asymmetric traveling salesman problem[J].Management Science,1980,26(7):736-743.
[5]G DANTZIG,R FULKERSON,S JOHNSON.Solution of a large scale traveling salesman problem[J].Operations Research,1954,2(4):393-410.
[6]BELLMAN R.Dynamic programming treatment of the traveling salesman problem[J].JACM,1962(9):61-63.
[7]SU F,ZHU F,YIN Z,et al.New crossover operator of genetic algorithms for the TSP[C]//Yu lean.International Joint Conference on Computational Sciences and Optimization.Jinan,China:IEEE Computer Society,2009:666-669.
[8] ZHOU Y.Runtime Analysis of an ant colony optimization algorithm for TSP instances[J].IEEE Transactions on Evolutionary Computation,2009,13(5):1083-1092.
[9]SONG C,LEE K.Extended simulated annealing for augmented TSP and multi-salesmen TSP[C]//Don Wunsch,Michael Hasselmo,et al.Proceedings of the International Joint Conference on Neural Networks.Portland,Oregon:IEEE Neural Networks Society,2003:2340-2343.
[10] ABDEL-MOETTY S.Traveling salesman problem using neural network techniques[C]//Ahmed Zoweil,Dokki,Giza.The 7th International Conference on Informatics and Systems.Cairo,Egypt:IEEE Conference Publications Program,2010:1-6.
[11]LIN S,KERNIGHAN B.An effective heuristic algorithm for the traveling salesman problem[J].Operation Research,1973,21(2):486-515.
[12] HUNT J,COOKE D.Learning using an artificial immune system[J].Journal of Network and Computer Applications,1996,19(2):189-212.
[13]JAMES K,EBERHART R.Adiscrete binary version of the particle swarm algorithm[J].Proceeding of the IEEE International Conference on Systems,Man and Cybernetics,1997(5):4104-4108.
[14]陈冬华.旅行商问题推广及其混合智能算法[J].华东交通大学学报,2011,28(2):102-106.
[15]REINELT G,TSPLIB.Atravelling salesman problem library[J].ORSAJournal of Computer,1991,3(4):376-384.
